Условие ортонормированности

Получим постоянную из условия нормировки вероятности

.

С учетом вещественности и получаем

.

С учетом (П.3.7)

,

выполняется

.

Полагаем

,

получаем

,

где x – безразмерная координата,

. (6.33)

Учитывая ,,, из (6.32) находимосновное состояние, имеющее наименьшую энергию :

, (6.33а)

и первое возбужденное состояние с энергией

. (6.33б)

В точках поворота классический осциллятор с полной энергиейостанавливается

.

Получаем точки поворота классического движения с энергией

, ,,,

показанные на рисунке большими точками. В квантовой механике решения существуют за пределами областей, доступных классической частице. Это явление называется туннельным эффектом.

Рекуррентные соотношения

• Рекуррентное соотношение для полиномов Эрмита (6.15)

умножаем на и учитываем

, ,,

для (6.32)

.

выполняется

. (6.34)

Полученное соотношение позволяет устранить множитель x перед функцией .

• Функцию (6.32)

дифференцируем

.

Учитываем (6.12)

, ,

получаем

. (6.35)

Соотношение устраняет дифференцирование функции .Из (6.35) следует

, (6.36)

где

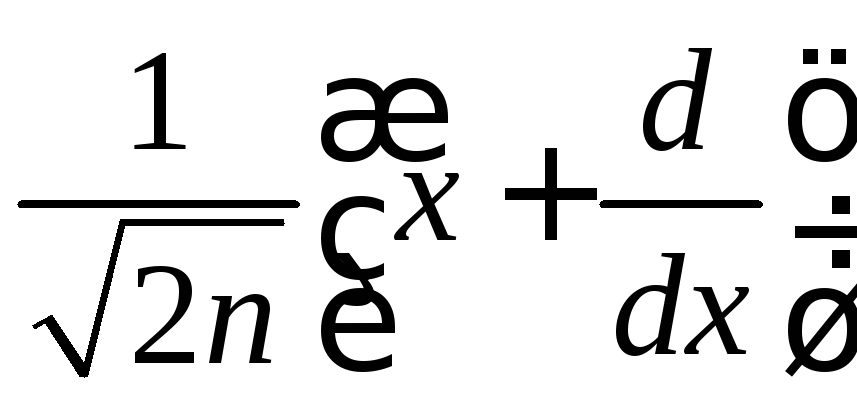–оператор уничтожения кванта энергии .

• Из (6.34)

выражаем

.

Подстановка в (6.35) дает

. (6.37)

Из (6.37) находим

, (6.38)

где

–оператор рождения кванта энергии .

• Суммирование (6.35) и (6.37) дает

. (6.39)

Соотношение используется в многочисленных задачах, где вычисляются матричные элементы.

Матрица перехода между состояниями системы

Множество возможных состояний системы описывается ортонормированным базисом функций . Внешнее возмущение, действующее на систему, выражается оператором . ВозмущениеF переводит систему из состояния в состояние

.

Множество состояний системы и мера воздействия на них описываются матрицами

, , .

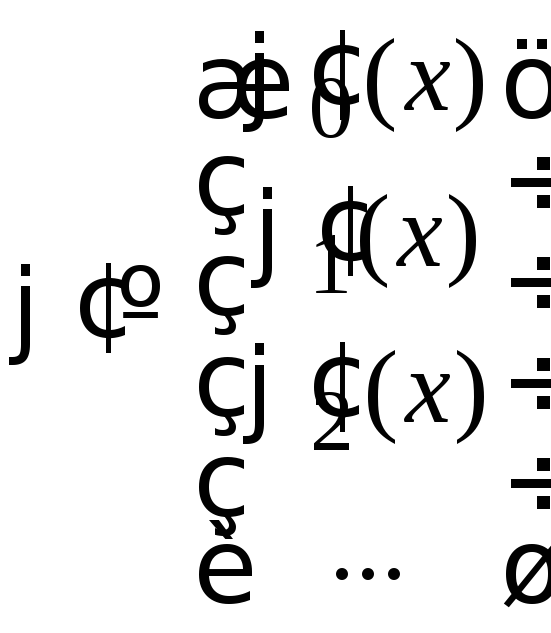Матричный элемент

Матричный элемент экспериментально измерим, и выражает вероятность перехода системы между состояниямипод действие оператора. По индексам переход происходитсправа налево, k – начальное состояние, n – конечное состояние.

В пространстве функций с базисом и весовой функциейматричный элемент оператора между ортамииопределяется в виде скалярного произведения

, (1)

где A, B, – вещественные.

Физический смысл матричного элемента

Диагональный матричный элемент

есть среднее значение величины f, описываемой оператором , в состоянии .

Недиагональный матричный элемент

есть амплитуда вероятности перехода между состояниями под действием оператора.

Вероятность перехода равна

.

Операторы координаты и импульса

,

.

Эрмитовый оператор

Любой физический оператор является эрмитовым

, (2)

где «+» – операция эрмитового сопряжения. Это условие обеспечивает вещественность собственных значений оператора, т. е. результатов измерения соответствующей физической величины. Эрмитового сопряженный оператор определяется в виде

,

.

Эрмитовый оператор можно переносить в скалярном произведении функций от одного сомножителя к другому

,

. (3)