Интегралы с полиномами Эрмита

1. Вычисляем

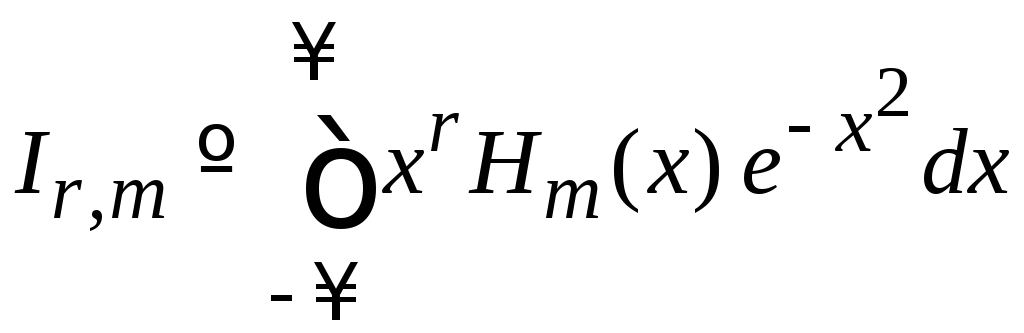
Учитываем четность (6.3)

.

Если – нечетное, тогда

.

Если – четное, то в подставляем форму Родрига (6.2)

.

Интегрируем по частям m раз, свободные слагаемые зануляются

= ,

учтено

.

Используем (4.9)

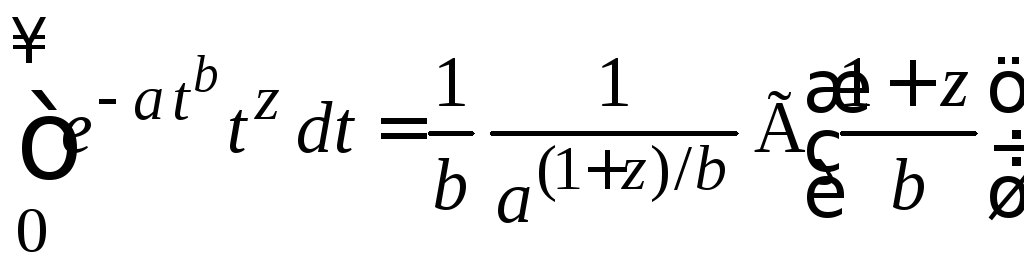
при ,,и находим

.

Учитываем (4.11)

,

тогда

.

В результате

, – четное. (6.21)

Частные случаи:

Из (6.21) при с учетомполучаем

, (6.21а)

Из (6.21) при

, (6.22)

Из (6.22) при инаходим

, (6.23)

. (6.24)

В формуле (6.22)

,

заменяем , где. Преобразуем правую сторону

.

Для гамма-функций вблизи полюсов используем (4.4) в виде

.

При , ,, получаем

.

В результате (6.22)

при дает

, . (6.25)

Из (6.25) при иполучаем

, (6.26)

. (6.27)

2. Вычисляем

,

Для используем полиномиальную форму (6.4)

,

интеграл сводится к предыдущему типу

.

Используем (6.22)

, ,

при

.

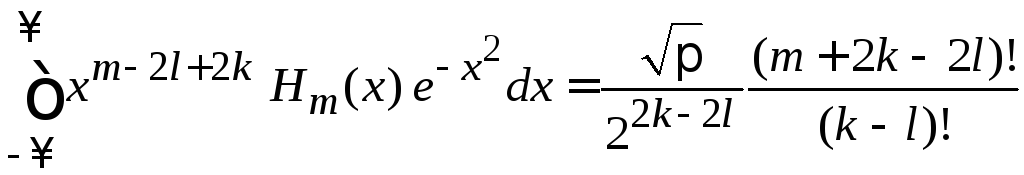В результате

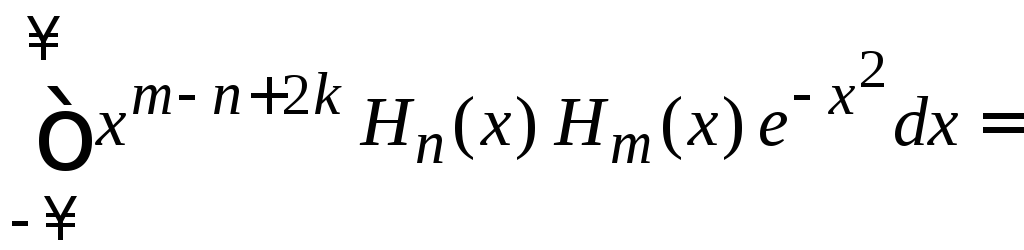
=, (6.28)

где знаменатели с факториалами ограничивают .

Частные случаи:

При ,из (6.28) получаем нормировку полиномов Эрмита

, (6.29)

что подтверждает результат, полученный методом факторизации.

При ,и при,из (6.28) находим

,

.

Гармонический осциллятор

От лат. oscillatio – «качание». Система колеблется по гармоническому закону.

Осциллятор в классической теории

Шарик массой μ подвешен на упругой пружине в поле тяжести. Трение пренебрежимо мало. При смещении от положения равновесия действует возвращающая упругая сила с коэффициентом жесткостиk. Возникают периодические колебания по оси z.

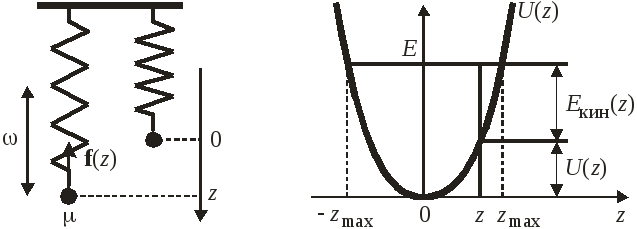
Потенциальная энергия

.

Упругая сила

создает ускорение . Второй закон Ньютона

дает уравнение движения

,

где частота колебаний

, ,

тогда

.

Решение уравнения дает колебания

,

где – амплитуда.

Полная энергия

.

При максимальном смещении

,

тогда

.

Полная энергия зависит от амплитуды колебаний , и может быть любой. Квадрат импульса

(6.30)

Осциллятор в квантовой теории

В квантовой теории спектр энергии эквидистантный

, ,

уровню n сопоставляются n квантов энергии ;

–энергия вакуума.

Уравнение Шредингера

Для стационарной системы используем уравнение Шредингера

.

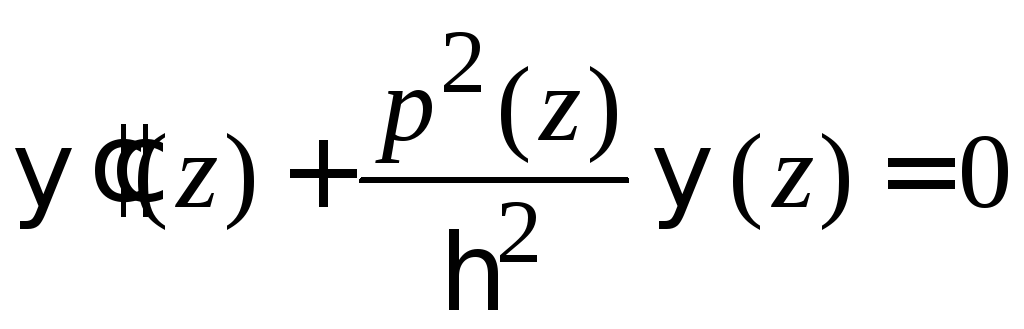Для осциллятора используем (6.30)

,

получаем для состояния уравнение

.

Переходим к безразмерной координате

, ,

, ,

,

Для

,

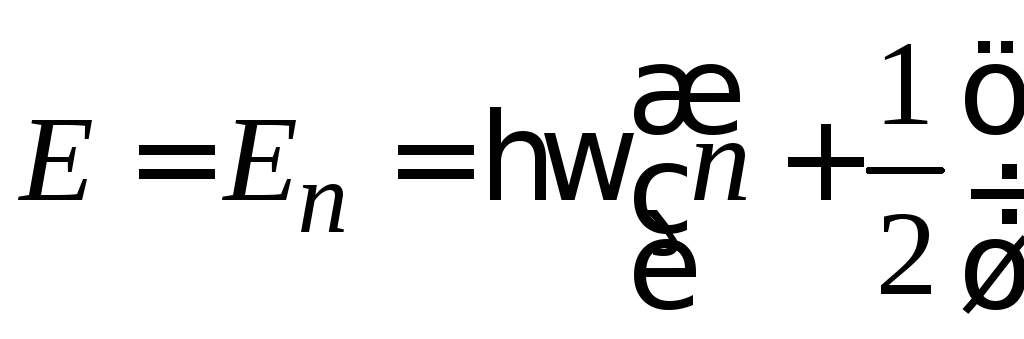с учетом

,

получаем уравнение

, (6.31)

Для этого уравнения методом факторизации ранее получено решение (П.3.6)

. (6.32)

Из (6.3)

и (6.32) находим

.

Четность функции состояния совпадает с четностью номера состояния.

–основное состояние – четное,

–первое возбужденное состояние – нечетное.

Физический смысл функции состояния. Выражение

является плотностью вероятности обнаружения частицы, т.е. вероятностью ее обнаружения в состоянии n в единичном интервале координат около точки z.

Вероятность найти частицу в интервале

.