Тригонометрическое представление
В (6.149) заменяем
,
,
получаем
,
.
(6.150)
Учитывая
четность
,
расширяем область интегрирования до
2π:
,
.
Сравниваем с формулой (1.45)
,
.
из
темы «Преобразование Фурье периодической
функции». Поскольку
– полином степениn
по аргументу
,
то получаем
тригонометрическое
представление
,
,
.
(6.151)
Воспроизводятся результаты (6.148)
,
.
Расширение области определения
Выражение
(6.151) применимо при
.
Метод факторизации не дал ограничения
на область определения. Расширим
первоначально выбранную область до
.
В (6.151)
заменяем
,
.
Используем формулу Эйлера дважды
,
,
получаем
.
Замена
,
дает
.
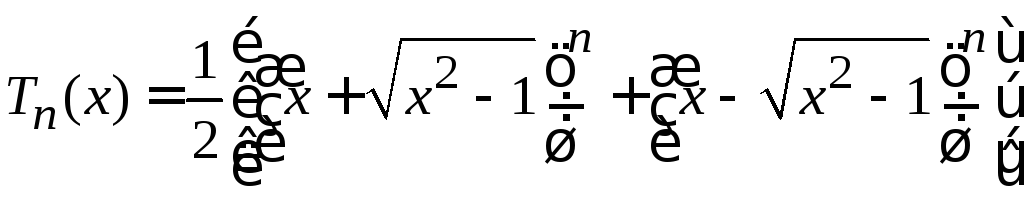(6.153)
Формула
(6.153) применима при
.
Рекуррентные соотношения
1. Используем тригонометрическое равенство
.
В (6.151)
подставляем
,
находим
.
(6.151а)
В результате
.
(6.156)
2.
В (6.156) при
используем
,
получаем
.
(6.157)
3.
В (6.156) при
используем
,
находим
.
(6.158)
Частные значения
Из
,
и (6.157) в виде
при
находим
,
,
,
.
Следовательно,
– порядок полинома
.
Из тригонометрического представления (6.151)
,
находим
,
,
,
.
Геометрическое моделирование
Используем (6.151)
.
1.
На листе высотой 2 и шириной
строим график
.
На рисунке выбрано
.
2.
Сгибаем лист в полуцилиндр радиусом 1,
длиной окружности
.
Осьz,
перпендикулярная образующей, становится
окружностью.
3.
Угловое положение
и координатаz
на цилиндре связаны
.
4.
Рассекаем цилиндр плоскостью, проходящей
через ось цилиндра и точку
.
В плоскости определяем координатуx,
перпендикулярную оси цилиндра, тогда
,
.
5
График
на поверхности цилиндра, спроектированный
на плоскость осевого сечения цилиндра:
является полиномом Чебышева.
Полиномы Чебышева второго рода
,
;
– порядок полинома
Определяем
.
(6.161)
Тригонометрическое представление
Используем (6.151)
,
.
Из (6.161) получаем
.
(6.162)
Рекуррентное соотношение
Используем тригонометрическое соотношение
,
делим
на
,
полагаем
,
учитываем (6.162), и получаем
.
(6.163)
Частные значения
Из
,
,
,
,
и (6.161)
находим
,
.
Из (6.163)
,
получаем
,
.
Уравнение
Уравнение Чебышева (6.146)
-
,
дифференцируем
.
Используем (6.162)
-
,
тогда
,
в результате находим
.
(6.165)
Уравнение относится к гипергеометрическому типу.
Метод факторизации
Стандартное уравнение гипергеометрического типа
-
.
Сравнение дает
,
,
,
,
,
,
,
,
,
,
,
.
Весовая функция
-
,
.
Решение Родрига
дает
.
Полагаем
,
получаем полином Чебышева второго рода
.
(6.166)
Условие ортонормированности
-
,
.
Учитываем
,
,
,
получаем
.
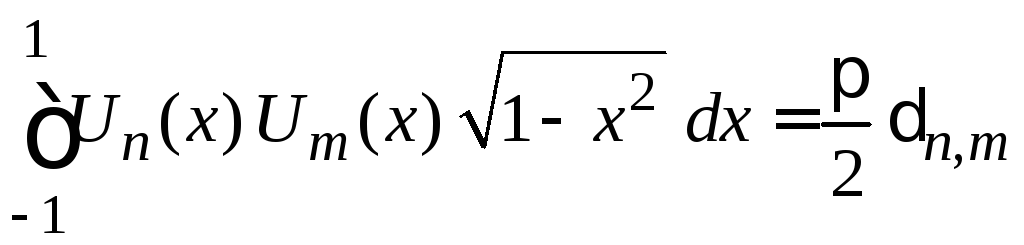(6.167)