Классические ортогональные полиномы

Полином (многочлен) порядка

.

Условие ортогональности

Множество образует базис в гильбертовом пространстве с условием ортонормированности

,

где

–орт;

–скалярное произведение функций;

–весовая функция;

–символ Кронекера.

Классические ортогональные полиномы некоторого типа являются частными решениями дифференциального уравнения обобщенного гипергеометрического типа – полиномы Эрмита, Лагерра, Лежандра, Чебышева, Якоби, Гегенбауэра.

Полиномы Эрмита

, ,

–порядок полинома

Применяются в оптике, в математической статистике, в теории вероятностей, в квантовой механике.

Полиномы исследовали Пафнутий Львович Чебышев в 1859 г. и Шарль Эрмит в 1864 г., они называются также полиномами Чебышева–Эрмита.

Уравнение Эрмита

. (6.1)

Формула Родрига

Методом факторизации получено решение (П.3.3). Доопределяем , тогда

. (6.2)

Весовая функция (П.3.1)

.

Из (6.2) получаем свойство четности

. (6.3)

Полиномы низших степеней

Из (6.2) с учетом

, ,, …

находим

, ,

, ,

, .

Полиномиальная форма

Обобщение частных результатов дает

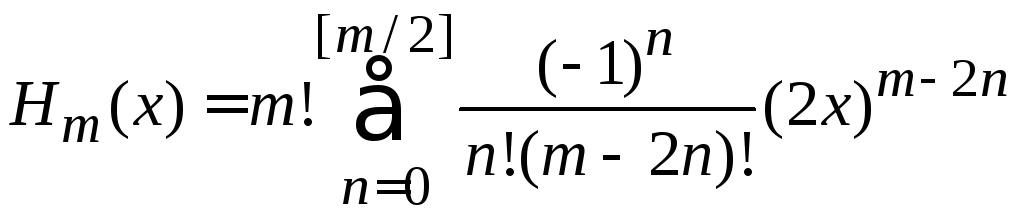, (6.4)

где – целая часть. В частности дляполучаем

Интегральная форма

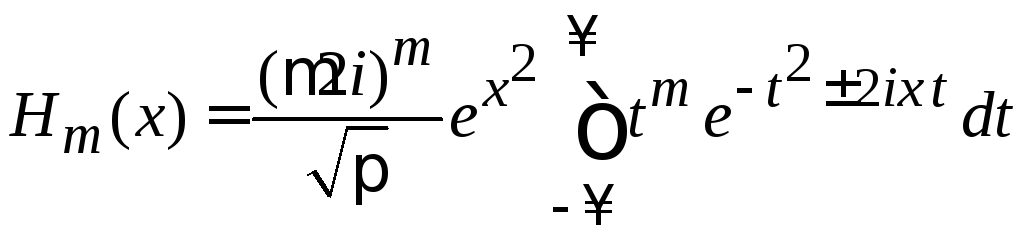(6.8)

применима как для целых положительных m, так и для дробных и для отрицательных m.

Доказательство (6.8):

Используем теорему Фурье о дифференцировании

Для функции Гаусса учитываем (П.2.6)

получаем

.

Под интегралом заменяем :

.

Подстановка в (6.2)

дает

, (6.8)

где комплексное сопряжение не меняет вещественный полином.

Производящая функция

Методом факторизации получена производящая функция (П.3.5)

. (6.10)

Из определения производящей функции (5.14)

с находим ее связь с полиномами Эрмита

. (6.11)

Рекуррентные соотношения для полиномов

Алгоритм получения:

1. Дифференцируем (6.10) по одному из аргументов.

2. В полученное соотношение подставляем (6.11).

3. Приравниваем слагаемые с одинаковыми степенями t.

Соотношение 1 для полинома Эрмита

Дифференцируем по x

, (6.10)

получаем

.

Подставляем (6.11)

,

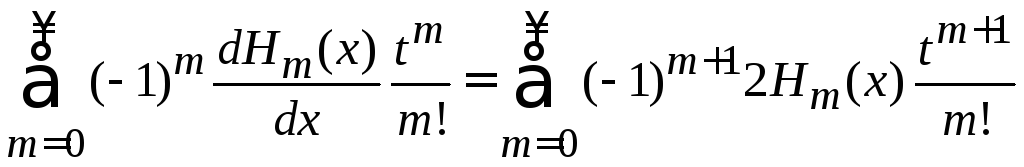приравниваем слагаемые с

,

получаем

, (6.12)

, (6.13)

–оператор понижения порядка полинома.

Соотношение 2

Дифференцируем по t

, (6.10)

получаем

.

Подставляем (6.11)

,

находим

,

приравниваем слагаемые с

,

получаем

. (6.15)

Учет

(6.12)

дает

, (6.16)

–оператор повышения порядка полинома.

Условие ортонормированности

Множество образует базис в гильбертовом пространстве функций, определенных при ,с условием ортонормированности (П.3.4)

. (6.18)

Разложение функции по базису полиномов Эрмита

Если определена при, то она разлагается по базису

. (6.19)

Для нахождения коэффициента :

• умножаем (6.19) на ,

• интегрируем по интервалу ,

• меняем порядок суммирования и интегрирования,

• учитываем ортонормированность (6.18),

• символ Кронекера снимает сумму, оставляя одно слагаемое.

.

Заменяем и получаем коэффициент

.

• Подставляем полином в форме Родрига (6.2)

,

получаем

.

• Интегрируем по частям m раз. Свободные слагаемые зануляются на обоих пределах, получаем коэффициент

. (6.20)