Решение неоднородного уравнения

Для получения решения уравнения

(9.26)

используем интеграл Дюамеля (9.6)

.

Подставляем функцию Грина (9.30)

,

меняем порядок суммирования и интегрирования

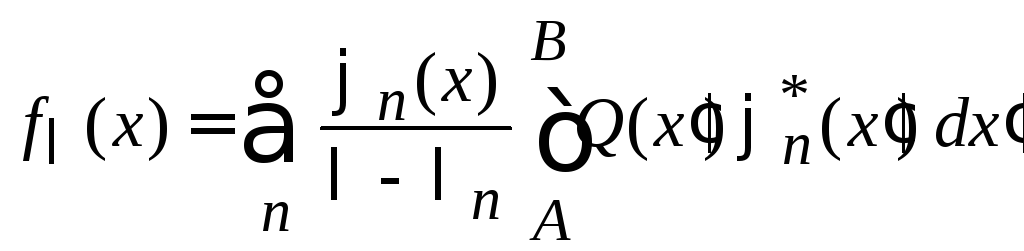. (9.34)

Функцию источника Q(x) разлагаем по базису

, (9.35)

Умножаем (9.35) на , интегрируем по интервалу, меняем порядок суммирования и интегрирования, в правой части используем ортонормированность

,

символ Кронекера снимает сумму

,

и находим спектральный образ источника на частоте

. (9.36)

Подставляем (9.35) в (9.34) и получаем

.

Символ Кронекера снимает одну сумму, и при получаем решение

, (9.37)

где

. (9.38)

Спектральный образ решения на частотеравен произведению образа источникана передаточную функциюна частоте.

Формула (9.37) аналогична разложению функции в ряд Фурье. Выражение (9.38) аналогично теореме Фурье о свертке – образ свертки функций равен произведению образов этих функций. Для спектрального представления аналогом свертки является интеграл Дюамеля (9.6)

. (9.38а)

Неоднородное дифференциальное уравнение описывает действие преобразователя с аппаратной функцией в виде функции Грина , с входящим сигналом в виде возмущенияи с выходящим сигналом в виде решения уравнения.

СпектральноЕ разложениЕ с НепрерывнЫм спектрОм

Теория с непрерывным спектром строится аналогично теории с дискретным спектром.

Если в уравнении Лиувилля

параметры и μ изменяются непрерывно, то множество решений образует непрерывный базисс условием ортонормированности, выраженным через дельта-функцию:

. (9.39)

Доказательство:

Однородное уравнение (9.27), записанное для и для, умножаем слева соответственно наи на

,

.

Взаимно вычитаем равенства, третьи слагаемые переносим направо

.

Интегрируем по интервалу . Граничные условия (9.2)

,

, ,

для левой части дают

.

В результате выполняется

.

1. При получаем ортогональность

.

2. При разлагаем в ряд

, ,

получаем

.

Сравниваем

с равенством (2.4)

.

Для нормированных функций получаем (9.39)

.

Разложение функции Грина

В выражении (9.30) для дискретного спектра

заменяем

, ,

где – непрерывная величина. Сумма переходит в интеграл

, (9.40)

где

(9.41)

– передаточная функция на частоте . Для запаздывающей функции

, . (9.41а)

Разложение функции источника (9.35)

получает вид

, (9.42)

где –спектральный образ источника на частоте .

Подставляем (9.40) и (9.42) в интеграл Дюамеля (9.38а)

.

Меняем порядок интегрирований

,

учитываем ортонормированность (9.39)

,

и фильтрующее свойство дельта-функции, получаем

, (9.43)

где

. (9.44)

Спектральный образ решения на частоте равен произведению образа источника на передаточную функциюна частоте. Результат аналогичен формуле (9.38) для системы с дискретным спектром.