Гармоническое возмущение однородной системы

Гармоническое возмущение с частотой и амплитудойA имеет вид

.

Для Фурье-образа находим

.

Из (9.11) получаем состояние возмущенной системы

. (9.12)

При гармоническом возмущении однородная система совершает вынужденное колебание с частотой возмущения и с амплитудой, равной произведению амплитуды возмущения на частотную передаточную функцию.

Метод спектрального разложения для уравнения лиувилля

Уравнение с постоянными коэффициентами и неограниченной на вещественной оси областью определения описывает однородную систему и решается методом Фурье-преобразования, т. е. путем разложения уравнения по базису гармонических функций.

Если коэффициенты уравнения являются функциями , где, и/или область определения конечная, то используется метод спектрального разложения, обобщающий метод Фурье. Разложение ведется по ортонормированному базису функций, удовлетворяющих однородному уравнению.

Рассмотрим метод применительно к уравнению Лиувилля

, (9.27)

где ;– вещественные. Число называется собственным значением, частное решение –собственной функцией. Множество считаем известным.

Дискретный спектр

В гильбертовом пространстве функций с областью определения частные решения уравнений (9.27), отличающихся числом, образуют базис с условием ортонормированности

. (9.28)

Доказательство:

Уравнение (9.27) записываем для и, и умножаем слева соответственно наи:

,

.

Равенства взаимно вычитаем, третьи слагаемые переносим направо

.

Интегрируем по области определения . Для левой стороны получаем

.

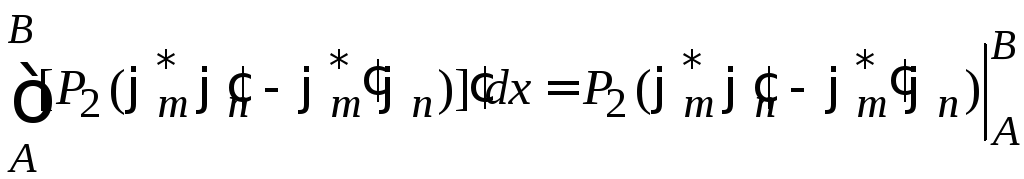Граничные условия (9.2) в точках A и B

,

,

где ;– вещественные, дают

,

.

В результате

.

При , получаем ортогональность функций базиса

, .

С учетом нормировки функций за счет постоянных множителей, получаем (9.28).

Разложение функции Грина

Функция Грина удовлетворяет уравнению

. (9.25)

Разлагаем функцию по базису

. (9.29)

Для нахождения коэффициента подставляем (9.29) в (9.25)

.

Учитываем (9.27)

,

получаем

.

Умножаем равенство на , интегрируем поx от A до B, переставляем суммирование и интегрирование

.

Для правой стороны равенства используем фильтрующее свойство дельта-функции, для левой стороны – ортонормированность (9.28)

.

Получаем

.

За счет символа Кронекера в сумме остается одно слагаемое

.

Заменяем и находим коэффициент

.

Результат подставляем в (9.29)

,

и при находимспектральное разложение функции Грина

, (9.30)

где

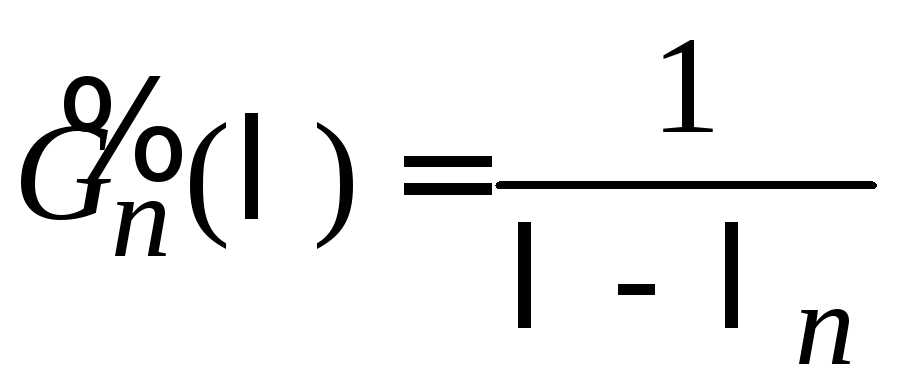(9.31)

– спектральный образ функции Грина, или передаточная функция на частоте .

При вещественном из (9.30) получаемсоотношение взаимности

. (9.32)

Следовательно, комплексное сопряжение меняет местами причину и следствие, т. е. обращает течение времени. Этот вывод был ранее сделан при анализе матричных элементов оператора.

При вещественных иполучаем

(9.33)

– причина и следствие перестановочны, т. е. процесс обратимый.