Функция грина однородной системы

Однородной называется система, физические характеристики которой не зависит от выбора начала отсчета аргумента. Такая система описывается дифференциальным уравнением с постоянными коэффициентами и имеет область определения аргумента . Например, стационарная система является однородной по времени.

Сдвиг начала отсчета x не меняет состояния, поэтому функция Грина однородной системы зависит от расстояния между источником возмущения и точкой системы

. (9.7)

Интеграл Дюамеля (9.6) получает вид

. (9.8)

Состояние возмущенной однородной системы является сверткой функции возмущения и функции Грина системы. На языке преобразующего устройства имеем: – выходящий сигнал,– входящий сигнал, и функция Грина–функция преобразователя.

Для функции Грина

,

где ,фурье-образ

(9.9)

называется передаточной функцией системы. Фурье-преобразование уравнения (9.4)

с учетом теоремы Фурье о дифференцировании (1.35)

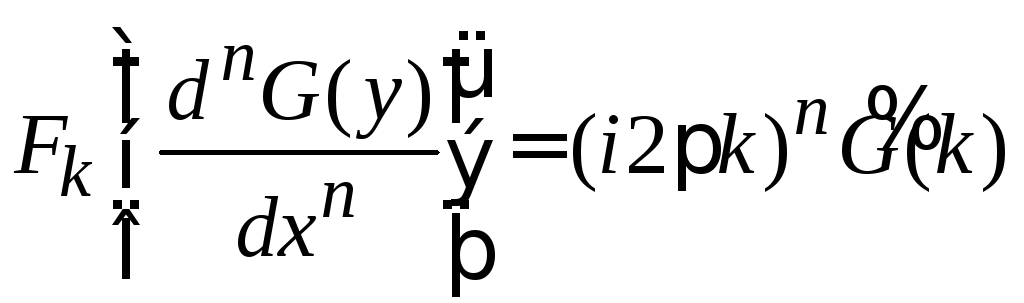
дает

,

откуда находим передаточную функцию

. (9.9а)

Из (9.8) и из теоремы Фурье о свертке получаем

. (9.10)

Фурье-образ состояния возмущенной однородной системы равен произведению фурье-образа возмущения на передаточную функцию системы.

Обратным преобразованием Фурье находим функцию Грина и решение неоднородного уравнения

,

. (9.11)

Нули знаменателя являются полюсами подынтегральной функции. Интеграл вычисляется в общем случае переходом в комплексную плоскость аргумента k и использованием теории вычетов. Результат зависит от пути обхода полюсов, что определяется граничными условиями, накладываемыми на решение при .

Пример

Электрон с энергией и волновым числом в одномерном неограниченном проводникеудовлетворяет уравнению Шредингера , где – волновая функция электрона. Получим функцию Грина.

Система однородная, используем метод Фурье. В (9.9а) и (9.11) подставляем ,,и получаем передаточную функцию системы и функцию Грина

,

,

где

; ;,.

Подынтегральная функция имеет полюса при . Используем теорию вычетов, замыкая контур интегрирования в комплексной плоскости аргументаs. Результат интегрирования зависит от пути обхода полюсов. Возможные контуры интегрирования проходят по вещественной оси и по дуге радиусом R, как показано на рис. 9.2. Доопределяем интеграл, сдвигая полюса заменой , где. На рис. 9.2 полюса обозначены звездочками.

а б

Рис. 9.2. Контуры интегрирования

При сходимость интеграла по дуге большого радиусаобеспечивает контур интегрирования на рис. 9.2,а. Во всех точках на дуге выполняется 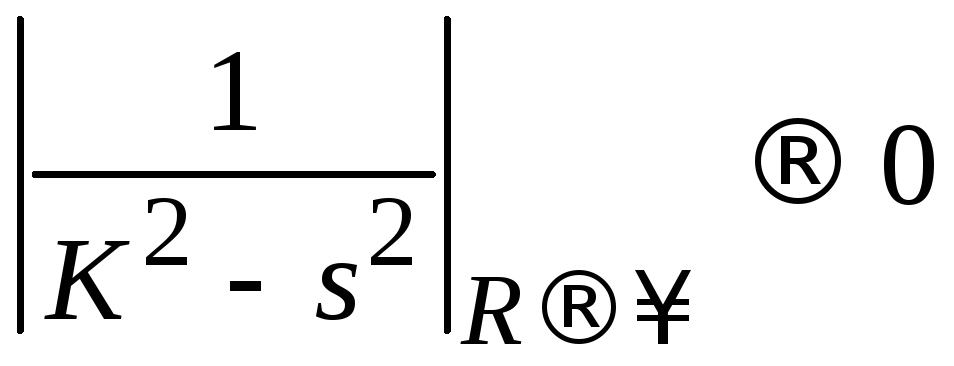, поэтому. Полюсобходится в положительном направлении. Для интеграла по вещественной оси получаем

,

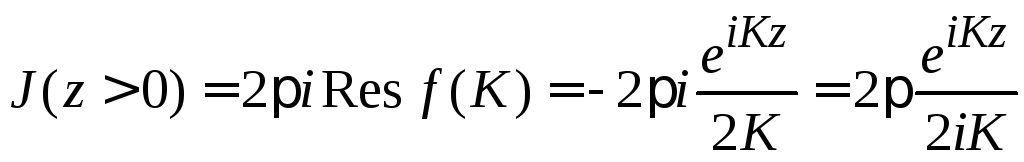где для вычета использовано

.

При сходимость интеграла по дуге обеспечивает контур на рис. 9.2,б, причем . Полюсобходится в отрицательном направлении, тогда

.

Результаты при идля,, объединяет решение

,

,

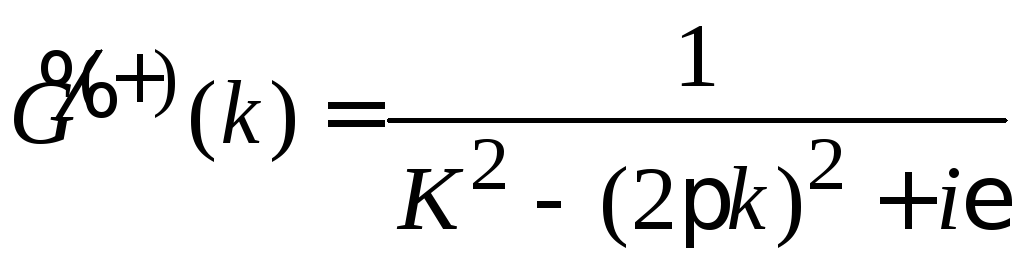, (П.10.2)

где использовано (2.33)

.

Фаза волны (П.10.2) увеличивается, когда точка наблюдения x отодвигается от , следовательно,волна расходится от источника. Выполняется условие излучения Зоммерфельда для запаздывающей волны

.

При замене , где, полюса меняют положения, контуры интегрирования сохраняются. В результате получаем

,

,

. (П.10.3)

Фаза волны (П.10.3) увеличивается при приближении x к , следовательно,волна сходится к источнику. Граничное условие

соответствует опережающей волне.

Выбор соответствует разным граничным условиям при. В природе выполняетсяпринцип причинности и реализуется лишь запаздывающая функция Грина, что соответствует замене волнового числа

, . (П.10.4)

Запаздывающая функция Грина для рассматриваемой системы удовлетворяет условиям сшивания (9.14), (9.15) и уравнению

. (П.10.5)

Действительно, фурье-образ (П.10.5) дает передаточную функцию (П.10.2).

Из (П.10.2) и (П.10.3) следуют размерности ,.При комплексном сопряжении запаздывающая и опережающая функции переходят друг в друга

,

, (П.10.6)

что соответствует обращению времени.

Плотность состояний системы –число состояний в единичном интервале энергии выражается через передаточную функцию системы

. (П.10.7)

Подставляем (П.10.2) и с учетом получаем

.

Плотность состояний соответствует электрону с энергией .