Соотношение между решениями и

Если , то решенияилинейно независимые и связаны соотношением:

. (9.21)

Доказательство:

Используем (9.20а)

,

получаем

.

Интегрируем

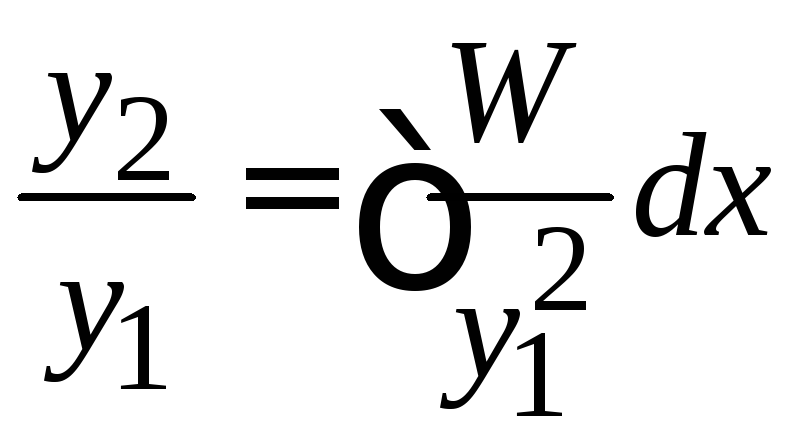
и получаем первое равенство (9.21).

Подставляем (9.20б)

и получаем второе равенство (9.21).

Решение неоднородного уравнения

Для уравнения (9.3)

получено частное решение (9.16)

.

Производные коэффициентов удовлетворяют (9.19)

,

.

Для нахождения ипроинтегрируем (9.19) и устраним произвол выбора постоянных интегрирования путем наложенияграничных условий на концы интервала определения (A, B) аргумента x. В результате решения , и зависят от граничных условий. Рассмотрим частные случаи.

Вариант 1 граничных условий

На область определения решения накладываем условие на в точкеA, на – в точкеB. Произвол в выборе ине должен влиять на решение. С учетом(9.16)

,

получаем

, . (9.21а)

Интегрируем (9.19)

, ,

выбирая пределы, обеспечивающие выполнение (9.21а):

,

.

Находим решение неоднородного уравнения

. (9.22)

Сравниваем (9.22) с интегралом Дюамеля (9.6)

,

получаем

(9.23)

Функция Грина является результатом «сшивания» в точке возмущения x произведений линейно независимых решений однородного уравнения.

Вариант 2 граничных условий

Граничные условия на y₁ и y₂ накладываем в точке B. Точка A не влияет на результаты, если

, .

Из (9.19)

, .

получаем

,

.

Решение (9.16)

сравниваем с интегралом Дюамеля (9.6)

,

и находим

. (9.24)

При получаем.

Если – время, то условиеприозначает выполнениепринципа причинности – реакция системы в момент t не может предшествовать возмущению в момент . Следовательно, вариант 2 граничных условий соответствует выборузапаздывающей функции Грина, отличной от нуля только, если реакция системы происходит позже воздействия на нее.

Уравнение Лиувилля

Если в уравнении

коэффициенты исвязаны соотношением

, (9.24а)

тогда

,

и получаем уравнение Лиувилля

. (9.24б)

Таким уравнением является волновое уравнение Гельмгольца и уравнение Пуассона.

Жозеф Лиувилль (1809–1882)

– французский математик. Исследовал линейные дифференциальные уравнения второго порядка с краевыми условиями – «задачу Штурма–Лиувилля». Построил теорию трансцендентных чисел и эллиптических функций. Доказал «теорему Лиувилля» в механике.

Теорема Грина для уравнения Лиувилля

Для выражения , входящего в (9.19)

, ,

выполняется

(9.24в)

Доказательство:

Подставляем (9.24а)

в (9.20б)

.

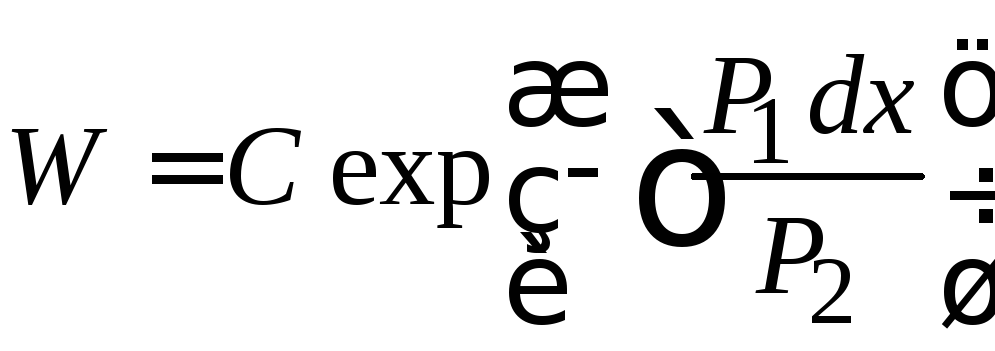С учетом

получаем

.

В результате для варианта 1 граничных условий функция Грина (9.23) и решение неоднородного уравнения (9.22) получают вид

(9.24г)

.

Пример

Струна длиной l закреплена на концах. Колебания в виде поперечных смещений струны с постоянным волновым числомK удовлетворяют уравнению

и граничными условиями

.

Найдем функцию Грина и получим решение возмущенного уравнения

,

где – плотность возмущения.

Рассматриваемая система не является однородной из-за ограниченности размера струны . Для решения задачи используем метод сшивания.

Однородное уравнение имеет общее решение

.

Выбираем два частных линейно независимых решения

,

,

для которых выполняется вариант 1 граничных условий закрепления струны на концах

, .

С учетом

,

,

,

.

получаем

.

Выполняется теорема Грина (9.24в)

.

Из (9.23)

при

, ,

находим

(П.10.1)

Для неоднородного уравнения решение в виде интеграла Дюамеля (9.6)

равно

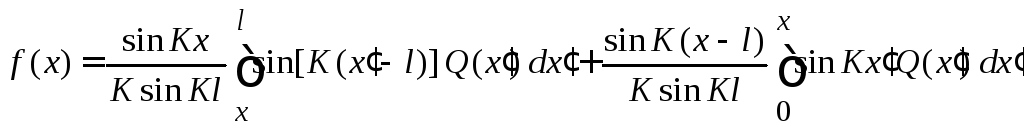
и удовлетворяет граничным условиям закрепленной струны

.

При выполнении

, ,,

на протяжении струны укладывается целое число полуволн, в струне возникает стоячая волна с амплитудой, меняющейся периодически от точки к точке. В этом случае решения однородного уравнения линейно зависимые

, ,

условие применимости метода «сшивания» не выполняется, формула (П.10.1) не применима.