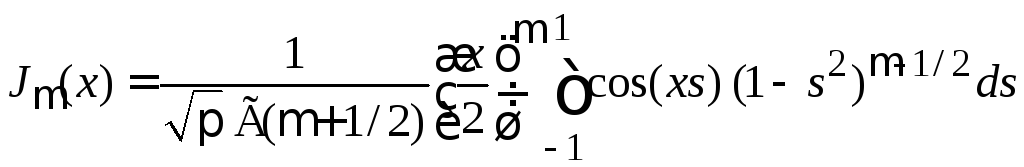Инверсия порядка

Из (8.19)

.

получаем

. (8.22)

Инверсия аргумента

Из интегрального представления Пуассона (8.5)

получаем

. (8.23)

Из (8.22) и (8.23) следует

. (8.25)

Производящая функция

Используем интегральное представление Зоммерфельда (8.16)

,

где

;

.

Разложение в ряд Фурье (1.48)

для плоской волны, движущейся под углом φ к оси x, получает вид

(8.26)

В (8.26) заменяем

, ,

,

находим производящую функцию

. (8.27)

Ряды функций Бесселя

1. В (8.26)

разделяем вещественную и мнимую части

,

.

Учитываем (8.22)

,

и преобразуем слагаемые с

, (8.28)

. (8.29)

При из (8.28) получаем

. (8.30)

2. В (8.26)

заменяем

, (8.31)

где учтено

,

,

.

В (8.31) разделяем вещественную и мнимую части

, (8.32)

, (8.33)

где учтено

,

.

При из (8.32) и (8.33) получаем разложение синуса и косинуса по функциям Бесселя

, (8.34)

. (8.35)

Рекуррентные соотношения

1. Производящую функцию (8.27)

дифференцируем по x

,

подставляем (8.27)

,

получаем

.

Сравниваем коэффициенты при

.

Обобщаем на случай произвольного порядка

. (8.36)

2. Производящую функцию (8.27)

дифференцируем по t

,

подставляем (8.27)

,

получаем

.

Сравниваем коэффициенты при

.

Для произвольного порядка

. (8.37)

3. Складываем и вычитаем (8.37) и (8.36)

,

находим

, (8.38)

. (8.39)

4. Умножаем (8.38) на и сворачиваем правую сторону

, (8.40)

где использовано

.

5. Симметризуем (8.40)

.

По индукции получаем

, (8.41)

6. Умножаем (8.39)

на и сворачиваем правую сторону

,

получаем

. (8.42)

7. Симметризуем (8.42)

.

По индукции получаем

, (8.43)

Частные соотношения

Из (8.39)

при находим

. (8.44)

Из (8.36)–(8.44)

,

,

,

,

,

при получаем соотношения между,и:

,

, (8.45)

,

,

,

,

. (8.46)

Условие ортонормированности

Множество функций

, ,,

образует непрерывный базис с условием ортонормированности

, . (8.48)

Доказательство:

Функции, входящие в (8.48):

, ,

являются решениями уравнения Ломмеля (8.3)

с параметрами

, ,

, .

Уравнение Ломмеля (8.2)

для иполучает вид

,

.

Умножаем первое равенство на xv, второе – на xu и вычитаем результаты

.

Преобразуем левую сторону

.

Интегрируем слагаемые по x от 0 до ∞

. (8.47)

Левая сторона на нижнем пределе дает нуль. На верхнем пределе используем (8.12а)

,

,

тогда

.

В результате

.

Учитываем (2.4)

,

,

тогда

,

Для нахождения интегрируем равенство пор от 0 до ∞, меняем порядок интегрирований, и используем условие нормировки (8.14)

.

Получаем

, ,

.

В результате доказано (8.48).

При не нулевой вклад в (8.48)

, ,

дает только . С учетомвыполняется

, . (8.49)

Доказательство:

Умножаем (8.49) на , где, и интегрируем поk от 0 до ∞

.

Меняем порядок интегрирований слева и учитываем справа

,

тогда

.

Внутренний интеграл согласно (8.48) равен

.

С учетом получаем тождество.