4.2. Момент импульса

Пусть дана материальная точка, имеющая импульср. Пусть её положение относительно точки О определяется радиусом-векторомr. Движение такой точки характеризуют моментом импульсаL.

Моментом импульса материальной точки относительно точки О называется векторная величина, равная векторному произведению радиуса-вектораr и вектора импульсаp:

L=[r,p].

Модуль момента импульса L=rpsin, где - угол между векторамиr и р. Направление вектора момента импульса определяется по правилу правого винта.

Размерность момента импульса [L]=кг^.м²/с.

М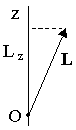омент импульса тела относительно точки равен векторной сумме моментов импульсов частиц тела относительно той же точки

L=L₁+L₂+…+L_N.

Проекция вектора момента импульса относительно точки О на ось z, проходящую через эту точку, называетсямоментом импульса относительно оси:

L_z=[r,p]_z.

Момент импульса относительно оси является скалярной величиной.

Момент импульса тела относительно оси z равен проекции момента им­пульса тела относительно точки О на осьz, проходящую через эту точку.

4.3. Связь момента силы и момента импульса

Момент импульса и момент силы связаны между собой. Найдём выражение, связывающее их.

Возьмём производную по времени от выражения, определяющего момент импульса:

Член равен нулю, так как угол между вектором скоростиdr/dt и вектором импульсар равен нулю.

Производная импульса по времени, имеющаяся во втором члене полу­ченного выражения, равна силе (второй закон Ньютона). Поэтому можем запи­сать полученное выражение в следующей форме:

.

Но [r,F] есть по определению момент силыF относительно той же точки О. Поэтому

т.е. скорость изменения момента импульса частицы равна моменту силы, действующему на эту частицу.

Проекция последнего уравнения на ось zвыражает связь момента им­пульса относительно осиzи момента силы относительно той же оси.

.

4.4. Основной закон динамики вращательного движения

Пусть твёрдое тело вращается относительно неподвижной оси z.

Выразим момент импульса твёрдого тела относительно оси вращения. Для этого представим твёрдое тело как совокупность элементарных масс. Момент импульса одной элементарной массы относительно осиz

Момент импульса всего тела равен сумме моментов импульсов всех эле­ментарных масс

Скорость vу разных элементарных масс различна, а угловая скорость одинакова.

Поскольку v=r,

Поскольку угловая скорость со одинакова для всех элементарных масс, её можно вынести за знак суммы

Введём обозначение . С учётом этого

L_z=J_z^..

Ранее мы получили, что момент импульса и момент силы связаны сле­дующим образом:

.

Заменив L_z наJ_zωи с учётом того, чтоJ_z с течением времени не изменяется, получаем

Учитывая, что производная угловой скорости по времени равна угловому ускорению , получаем

.

Полученное выражение - основной закон динамики вращательного движения, связывающий между собой меру внешнего воздействия - момент силы M_z с результатом внешнего воздействия - угловым ускорением.

Коэффициент J_z, стоящий в этом уравнении, зависит от массы тела и от то­го, как она распределена по объёму тела (это видно из определения величиныJ_z).

Чем меньше J_z, тем большее угловое ускорение получит тело при воздей­ствии момента силыM_z. Это говорит о том, что коэффициентJ_z. характеризует инертность вращающегося тела. ПоэтомуJ_z называют моментом инерции тела относительно осиz.

Знание величины момента инерции тела необходимо для описания враща­тельного движения. Поэтому обсудим более подробно, что такое момент инер­ции и как его вычислить.