7.2 Работа, совершаемая при изменении объёма системы

Вновь рассмотрим замкнутый сосуд с поршнем, внутри которого находится некоторое количество газа. Пусть сосуд находится внутри значительно большей макросистемы, также представляющей собой газ. Температура Тгаза во всех точках объёма сосуда одинакова. Площадь поршняS.

Газ, находящийся в сосуде, давит на поршень с силой F, под действием которой поршень переместится наdx. При этом газ совершит элементарную работуA=Fdx.

Сила, действующая на поршень, равна произведению давления газа на площадь поршня, поэтому элементарная работа равна A=PSdx.

Произведение площади поршня на совершённое им перемещение есть приращение объёма, занимаемого газом в сосуде dV. Тогда элементарная работа, совершённая газом при изменении объёма

A=PdV.

Работа, совершённая газом при конечном изменении объёма

.

Обратите внимание – работа, совершённая газом положительна, если газ увеличивает свой объём (в этом случае приращение объёма dVположительно). Если же объём газа уменьшается, то совершённая им работа отрицательна.

П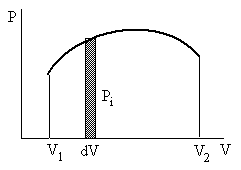роизведениеPdVс одной стороны равно элементарной работеA, а с другой - площади заштрихованного прямоугольника, показанного на рисунке. Поэтому работа, совершённая газом при изменении объёма, равна площади фигуры, образованной графикомP=f(V) на диаграммеPV.

Ещё одно важное замечание. Если газ, находящийся в сосуде увеличит свой объём на dV, то газ, окружающий сосуд, уменьшит свой объём на такую же величину. Следовательно, работа, совершённая газом в сосуде равна по величине и противоположна по знаку работе, совершённой внешними силами над системой:

A=-A.

7.3 ТЕРМОДИНАМИЧЕСКИЙ ПРОЦЕСС. ОБРАТИМЫЕ И НЕОБРАТИМЫЕ ПРОЦЕССЫ

Один и тот же газ может находиться в состояниях с разными значениями параметров состояния P,V,T. Переход газа (системы) из одного состояния в другое называютпроцессом.

Любой процесс связан с выходом системы из равновесного состояния. Например, если переместить поршень в сосуде с газом, то объём газа изменится. При этом изменится и давление газа, причём сразу после перемещения поршня давление газа в разных точках объёма станет разным – вблизи от поршня давление изменится сразу, а в удалённых точках объёма позже. Таким образом, равновесие системы нарушится. Причём равновесие нарушится тем сильнее, чем быстрее двигать поршень. Если же поршень двигать очень медленно, то нарушение равновесия будет незначительным. В пределе при бесконечно медленном перемещении поршня равновесие нарушаться не будет.

Это означает, что если процесс перехода системы из одного состояния в другое протекает бесконечно медленно, то каждое из промежуточных состояний будет равновесным. Такие процессы принято называть равновесными.

Если изменить направление равновесного процесса (например, заменив сжатие газа расширением), то система пройдёт в обратной последовательности через те же промежуточные равновесные состояния. Поэтому равновесные процессы называют обратимыми.

Реальные процессы всегда протекают за конечное время. Поэтому любой реальный процесс является неравновесным и поэтому необратимым.

В классической термодинамике рассматриваются только равновесные состояния и обратимые процессы. Реальные процессы рассматриваются в термодинамике неравновесных процессов, которая в данном курсе рассматриваться не будет.