6.8 Распределение больцмана

До сих пор мы считали, что на молекулы идеального газа не действуют никакие силы. Но на газ, находящийся над поверхностью Земли, действует сила тяжести. Возникает вопрос: как это сказывается на поведении молекул газа?

Рассмотрим вертикальный столб газа с площадью основания S. Пусть газ в столбе находится в состоянии равновесия.

Выделим в столбе горизонтальный слой газа толщиной dh. На него действуют сила тяжестиMg, приложенная к слою, сила давления со стороны вышележащих слоёв атмосферы и сила давления со стороны нижележащих слоёв атмосферы. Поскольку газ находится в равновесии, сумма этих сил равна нулю:

,

г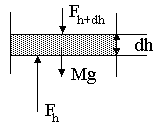деМ– масса газа в слое толщинойdh;g– ускорение свободного падения,F_h+dh– сила, действующая на слой со стороны вышележащих слоёв газа,F_h– сила, действующая на слой со стороны нижележащих слоёв газа.

Масса Мгаза в столбе площадьюSи высотойdhМ=Sdhnm_о, гдеn– концентрация молекул газа,m_о– масса одной молекулы газа.

Сила, действующая на слой со стороны нижних слоёв F_h=SР_h, со стороны вышележащих слоёвF_h+dh=SР_h+dh=S(Р_h+dР), гдеР_h– давление газа на высотеh,Р_h+dh– давление газа на высотеh+dh,dР– приращение давления при увеличении высоты наdh.

Таким образом,

Sdhnm_оg+S(Р_h+dР)-S^.p_h=0

и

dhnm_оg=-dР.

Поскольку давление Р=nkT, постольку приращение давленияdР=kTdn,

dhnm_оg=-kTdn,

.

Интеграл от этого выражения даёт , гдеn_о– концентрация идеального газа на высотеh=0. Потенцирование этого выражения даёт

.

Последнее выражение называется распределение Больцманав честь австрийского физика Людвига Больцмана, внёсшего заметный вклад в развитие молекулярно-кинетической теории. Оно показывает зависимость концентрации хаотически движущихся молекул от их потенциальной энергии. Из распределения Больцмана следует, что концентрация молекул больше там, где меньше их потенциальная энергия.

Больцман доказал, что распределение справедливо для газа, состоящего из одинаковых частиц, не только в поле сил земного тяготения, но и в потенциальных полях любых сил:

,

где U– потенциальная энергия частиц газа.

Ранее было показано, что Р=nkT. Следовательно

.

Полученное выражение называется барометрическая формула. Оно описывает зависимость давления газа от высоты в поле силы тяжести (в изотермической атмосфере). Из него видно, что по мере увеличения высоты давление газа уменьшается по экспоненциальному закону.

Увеличение температуры снижает скорость уменьшения давления с ростом высоты.

Скорость уменьшения давления газа с ростом высоты зависит и от массы молекулы идеального газа – чем больше масса молекулы, тем быстрее снижается давление газа.

Именно поэтому на больших высотах над Землёй кислорода становится мало – масса молекулы кислорода больше, чем масса молекул таких газов, как азот, водород и др.; концентрация лёгких газов с ростом высоты снижается медленнее и доля кислорода в единице объёма становится ниже.

6.9 Понятие о числе степеней свободы. Распределение энергии по степеням свободы

В механике используется понятие о числе степеней свободы, которое имеет следующее определение: число степеней свободы –это число независимых между собой возможных перемещений механической системы.

Поскольку поступательное движение любого тела можно представить как сумму трёх независимых перемещений вдоль осей x,y,z, постольку тело обладает тремя степенями свободы поступательного движения.

В разделе показано, что на каждое из независимых перемещений поступательного движения молекулы идеального газа вдоль осей координат x,y,zприходится средняя доля кинетической энергии, равная.

Но если на каждое из независимых перемещений приходится энергии поступательного движения, то и на каждую степень свободы поступательного движения приходится такая же доля энергии, равная.

Сформулированное в предыдущем абзаце утверждение в статистической механике называется законом равномерного распределения энергии по степеням свободы. Действие этого закона распространяется не только на поступательное движение молекул, но и на другие виды движения. Поэтому более корректная формулировка этого закона гласит:для макросистемы в состоянии равновесия на каждую степень свободы поступательного и вращательного движения приходится в среднем кинетическая энергия .

Частицу одноатомного идеального газа можно считать материальной точкой. Вращением такой частицы в молекулярной физике пренебрегают, так как радиус rтакой частицы пренебрежимо мал, соответственно мал и момент инерцииJ=mr²частицы относительно оси, проходящей через частицу. Поэтому и кинетическая энергия её вращенияпренебрежимо мала. Следовательно, полная механическая энергия частицы одноатомного идеального газа есть кинетическая энергия поступательного движения, равная. Это означает, чтоу молекулы одноатомного идеального газа три поступательных степени свободы.

Вращением молекул, состоящих из нескольких атомов пренебречь нельзя. Количество независимых перемещений во вращательном движении можно определить так же, как в поступательном движении. В разделе показано, что количество независимых перемещений в поступательном движении численно равно количеству проекций скорости поступательного движения на оси координат. Аналогично количество независимых перемещений во вращательном движении численно равно количеству проекций угловой скорости вращающегося тела на оси координат. В общем случае таких проекций три - _x,_y,_z. Поэтому и количество степеней свободы вращательного движения в общем случае равно трём.

Двухатомная молекула может двигаться поступательно и вращаться. Поэтому она должна иметь три поступательных степени свободы и три вращательных. Однако энергия вращения относительно оси, проходящей через атомы, пренебрежимо мала (J0,J²/20). Поэтому считают, что двухатомная молекула обладает не тремя, а двумя степенями свободы вращательного движения. Полноечисло степеней свободы двухатомной молекулы равно 5.

Поскольку двухатомная молекула имеет 5 степеней свободы, а на одну степень свободы в среднем приходится kT/2 кинетической энергии, средняя кинетическая энергия двухатомной молекулы равна.

Вращением молекул из трёх и более атомов пренебречь нельзя (если только атомы не расположены на одной прямой), поэтому такие молекулы имеют три поступательных и три вращательных степени свободы.

Средняя кинетическая энергия трёхатомной молекулы (и молекул, состоящих из большего количества атомов) равна .

В общем виде выражение для расчёта средней энергии любой молекулы имеет такой вид:

,

где i– полное число степеней свободы молекулы.