7.4 Изопроцессы

Если в ходе процесса один из параметров состояния остаётся постоянным, его называют изопроцессом. Масса газа в ходе изопроцесса не изменяется.

Рассмотрим существующие изопроцессы.

7.4.1 Изотермический процесс

Изотермическим называют процесс, в ходе которого температура газа постоянна.

Уравнение Менделеева-Клапейрона, записанное применительно к изотермическому процессу, принимает следующий вид:

PV=const,

где .

Графики зависимости параметров состояния для изотермического процесса изображе­ны на рисунке.

7.4.2 Изохорический процесс

Изохорическим называют процесс, идущий при постоянном объёме газа.

Уравнение Менделеева-Клапейрона, записанное применительно к изохорическому процессу, принимает следующий вид:

,

где .

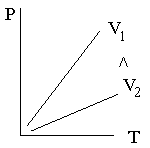
Графики зависимости параметров состояния для изо­хори­ческого процесса показаны на рисунке.

7.4.3 Изобарический процесс

Изобарическим называют процесс, идущий при постоянном давлении газа.

Уравнение Менделеева-Клапейрона, записанное применительно к изобарическому процессу, принимает следующий вид:

,

где .

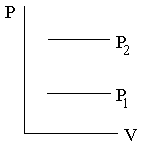
Графики зависимости параметров состояния для изобарического процесса приведены ниже:

7.5 ПРИМЕНЕНИЕ ПЕРВОГО НАЧАЛА ТЕРМОДИНАМИКИ К ИЗОПРОЦЕССАМ

Рассмотрим первое начало термодинамики применительно к системам, участвующим в изопроцессах. Перед этим отметим следующее.

При температуре Твнутренняя энергия газаUравна суммарной кинетической энергии всехNмолекул газа. Учитывая выражение для расчета средней кинетической энергии молекулы (см. , ), можем записать

.

Приращение внутренней энергии (это дифференциал от U) соответственно равно. Это означает, что внутренняя энергия может изменяться только при изменении температуры.

В разделе показано, что элементарная работа, совершаемая при изменении объёма системы равнаA=PdV. Это означает, что для того, чтобы система могла совершить работу, её объём должен изменяться.

7.5.1 Изотермический процесс

Изотермический процесс идёт при постоянной температуре. Следовательно, приращение температуры dT=0. Но тогда и приращение внутренней энергии равно нулю:dU=0.

Объём газа, участвующего в изотермическом процессе, может изменяться. Следовательно, газ может совершать работу, элементарная работа совершаемая газом A0, равно как и работа, совершаемая над системойA0.

Газ, участвующий в изотермическом процессе, может участвовать в теплообмене, поэтому и элементарное количество тепла, полученное системой не равно нулю: Q0.

Обобщая сказанное, получаем

0=Q+A

или

0=Q-A

и окончательно

Q=A.

Последнее выражение показывает вид первого начала при изотермическом процессе.

Прочесть его можно следующим образом: тепло, полученное системой при изотермическом процессе, идёт на совершение работы против внешних сил.

Обратите внимание на важную деталь: температура при изотермическом процессе постоянна. Значит, несмотря на то, что системе сообщается тепло, она не нагревается!

Найдём работу, совершаемую газом при изотермическом изменении объёма.

Как показано в разделе , работа при конечном изменении объёма равна .

Из уравнения Менделеева-Клапейрона следует, что давление газа равно , поэтому работа

.