Линейный гармонический осциллятор

Гармонический осциллятор колеблется по гармоническому закону. В области применимости квантовой механики он имеет эквидистантный спектр энергии с не равной нулю минимальной энергией. Поэтому состоянию n сопоставляют n квантов энергии. Электромагнитное поле в резонаторе и в свободном пространстве, упругие колебания узлов кристалла, колебания атомов в молекуле рассматриваются как гармонические осцилляторы.

Осциллятор в классической теории. Груз массой μ подвешен на пружине с коэффициентом жесткости κ. При смещении груза на расстояние x от положения равновесия потенциальная энергия и возвращающая упругая сила равны

,

.

Из второго закона Ньютона

получаем уравнение

,

где круговая частота

.

Решение

является колебанием с амплитудой и частотой. Тогда

. (3.23)

При максимальном отклонении

, .

Подставляем (3.23) и находим амплитуду колебаний

. (3.24)

Осциллятор в квантовой теории описывает уравнение Шредингера с потенциальной энергией (3.23)

. (3.26)

Переходим к безразмерному аргументу

, ,, (3.27)

.

Получаем уравнение

, (3.29)

где

. (3.30)

Согласно курсу «Методы мат. физики» при целочисленном решение выражается через полином Эрмита

.

При s не целом , нормировочный интегралне существует, и такое решение не физическое. Поэтому полагаем

Из теории полиномов Эрмита получаем условие ортонормированности

.

При

выполняется ортонормированность

для состояний

. (3.32)

Учитывая ,, , из (3.32) находим

,

. (3.32а)

Ортонормированность и рекуррентные соотношения. Из результатов прошлого семестра:

, (3.33)

, (3.34)

. (3.35)

Матричные элементы координаты и импульса являются измеримыми величинами

,

.

Используя (3.33–35), находим

, ,

, . (3.37)

Для средних значений и флуктуаций в состоянии n получаем

,

,

,

,

,

. (3.38)

Энергия состояния. Из

, ,

получаем

. (3.39)

Спектр эквидистантный, расстояние между соседними уровнями

.

Номер квантового состояния n равен числу квантов энергии , связанных с осциллятором. Переход к соседнему состоянию добавляет или удаляет квант энергии. Энергия основного состояния

.

Отсутствие состояния покоя у пространственно ограниченной системы следует из соотношения неопределенностей Гейзенберга.

Квазиклассическое квантование вкб

Точное аналитическое решение уравнения Шредингера возможно лишь для ограниченного числа функций потенциальной энергии. Для других случаев используются приближенные аналитические и численные методы. Приближенным аналитическим решением является квазиклассическое квантование. Метод разработали Грегор Вентцель, Хендрик Крамерс и Леон Бриллюэн в 1926 г., отсюда название ВКБ.

Метод ВКБ применим, если длина волны де Бройля частицы гораздо меньше расстояния существенного изменения потенциальной энергии. Малая длина волны означает близость к классическому поведению. В отличие от ранее рассмотренной полуклассической квантовой механики, квантование ВКБ дает более точные результаты. Метод применим для частицы, движущейся с большим импульсом в области с плавно изменяющимся потенциалом. Метод не применим к скачкообразным потенциалам и к резонансным явлениям.

Уравнение Шредингера (3.1) для частицы c энергией Е в поле с потенциальной энергией записываем в виде

, (3.51)

где

– импульс в точке x. В точках поворота классического движения ичастица останавливается

, ,.

Между точками поворота кинетическая энергия положительная, импульс вещественный, решение ищем в виде волны

, (3.52)

где – фазовая комплексная функция;– амплитуда. Подставляем (3.52) в (3.51), учитываем

,

,

получаем уравнение для фазовой функции

. (3.53)

Уравнение нелинейное, решаем его методом последовательных приближений.

Первое приближение. Изменение фазы считаем медленным

и не учитываем вторую производную в (3.53). Уравнение упрощается

. (3.54)

Интегрируем

,

находим

. (3.55)

Фаза волновой функции определяется интегралом от импульса по пути между точкой поворота и текущим положением частицы. Результат совпадает с условием квантования Бора–Зоммерфельда полуклассической квантовой теории.

Условие применимости решения (3.55). Из (3.54) получаем модуль отброшенного слагаемого

. (3.55а)

Для его анализа используем

, ,

, . (3.55б)

Медленность изменения фазы

с учетом (3.55а) означает ограничение на импульс

.

Тогда

,

– длина волны медленно меняется от точки к точке. Из (3.55б) иполучаем

(3.56)

– поле изменяется медленно. Поэтому при разложении в ряд Тейлора около точки поворотаx₁ ограничиваемся первыми двумя слагаемыми

,

, (3.56а)

где – расстояние от точки поворота до области, где применимо (3.56). Используя (3.56а) и (3.56), находим

. (3.56б)

В неравенстве

приводим подобные

. (3.56в)

С учетом

из (3.56в) находим

(3.57)

– длина волны гораздо меньше расстояния до точки поворота.

Подставляем (3.56в) в первый элемент строки (3.56б), тогда

.

Приводим подобные и получаем расстояние до точки поворота, где применимо решение ВКБ:

, (3.57а)

здесь

.

Квазиклассическое приближение применимо вдали от точки поворота, когда длина волны де Бройля гораздо меньше расстояния, на котором существенно изменяется потенциальная энергия. Это соответствует большому импульсу и его малому изменению на протяжении указанного расстояния. Решение ВКБ неприменимо вблизи точки поворота, где

, ,.

Второе приближение. В точное уравнение (3.53)

подставляем (3.55а) и получаем

,

тогда

. (3.57б)

Учитываем ранее полученное неравенство

в виде

,

Следовательно, второе слагаемое в круглой скобке (3.57б) мало. Разлагаем выражение в ряд по степеням малого параметра и оставляем первые два слагаемые согласно

,,

получаем

.

Интегрируем

, (3.57в)

где использовано

.

Результат

подставляем в (3.52)

,

получаем общее решение

. (3.58)

По сравнению с квантованием Бора–Зоммерфельда в (3.58) присутствует множитель . В плотности вероятности

множитель связан с тем, что с увеличением скорости уменьшается время пребывания частицы в единичном интервале около рассматриваемой точки.

Вне классической области при и получаем и мнимый импульс. В решении ВКБ (3.58) оставляем функции, убывающие при удалении от точек поворота:

, (3.60)

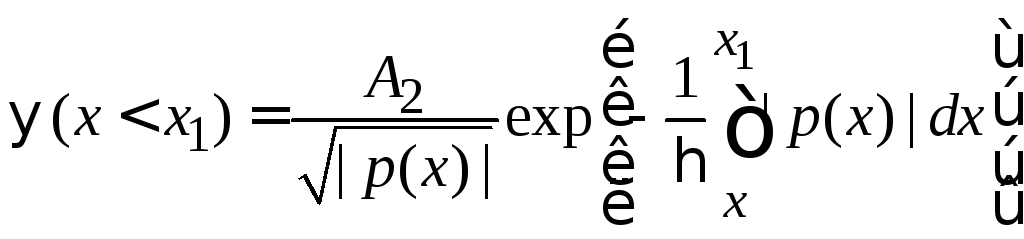. (3.61)