ДВУХМЕРНЫЕ И ТРЕХМЕРНЫЕ СИСТЕМЫ

Двухмерные и трехмерные системы могут совершать не только поступательное, но и вращательное движение. Электрон, связанный кулоновской силой с положительным зарядом, вращается вокруг общего центра масс. Свободный электрон также может иметь неравный нулю орбитальный угловой момент. При этом его волновая поверхность вращается вокруг вектора скорости, образуя вихрь. Максимум вероятности обнаружения электрона перемещается по винтовой линии, на ее оси вероятность обнаружения электрона равна нулю благодаря центробежной силе. При отсутствии осевой скорости вероятность распределена по кольцу равномерно, и центр масс неподвижен. В квазиклассическом описании вихрь является когерентной суперпозицией прямолинейных траекторий, смещенных от оси вихря.

Вращение описывается операторами момента импульса и их собственными функциями.

Момент импульса

В классической механике момент импульса

имеет декартовы проекции и модуль

,

,

,

. (4.1)

Выполняется симметрия при циклической перестановке

.

Операторы момента импульса

Декартовые координаты. По правилу соответствия между классическими и квантовыми соотношениями величины в (4.1) заменяем операторами и получаем оператор момента импульса

, (4.2)

где операторы проекций

;

;

, (4.3)

оператор квадрата момента импульса

. (4.4)

Перестановочные соотношения следуют из (4.3)

,

,

,

. (4.5а)

Следовательно, и измеримы одновременно с неограниченной точностью, наборы их собственных функций совпадают. Операторы эрмитовые

, . (4.5б)

Соотношения (4.5а) и (4.5б) доказываются на практических занятиях.

Сферические координаты связаны с декартовыми координатами

; ; ,

,

,

,

Операторы в сферических координатах рассматривались в курсе «Методы математической физики»

, (4.6)

. (4.7)

Оператор Лапласа

, (4.8)

где радиальная часть оператора Лапласа

, (4.9)

радиальный импульс

, (4.9а)

,

. (4.9б)

Соотношения (4.9) – (4.9б) доказываются на практических занятиях.

Повышающий и понижающий операторы

(4.10)

удовлетворяют соотношениям

,

, (4.11)

, (4.12)

. (4.13)

Соотношения (4.11) – (4.13) доказываются на практических занятиях.

Сферическая функция

Функция является собственной функцией и

, (4.14)

, (4.15)

где – магнитное квантовое число, определяет проекцию L на ось z

;

– орбитальное квантовое число, определяет модуль L

. (4.16)

Состояния обозначаются s, p, d, f

(от англ. sharp – резкий, principal – главный, diffuse – расплывчатый, fundamental – фундаментальный).

Число проекций L на ось z равно числу возможных значений m

.

Направление L квантуется

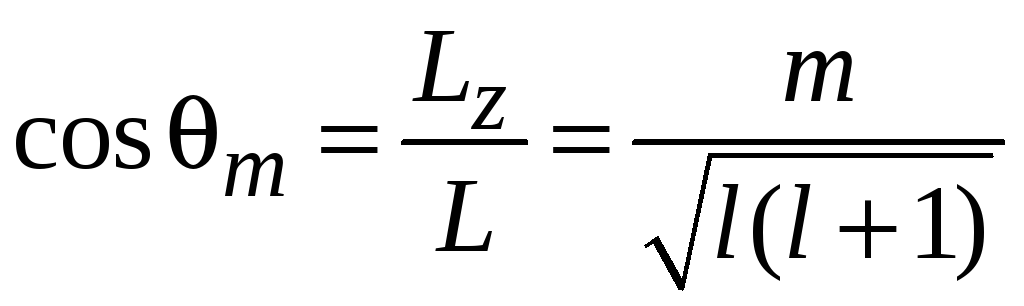. (4.17)

Пространственное квантование при l = 3

Вектор L не может быть направлен вдоль оси z, поскольку максимальная проекция меньше модуля , тогда согласно (4.17) и . Физическая причина в том, что определенность приводит к неопределенностям некоммутирующих с ним и , которые дают вклад в , поэтому .

Из (4.12)

и (4.15)

получаем

.

Следовательно, операторы переводят состояние с собственным значением m в состояния с собственными значениями , т. е. повышает у состояния число m на единицу, а понижает на единицу.

Выполняется

, (4.18)

Выражение для сферической функции. Подстановка (4.6)

в (4.15)

дает уравнение

. (4.19а)

Решение должно удовлетворять условию периодичности

. (4.19б)

Из (4.19а) и (4.19.б) получаем

, (4.21)

Условие периодичности (4.19б) привело к квантованию числа m. Ограничения сверху на m пока нет. На основании

выполняется условие ортонормированности

. (4.22)

Выражение (4.7)

подставляем в (4.14)

,

получаем дифференциальное уравнение

.

Переменные разделяются, тогда ищем решение в виде

.

Подстановка решения в уравнение и использование (4.21) приводит к уравнению для

. (4.20)

Уравнение совпадает с уравнением для присоединенных функций Лежандра , тогда ,

.

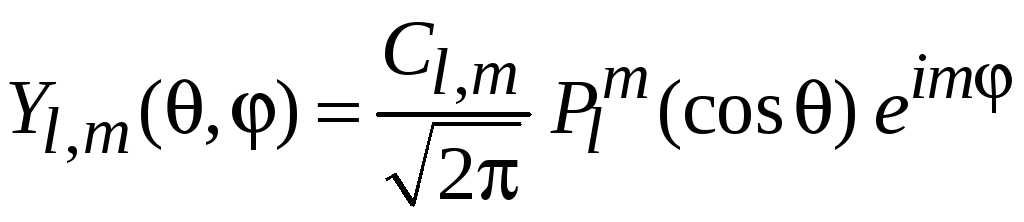Постоянный множитель определяется из условия нормировки

, .

В результате

. (4.23)

Выполняются

, (4.24)

,

,

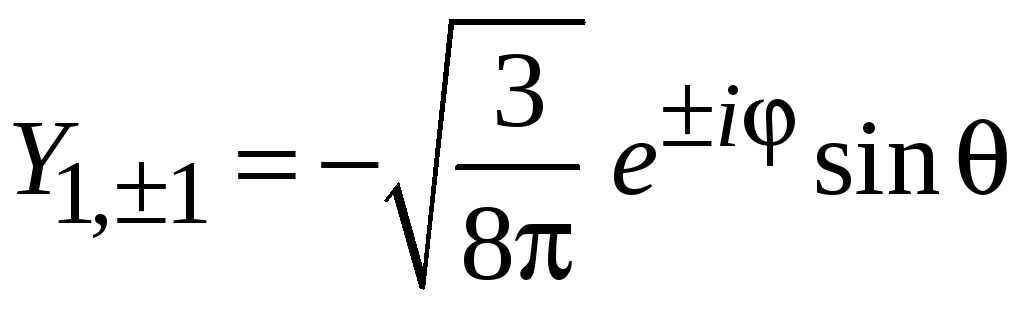. (4.25)

Условие ортонормированности

. (4.26)

Инверсия координат соответствует замене

, ,

тогда

. (4.27)

Четность состояния, описываемого сферической функцией, совпадает с четностью орбитального числа l.

7