9. Включение резистора на заряженную ёмкость

Рассчитать переходный процесс для тока i(t) протекающий при включении резистора R₂ в цепь (рис. 1), при заданных параметрах:

E =15 В, R=100 Ом, R₂ = 200 Ом, L = 0.3 Гн, и C =5 мкФ.

R₁

E

Кл

C

i

R₂

L

Рис. 1

Переходный процесс, протекающий в цепи (рис. 1) описывается системой дифференциальных уравнений второго порядка, составленной по законам Кирхгофа для режима после коммутации:

E= i_L R₁ + i R₂ + u_L

0 = i R₂ − u_C (1)

i_L − i − i_C = 0

где i_C = C и u_L = L_; (2)

а б

Рис. 2

Решение системы дифференциальных уравнений (1) и (2) проведём классическим методом.

1. Записываем общее решение искомого тока:

i(t) = i _ПР(t)+ i _СВ(t). (3)

2. Определим принуждённую составляющие i _ПР(t).

Принуждённая составляющая находится по схеме замещения, построенная для устанавливающегося режима постоянного тока после коммутации при t=∞ рис. 2а,

Составим уравнение по второму закону Кирхгофа;

E= i_LПР R₁ + i_ПР R₂ + u_LПР

0 = i_ПР R₂ − u_CПР (5)

i_LПР − i_ПР − i_CПР = 0

учтём, что i_CПР = 0 и u_{L ПР}= 0, подставим их в (1) и получим:

i_ПР = i_LПР = E/( R + R₂ ) = 0.5 А,. (6)

3. Находим свободную составляющую i _СВ(t).

3.1. Составим характеристическое уравнение.

_{По схеме замещения рис. 2б составим главный определителя системы уравнений методом контурных токов и приравняем его нулю}

ΔKT(p)=	R1+R2+pL	R2	= (R1+R2+pL)(R2+) – R22 = 0
	R2	R2+

или p² + р += 0

p² + B р + Q = 0 (7)

B = =1333 иQ = = 2 10⁶ (8)

Найдём корни уравнения (7):

p_1,2 = −  = −  _, (9)

где D = = − 1.556 10⁶ дискриминант уравнения (7). (10)

p₁₂ = − δ ± ω_CB = − 666.7. ± j 1247;

δ = 666.7 с^-1 − коэффициент затухания; (11)

ω_CB = 1247 рад/с − частота собственных колебаний (12)

При D < 0 характеристическое уравнение имеет два комплексно сопряжённых корня – p₁₂ = − δ ± ω_CB, процесс колебательный и свободные составляющие имеют вид:

i _СВ(t) = Ae^-δt siu(ω_СВ t+Ψ); (13)

3.2. Определяем постоянные интегрирования.

3.2.1. Постоянные интегрирования определяются из начальных условий для искомого тока и его производной. Так, общее решение для тока i при колебательном режиме при D < 0 получаем из системы из двух уравнений:

i (t)= i _ПР(t) + A e^-δt siu(ω_СВ t + Ψ);

и для производной

i^′ (t) = i^′ _ПР(t) + A δ e^-δt siu(ω_СВ t + Ψ) + A ω_СВ e^-δt cos(ω_СВ t + Ψ)

_{Запишем эту систему для t=0+}

i (0)= i _ПР(0) + A siu(Ψ);

i^′ (0)= i^′ _ПР(0) + A δ siu(Ψ) + A ω_СВ cos(Ψ) (14)

3.2.2. Определяем независимые начальные значения i_L(0_–) = i_L(0₊) и u_C(0_–) = u_C(0₊).

До коммутации резистор R₂ отключен, в цепи установившийся режим постоянного тока рис. 3.

R₁

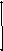
Кл

E

C

Токи в цепи равны нулю, а напряжение на ёмкости определим по второму закону Кирхгофа:

i_С(0_–) = i(0_–) = i_L(0_–) = i_L(0₊) = 0 и u_C(0_–) = u_C(0₊) = E = 150 B. (15)

3.2.3. Определяем зависимые начальные значения i (0) и i^′(0) из системы уравнений составленных по законам Кирхгофа, для исследуемой цепи сразу после коммутации (1):

E= i_L R₁ + i R₂ + u_L

0 = i R₂ − u_C (16)

i_L − i − i_C = 0

Систему уравнений запишем в момент времени t=0₊, и подставим в неё законы коммутации:

E= i_L(0₊) R₁ + i(0₊) R₂ + u_L(0₊); 150= i(0₊) 200 + u_L(0₊)

0 = i(0₊) R₂ − u_C(0₊); 0 = i(0₊) 200 − 150 (17)

i_L(0₊) −i (0₊) − i_C (0₊); 0=− i (0₊) − i_C (0₊)

Из системы определяем:

i(0₊) = −i_C (0₊) = E / R₂ = 0.75 А; u_L(0₊) = 0; (18)

u′_C (0₊) = = −= −= −7.5 10⁴ В/с. (19)

i′_L (0₊) = = 0A/с. (20)

Продифференцируем систему (16) и запишем её в момент времени t=0₊ ,

0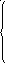= i′_L(0₊) R₁ + i′(0₊) R₂ + u′_L(0₊) i′(0₊) R₂ + u′_L(0₊) = 0

0 = i′(0₊) R₂ − u′_C(0₊) i′(0₊) R₂ + = 0 (21)

i′_L(0₊) − i′(0₊) − i′_C(0₊) = 0 −i′(0₊) − i′_C(0₊) = 0

i′(0₊) = − i′_C(0₊) = −= − 750A/с. (22)

3.3.4. Подставив начальные значения в систему уравнений (14) с учётом (18) и (22) получим постоянные интегрирования A и Ψ

= + A siu(Ψ);

− = 0 + A δ siu(Ψ) + A ω_СВ cos(Ψ) (23)

Решая (23) получим:

i_CB(0₊) =− = A siu(Ψ);

i′_CB(0₊) = − = A δ siu(Ψ) + A ω_СВ cos(Ψ); (24)

окончательно получим постоянные интегрирования A и Ψ:

Ψ = arctg=−28.1° и A = – =−0.53 А. (25)

Подставив начальные значения (19), (25) в систему уравнений (18) с учётом (6)

4. Записываем полное решение для искомой величины x (t).

В нашем примере напряжения u_C (t) и строим график процесса (рис. 10).

i (t)= 0.5 + −0.53 e^-δt siu( 1247 t −28.1°); (26)

Рис. 4

На рис. 3 изображены графики переходного процесса для тока , где кривая соответствует колебательному переходному процессу.

15