4. Классический метод расчёта переходных процессов

Решение дифференциального уравнения (15) классическим методом - x(t) представляется суммой двух составляющих [7]

x(t)=x_ПР(t)+x_СВ(t), (20)

где

x(t) - решение искомых токов или напряжений, например, u_C(t), u_L(t), i(t) и др.,

x_ПР(t) - принуждённая составляющая, которая является частным решением неоднородного обыкновенного дифференциального уравнения (15) и определяет установившееся значение тока или напряжения после коммутации.

x_СВ(t) - свободная составляющая которая является общим решением однородного обыкновенного дифференциального уравнения (15) в котором правая часть принимается равной нулю.

Общее решение x_СВ(t) представляется в виде суммы экспонент:

, (21)

где ,…, - корни характеристического уравнения, и ,…, - постоянные интегрирования.

Для получения характеристического уравнения в (15) заменяется производные на p, интегралы на -, и правая часть уравнения полагается равной нулю:

. (22)

Постоянные интегрирования определяются из системы уравнений составленной для начальных значений искомой функции – x(0) и её производных - в момент коммутации . Для цепи второго порядка n=2 такая система примет вид

(23)

Характер свободной составляющей переходного процесса для всех токов и напряжений одной и той же цепи одинаков и зависит только от параметров R, L и C цепи и определяется корнями характеристического уравнения ….

Свободная составляющая связывает начальное значение функции x(0) с установившимся после коммутационным значением и обеспечивает непрерывное приближение тока или напряжения к её установившемуся значению. Теоретически, переходный процесс длится бесконечно большое время, но практически он заканчивается за некоторое конечное время.

5. Порядок расчёта переходных процессов классическим методом

Рассмотрим пример решения дифференциального уравнения (18) с начальными значениями (19) классическим методом.

1. Запишем общее решение искомого тока или напряжения:

x(t)= x _ПР(t)+ x_СВ(t).

В нашем примере это напряжения на ёмкости (рис. 2)

u_C(t)= u_{C ПР}(t)+ u_{C СВ}(t). (24)

2. Определим принуждённую составляющую искомой величины x _ПР(t) по схеме замещения, для установившимся режима после коммутации при t=∞

Принуждённую составляющую u_CПР(t) Определим по схеме замещения рис. 6, которая является установившимся значением напряжения на ёмкости после коммутации при t=∞

Рис. 6

Уравнение по второму закону Кирхгофа;

Е₂ = u_{R ПР} + u_{L ПР} + u_{C ПР} учтём, что u_{R ПР}=0 и u_{L ПР}=0, откуда u_{C ПР} =Е₂ (25)

3. Находим свободную составляющую x_СВ(t).

В примере это u_{C СВ}(t).

3.1. Составим характеристическое уравнение.

Для чего в неоднородном уравнении (18) приравняем правую часть нулю и получим однородное уравнение:

+ + u_C = 0 (26)

В уравнении (26) производные заменим умножением на комплексное число p и в результате получим характеристическое уравнение второго порядка:

p² + р +q = 0 (27)

или p² + b р + q = 0

найдём корни уравнения (27) p_1,2 = −  = − (28)

В зависимости от знака подкоренного выражения D решение для свободной составляющей напряжения на емкости имеет три различных выражения:

1. D > 0, два действительных отрицательных корня – p₁ и p₂, процесс апериодический, кривая 1 рис. 7.

u_{C СВ}(t) = A₁e^p1t + A₂e^p2t; (29)

2. D < 0, два комплексно сопряженных корня - p₁₂= – δ ± j ω_СВ, процесс колебательный, кривая 2 рис. 7.

u_{C СВ}(t) = Ae^-δt siu(ω_СВ t+Ψ); (30)

3. D = 0, два равных действительных отрицательных корня -, процесс критический, кривая 3 рис. 7.

u_{C СВ}(t) = (A₁ + A₂t) e^pt. (31)

В (29)…(31) A, A₁, A₂ и - постоянные интегрирования, δ- коэффициент затухания колебательного процесса, ω_СВ - частота собственных затухающих или свободных колебаний цепи.

B

u_{C СВ}

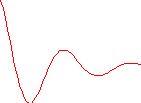
u_{C СВ}(0)

1

2

0

t

C

3

Рис. 7

Примечание.

1. Характеристическое уравнение может быть получено непосредственно по специальной схеме замещения, которая составляется для после коммутационной цепи путём замены индуктивности L на сопротивление – pL, ёмкости C заменяется на – _{, вместо источников остаются их внутренние сопротивления (для идеального источника ЭДС это сопротивление равное нулю, а для идеального источника тока - бесконечно большое сопротивление).}

_{Так для примера рис. 2 схема замещения для составления характеристического уравнения при ведена на рис. 8.}

Рис. 8

_{По схеме рис. 8 можно получить характеристическое уравнение несколькими способами:}

• _{Определение входного сопротивления цепи относительно разрыва в любой ветви цепи и приравнять его нулю:}

Z_BX = R + p L + = 0, илиp² + р +q = 0

• _{Составление главного определителя системы уравнений метода контурных токов, законами Кирхгофа или узловых потенциалов и приравнять его нулю. Например, метод контурных токов:}

Δ_KT = R + p L + = 0

Рассмотрим второй пример рис.9а.

≈

а б

Рис.9.

Рис.9а схема до коммутации.

Рис.9б схема после коммутации для составления характеристического уравнения.

• _{Определение входного сопротивления цепи относительно разрыва, например, в ветви с ёмкостью и затем приравнивая его нулю:}

+ = 0, илиp² + р += 0

• _{Составление главного определителя системы уравнений методами:}

_{- контурных токов}

ΔKT =	R+pL	–R	= (R+pL)( R+) + R2 = 0
	–R	R+

или p² + р += 0

_{-законами Кирхгофа}

ΔЗК =	1	–1	–1	= R+ R pL + = 0
	pL	R	0
	0	–R	+

и

или p² + р += 0

_{-узловых потенциалов}

Δ_УП = ++pС = 0 или p² + р += 0

2. Если в цепи после коммутации остаётся один реактивный элемент, то дифференциальное уравнение будет иметь первый порядок, а характеристическое уравнение один корень:

Ap + B = 0 и p = – B/A,

и общее решение для свободной составляющей:

x_{C СВ}(t) = A₁e^pt

3.2. Определяем постоянные интегрирования.

3.2.1. Постоянные интегрирования определяются из начальных условий для искомого тока или напряжения. Так, общее решение для напряжения на емкости при апериодическом режиме D > 0 получаем систему из двух уравнений:

u_C (t)= u_{C ПР}(t) + A₁e^p1t + A₂e^p2t ;

и для производной

u^′_C (t)= u^′_{C ПР}(t) + A₁ p₁e^p1t + A₂ p₂e^p2t

_{Запишем эту систему для t=0+}

u_C (0)= u_{C ПР}(0) + A₁ + A₂ ;

u^′_C (0)= u^′_{C ПР}(0) + A₁ p₁ + A₂ p₂ . (35)

3.2.2. Определяем независимые начальные значения i_L(0_–) = i_L(0₊) и u_C(0_–) = u_C(0₊), см. (5) –(6):

i(0_–) = i_L(0_–) = i_L(0₊)=0 и u_C(0_–) = u_C(0₊) = E₁. (36)

3.2.3. Определяем зависимые начальные значения u^′_C (0) по законам Кирхгофа, составленным для исследуемой цепи сразу после коммутации в момент времени t=0₊ , в которые подставляются законы коммутации, см. (7) –(14):

u′_C (0₊) = = 0. (37)

3.3.4. Подставив начальные значения в систему уравнений (35) с учётом (36) и (37) получим постоянные интегрирования

E₁ = E₂ + A₁ + A₂ ;

0 = 0 + A₁ p₁ + A₂ p₂ (38)

Решая (38) получим:

A₁ = – p₁ и A₂ = p₂

4. Записываем полное решение для искомой величины x (t).

В нашем примере напряжения u_C (t) и строим график процесса (рис. 10).

u_C (t)= E₂ + A₁e^p1t + A₂e^p2t . (39)

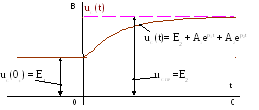
Рис. 10

11