Эл-ка / 05 Лекции АВТ / UE_mod_5 / l 512
.docL. 512. «Электротехника» Аксютин В.А.
Обобщённые законы коммутации
При проведении исследования переходных процессов в электрических цепях встречаются случаи, когда применить напрямую рассмотренные ранее закона коммутации невозможною. Примеры таких цепей приведены на рис. 1. В таких цепях протекают переходные процессы при мгновенном изменении реактивных параметров участков цепи (при “некорректных” коммутациях). В таких случаях переходный процесс можно разбить на два этапа. Первый этап связан с перераспределением энергии между реактивными элементами, участвующими в процессе, например, индуктивностями L1 и L2, схема рис. 11а, и ёмкостями, C1 и C2 схема рис. 1б. Данный процесс является скоротечным, вызывает большие напряжения между контактами ключа, и приводит к появлению электрической искры или дуги. Кроме того, ранее не учитывались сопротивления проводов и контактов соединений, наличие распределённой ёмкости между витками катушки и т. п. Разность суммарных энергий W(0−) − W(0+) в реактивных элементах расходуется в неучтённых активных сопротивлениях цепи и излучении при весьма высоких частотах. Второй этап связан с дальнейшим перераспределением энергии между источником и реактивными элементами во всей цепи. На этом этапе и определяется основное время переходного процесса.
Для приближённого учёта этого явления вводятся обобщённые законы коммутации.
а б
Рис. 1
Рассмотрим цепь рис. 1а.
До коммутации
i1(0−)=
,
i2(0−)
= 0. После коммутации i1(0+)
= i2(0+).
i1(0+)
i1(0−)
и i2(0+)
i2(0−)
- нарушение первого закона коммутации
в ранее принятом виде.
Токи в катушках изменятся скачком, что возможно только при бесконечно больших напряжениях на катушках. Суммарное напряжение u − конечно. Следовательно,
uL1(0)
= L1
= − uL2(0)
= − L2
.
Интегрируя это равенство в пределах от t = 0− до t = 0+ , находим
L1
= − L2
или
L1
= − L2
.
То есть L1 (i1(0+) − i1(0−)) = − L2 (i2(0+) − i2(0−))
или L1 i1 = − L2 i2 или 1 + 2 = 0.
Первый обобщенный закон коммутации.
Потокосцепление любого замкнутого контура в момент коммутации (t = 0+) равно алгебраической сумме потокосцеплений всех входящих в него катушек, которые последние имели непосредственно до коммутации (t = 0−). Некоторые из этих катушек перед коммутацией могли и не составлять одного замкнутого контура, а образовали его лишь после коммутации.
Этот закон можно использовать и для цепей с взаимной индуктивностью.
В данной задаче:
(0−) = L1 i1(0−) + L2 i2(0−) = L1 i1(0−); (0+) = (L1 + L2) i(0+).
Но
(0−)
= (0+).
Отсюда
i1(0+)
= i2(0+)
= i(0+)
=
i1(0−).
Энергия магнитного
поля до коммутации: WМ(0−)
=
.
После коммутации:
WМ(0+)
=
=
=
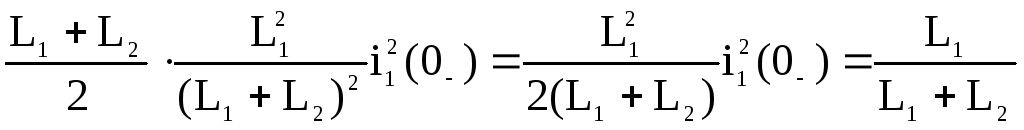WМ(0−)
< WМ(0-).
Разность этих энергий расходуется на необратимые процессы во время коммутации, хотя длительность коммутации бесконечно малая. Это возможно, так как на участках цепи развиваются бесконечно большие мощности.
Аналогично в схеме рис. 1б напряжения uC1 и uC2 изменятся скачком ввиду большого тока между конденсаторами, то есть
С1
= − С2
; С1
= − С2
.
С1 uC1 = − C2 uC2 или q1 + q2 = 0.
Второй обобщенный закон коммутации.
Сумма зарядов на всех параллельно включенных конденсаторах перед коммутацией (t = 0−-) равна сумме зарядов на этих же конденсаторах непосредственно после коммутации (t = 0+).
Легко убедиться, что WЭ(0+) < WЭ(0−).