Сетевой график комплекса работ. Временной сетевой график.

Предположим, что нам дана упорядоченная структурная таблица комплекса работ (таблица 6.4). Связи между работами, входящие в этот комплекс, можно изобразить графически, в виде так называемого сетевого графика (или графа).

Э

Таблица 6.4

Работа	Опирается на работы
a1	-
a2	-
a3	-
a4	a1, a2
a5	a2, a3
a6	a4
a7	a5, a6
a8	a3, a5, a6
a9	a7
a10	a5, a8

тот график можно строить по-разному. Чаще всего изображают работы, входящие в комплекс, стрелками, а события состоящие в выполнении каких-то работ и возможности начать новые работы – кружками или «узлами». Изобразим в виде сетевого графика структуру таблицы 6.4 (рис.6.1). Узлы обозначим А₀, А₁, А₂,…, работы а₁, а₂,…. Исходный узел всего комплекса работ обозначим А₀ и будем понимать под ним начало работ или принятие решения о начале работ. Из этого узла исходят стрелки а₁, а₂, а₃, изображающие соответствующие работы и идущие соответственно в узлы А₁, А₂, А₃. Совместное выполнение работ а₁, а₂ будем изображать дополнительным узлом А_1,2, в который ведут пунктирные стрелки, не изображающие никаких работ, а означающие только логическую связь.

Из узла А_1,2 исходит стрелка а₄, изображающая работу а₄, опирающаяся на работы а₁, а₂; в конце стрелки стоит узел А₄, означающий выполнение работы а₄, и т. д. Завершающий узел А означает конец всего комплекса работ. На графе опущены связи, логически вытекающие из других; например, работа а₈ в табл. 6.4 опирается на работы а₃, а₅, а₆; на графе она показана опирающейся только на работы а₅, а₆, т. к. сама работа а₅ опирается на а₃ и без её выполнения не может быть начата.

A₄

a₄

a₆

A₁

A_{1, 2}

A₆

a₁

A₈

A₁₀

a₁₀

a₈

A₀

A₂

a₂

A_{5, 6}

A

a₃

a₇

A₇

A₉

a₉

A₃

A_{2, 3}

a₅

A₅

Р

a₁

ис. 6.1

Как уже было сказано, существуют разные формы сетевых графиков, например, узлами обозначаются работы, а стрелками – логические связи между ними (структурную таблицу 6.4 можно изобразить графически по этому способу рисунком 6.2).

a₁

a₄

a₆

a₈

a₁₀

a₂

a₃

a₅

a₇

A₉

Рис. 6.2.

Таблица 6.5

№ n/n	Работа аi	Опирается на работы	Время ti
1	a1	-	10
2	a2	-	5
3	a3	-	15
4	a4	a1, a2	18
5	a5	a2, a3	19
6	a6	a4	18
7	a7	a5, a6	8
8	a8	a5, a6	25
9	a9	a7	30
10	a10	a8	8

Каждый из способов построения сетевого графика имеет свои преимущества и свои недостатки. Преимуществом второго способа является то, что в него легко внести новые, ранее не указанные связи, которые обнаруживаются в ходе выполнения работ. Преимуществом первого способа является то, что он может быть сравнительно просто приспособлен к учету времени выполнения отдельных работ и комплекса в целом. Поэтому будем пользоваться первым способом.

Пусть задана структурная таблица комплекса работ, в которой поставлены времена выполнения каждой работы: t₁, t₂,…. Эти значения времен выполнения отдельных работ будем предполагать не случайными, а известными заранее. Получится таблица 6.5, в которой структурные связи – те же, что в табл. 6.4 и на графиках рис. 6.1, 6.2 (устранены только лишние связи), а в правом столбце указаны времена выполнения отдельных работ, выраженные в любых единицах времени (часы, недели, месяцы). Такую таблицу будем называть структурно- временной.

Временную структуру комплекса работ, вместе с логической структурой, можно изобразить на одном и том же графике, который мы будем называть временным сетевым графиком. Будем его строить следующим образом. График ориентируется вдоль оси времени 0t, на который в каком-то масштабе откладываются времена выполнения работ. Как и на графике рис. 6.1, стрелками изображаются работы, но длина каждой стрелки не произвольна, а такова, что её проекция на ось абсцисс 0t равна времени выполнения данной работы. Логические связи между работами опять обозначены пунктирными стрелками, не означающими никакой реальной работы («фиктивные» работы).

A₈

A₂

a₈

a₁₀

a₅

A₃

A₅

A₆

a₂

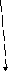
A₁₀

a₃

A₀

t

10

20

30

40

50

70

60

80

a₇

a₆

a₁

A₇

A₄

a₉

A₁

a₄

A₉

Рис .6.3

При построении временного сетевого графика расположение узлов по вертикали (по оси ординат) берется произвольным, абсцисса же каждого узла равна времени окончания соответствующей работы. Длина каждой стрелки считается от центра до центра кружка. Проследим, как строится временной сетевой график на рисунке 6.3. Начинаем его с узла А₀, помещенного в начале координат.

Из этого узла исходит три стрелки: a₁, a₂ и a₃, проекции которых на ось 0t равны времени выполнения соответствующих работ: t₁ = 10, t₂ = 5 и t₃ = 15. Работа a₄ опирается на работы a₁ и a₂; из них работа a₂ кончается в момент t₂ = 5, а работа a₁ – в момент t₁ = 10; значит, работа a₄ может начаться не раньше, чем в момент t₁ = 10, когда окончена a₁. Начнём стрелку а₄ из узла А₁, а узел А₂ соединим с А₁ пунктирной стрелкой. Проекция стрелки а₄ равна t₄ = 18, следовательно абсцисса узла А₄, в котором эта стрелка кончается, должна быть Т₄ = t₁ + t₄ =28. Стрелка а₅ опирающаяся на а₂ и а₃, должна начаться в узле А₃, имеющем наибольшую абсциссу из t₂ = 5 и t₃ = 15; узел А₂ соединяем с А₃ пунктирной стрелкой. Узел А₅, который заканчивается стрелкой а₅ имеет абсциссу Т₅ = t₃ + t₅ = 34. Стрелка а₆ начинается в узле А₄ и кончается в узле А₆ с абсциссой Т₆ = Т₄ + t₆ = 28 + 18 = 46. Стрелка а₇, опирающаяся на а₅, а₆, должна начинаться от узла А₆, имеющего, по сравнению с А₅, большую абсциссу; из А₅ в А₆ направляем пунктирную стрелку. Стрелка а₇ кончается в узле А₇ с абсциссой Т₇ = 46 + 8 = 54. Стрелка а₈ начинается в том же узле А₆ с абсциссой Т₆ = 46 и кончается в узле А₈ с абсциссой Т₈ = 46 + 25 = 71. Стрелка а₉ с проекцией t₉ = 30 начинается в узле А₇ и кончается в узле А₉ с абсциссой Т₉ = 54 + 30 = 84. Стрелка а₁₀, опирающаяся на а₈, начинается в узле А₈ и кончается в узле А₁₀ с абсциссой Т₁₀ = 71 + 8 = 79.

Так как работа а₉ завершается последней, то узел А₉ = А означает окончание всего комплекса работ; отметим этот узел жирным кружком и соединим с ним пунктирной стрелкой узел А₁₀ – окончание предыдущей работы а₁₀, на которую, кроме конца работ, ничто не опирается. Таким образом, временной сетевой график комплекса работ построен.

Время Т = 84 от начального узла А₀ до завершающего А = А₉ представляет собой минимальное время, за которое может быть завершён комплекс работ.

Обратим внимание на следующее обстоятельство: время Т представляет собой сумму времён исполнения не всех работ, а только некоторых из них:

Т = t₁ + t₄ + t₆ + t₇ + t₉ =10 + 18 + 18 + 8 + 30 = 84.

Работы а₁, а₄, а₆, а₇, а₉, из длительностей которых составлено время Т, называются критическими работами, а цепочка соответствующих им стрелок на сетевом графике – критическим путём (на рис. 6.3 показан двойными стрелками).

Особенность критических работ состоит в следующем: для того, чтобы было соблюдено минимальное время выполнения комплекса, каждая и них должна начинаться точно в момент, когда закончена последняя из работ, на которые она опирается, и продолжаться не более того времени, которое ей отведено по плану; малейшее запоздание в выполнении каждой из критических работ приводит к соответствующей задержке выполнения плана в целом.

Таким образом, критический путь на сетевом графике – это совокупность наиболее уязвимых, «слабых мест» плана, которые должны укладываться во временной план с наибольшей чёткостью. Что касается остальных, «некритических» работ (в нашем случае это а₂, а₃, а₅, а₈, а₁₀), то каждая из этих работ имеет известные временные резервы и может быть закончена с некоторым опозданием без того, чтобы это отразилось на сроке выполнения комплекса в целом. Резервы, соответствующие некритическим работам, легко могут быть определены по сетевому графику.

Назовём «некритической дугой» совокупность некритических работ и узлов, начинающуюся и кончающуюся на критическом пути (принимая во внимание и пунктирные стрелки). Таких дуг на рисунке 6.3 четыре:

А₀ – а₂ – А₂ – А₁,

А₀ – а₃ – А₃ – а₅ – А₅ – А₆,

А₀ – а₂ – А₂ – А₃ – а₅ – А₅ – А₆,

А₆ – а₈ – А₈ – а₁₀ – А₁₀ – А₉.

На первой из этих дуг лежит одна некритическая работа а₂; на второй – две некритические работы а₃, а₅; на третьей – две некритические работы а₂, а₅; на четвёртой – две некритические работы а₈, а₁₀.

Каждой некритической дуге соответствует определённый временной резерв, который может быть произвольным образом распределён между некритическими работами, лежащими на данной дуге. Этот резерв равен разности между суммой времён критических работ, лежащих на критическом пути, замыкающем дугу, и некритических, лежащих на самой дуге. Например, на дуге А₀ – а₂ – А₂ – А₁ лежит только одна некритическая работа а₂; на замыкающем её отрезке критического пути А₀ – а₁ – А₁ – одна критическая работа а₁; резерв времени, приходящийся на работу а₂ равен R₂ = t₁ – t₂ = 10 – 5 = 5. Следовательно, выполнение работы а₂ может быть, без ущерба для общего срока, задержано на 5 единиц времени.

На второй некритической дуге А₀ – а₃ – А₃ – а₅ – А₅ – А₆ лежат две некритические работы а₃, а₅; на замыкающем участке критического пути – три критические работы а₁, а₄, а₆. Значит общий резерв времени, приходящийся на работы а₃, а₅ равен:

R_{3, 5} = t₁ + t₄ + t₆ – (t₃ + t₅) = 10 + 18 + 18 – (15 + 19) = 12.

Резерв R_{3, 5} можно распределить между работами а₃, а₅ любым образом.

На третьей некритической дуге резерв равен:

R_{2, 5} = t₁ + t₄ + t₆ – (t₂ + t₅) = 10 + 18 + 18 – (5 + 19) = 22.

На четвёртой некритической дуге имеется резерв:

R_{8, 10} = t₇ + t₉ – (t₈ + t₁₀) = 8 + 30 – (25 + 8) = 5, который может быть произвольно распределён между работами а₈, а₁₀.

Знание критического пути на сетевом графике полезно в двух отношениях: во-первых, оно позволяет выделить из всего комплекса работ совокупность наиболее «угрожаемых», непрерывно наблюдать за ними, и, в случае надобности, форсировать их выполнение; во-вторых, оно даёт возможность в принципе ускорить выполнение комплекса работ за счёт привлечения резервов, скрытых в некритических работах, если удаётся за счёт их «безвредного» замедления перебросить часть сил и средств на более важные, критические работы.

Заметим, что на сетевом графике может быть не один критический путь, а два и более; естественно сумма времён критических работ на каждом из них должна быть одна и та же.