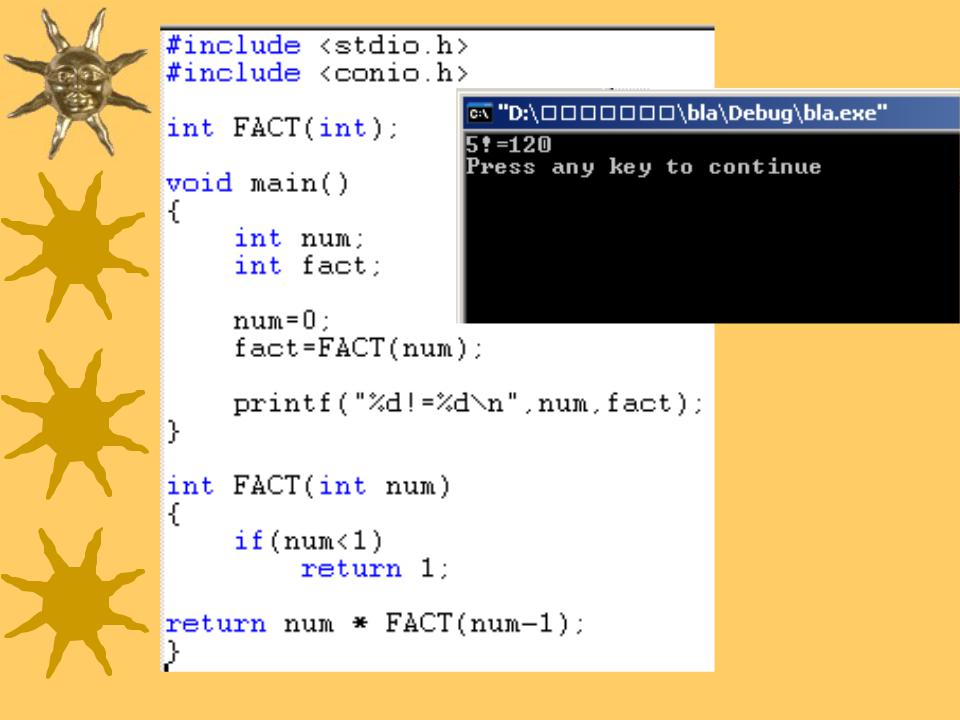
- •Рекурсивные функции
- •Введение.
- •Определение.
- •В терминах процесса и его шагов основные параметры рекурсивной функции получают дополнительный смысл,
- •Линейная, ветвящаяся рекурсии.
- •С чего начинать…
- •При разработке рекурсивного алгоритма можно выделить следующие правила:
- •Примеры использования.
- •Линейная рекурсия.

Рекурсивные функции |
Введение.
Определение.
Примеры использования…

 Введение.
Введение.
Рекурсивным называется способ построения объекта (понятия, системы), в котором определение объекта включает аналогичный объект в виде некоторой его части.
Общеизвестный пример рекурсивного изображения - предмет между двумя зеркалами - в каждом из них виден бесконечный ряд отражений.
В обычной программе мы следуем по цепочке вызовов функций, но ни разу повторно не войдем в один и тот же фрагмент, пока из него не вышли.

 Определение.
Определение.
Рекурсивная функция – это функция, которая вызывает сама себя либо непосредственно, либо косвенно с помощью другой функции.
Работу программы, содержащей рекурсивные функции, лучше всего представлять в виде некоторого процесса, в котором вызов рекурсивной функции является одним из его шагов.

В терминах процесса и его шагов основные параметры рекурсивной функции получают дополнительный смысл, который связывает их с протеканием самого процесса:
-формальные параметры рекурсивной функции |
представляют начальное состояние для текущего шага |
процесса. |
-фактические параметры рекурсивного вызова представляют начальное состояние для следующего шага, в который производится переход из текущего при рекурсивном вызове.
-автоматические переменные представляют внутренние характеристики процесса на текущем шаге его выполнения.
-внешние переменные представляют глобальное состояние всей системы, через которое отдельные шаги в последовательности могут взаимодействовать между собой.

Линейная, ветвящаяся рекурсии.
Линейная рекурсия - последовательность шагов выполняющихся линейно, т.е. рекурсивный вызов содержится в теле функции один раз.
Ветвящаяся рекурсия - последовательность шагов выполняющихся не линейно, т.е. рекурсивный вызов содержится в теле функции более одного раза, либо производится в цикле.

 С чего начинать…
С чего начинать…
Самое важное в определении рекурсии - выделить те условия, которые соблюдаются во всех точках процесса и обеспечить их справедливость от входа в рекурсивную функцию до ее рекурсивного вызова.
Очевидно, что рекурсия не может быть безусловной, в этом случае она становится бесконечной. Рекурсия должна иметь внутри себя условие завершения, по которому очередной рекурсивный вызов уже не производится.
“Категорически не приветствуется” заглядывать в следующий шаг рекурсии или интересоваться состоянием процесса на предыдущем шаге.

При разработке рекурсивного алгоритма можно выделить следующие правила:
-рекурсивная функция разрабатывается как обобщенный шаг |
процесса, который вызывается в произвольных начальных |
условиях и который приводит к следующему шагу в некоторых |
новых условиях. |
-обобщенные начальные условия шага - формальные параметры функции.
-начальные условия следующего шага - фактические параметры рекурсивного вызова.
-рекурсивная функция должна проверять условия завершения рекурсии, при которых следующий шаг процесса не выполняется.
-локальными переменными функции должны быть объявлены все переменные, которые имеют отношение к протеканию текущего шага процесса.

 Примеры использования.
Примеры использования.
Рекурсивные функции используются для обработки |
рекурсивных структур данных. |
Рекурсивным может быть любой алгоритм, в котором имеется линейная или разветвляющаяся цепочка шагов, в каждом из которых выполняется одинаковая последовательность действий.
С помощью рекурсии легко решаются задачи, связанные с поиском, основанном на полном или частичном переборе возможных вариантов. Процесс поиска разбивается на шаги, на каждом из которых выбирается и проверяется очередной элемент из множества, а алгоритм поиска повторяется, но уже для “оставшихся” данных.
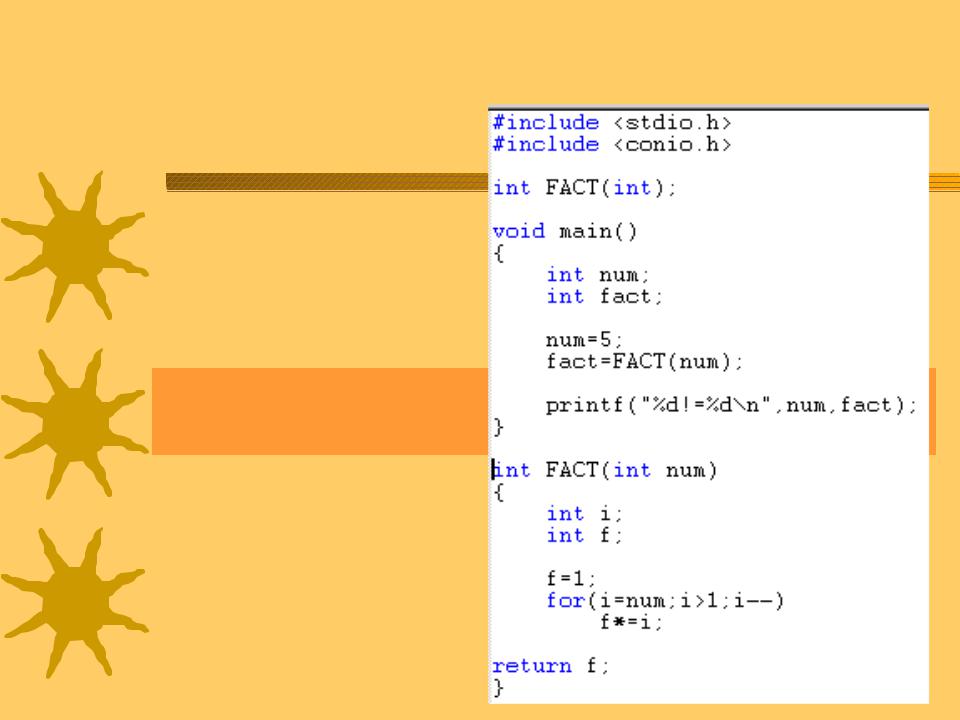
 Линейная рекурсия.
Линейная рекурсия.
Простейшим примером рекурсия, когда функция условный вызов самой становится эквивалентной
Любой циклический линейно-рекурсивный и