НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ФАКУЛЬТЕТ АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ

Кафедра Систем Сбора и Обработки Данных

Дисциплина «Сигналы и системы», 6 - й семестр

ЛАБОРАТОРНАЯ РАБОТА № 3

СПЕКТРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ

НЕПЕРИОДИЧЕСКИХ СИГНАЛОВ

Цель работы: Изучение преобразования Фурье и его свойств, понятий амплитудного и фазового спектров непериодических непрерывных по времени сигналов, приобретение практических навыков вычисления преобразования Фурье, построения графиков и анализа спектров в среде Matlab.

Задание и порядок выполнения работы

1. Ознакомьтесь с преобразованием Фурье, его свойствами, понятиями амплитудного и фазового спектров непериодического сигнала по лекционному курсу или учебной литературе, например, [3] стр. 28 – 43 или [4] стр. 31 – 49.

2. Запишите в начале отчета выражения прямого и обратного преобразования Фурье и объясните их физический смысл.

3. Аналитически определите прямое преобразование Фурье для сигнала, заданного в индивидуальном задании (Приложение 1), и постройте графики амплитудного и фазового спектров сигнала. Пример выполнения такого задания приведен в Приложении 2.

4. Напишите функцию (m - файл) вычисления дискретного преобразования Фурье (ДПФ) с синтаксисом

,

где x – N -точечный вектор значений x(0),…,x(N-1) сигнала и X- вектор значений ДПФ. В функции с использованием циклов for по n и k и встроенной функции sum() MATLAB должно вычисляться ДПФ по формуле

.

5. Вычислите с помощью функции dftsum(x) ДПФ сигнала, заданного в п.3, и постройте графики его амплитудного и фазового спектров. Соответствующий пример представлен в Приложении 3.

6. С помощью функции fft() MATLAB проведите вычисление спектра сигнала из индивидуального задания с масштабированием шкалы частот. Связь преобразования Фурье непрерывного времени (НВПФ) и дискретного преобразования Фурье (ДПФ) показана в Приложении 4.

Для сопоставления результатов, возвращаемых fft(), со значениями преобразования Фурье X сигнала возвращаемые функцией fft() значения должны быть промасштабированы, а именно , где T – длительность анализируемого сигнала, N – количество точек (размер ДПФ), Т_S - интервал отсчетов. См. Приложение 4 и Приложение 5. Пояснение. Чтобы применить процедуру fft() для представления спектра сигнала в частотной области с соответствующим масштабированием шкалы частот необходимо

• по значению интервала отсчетов (Т – длительность сигнала в сек,, N – размер ДПФ) определить максимальную частоту спектра Fmax (в Герцах) по формуле ,

• найти частотное разрешение анализа, т.е. минимальное расстояние между частотами в частотной области ,

• провести вычисления с помощью fft(),

• применить процедуру fftshift(), которая перегруппировывает выходной массив функции fft(), размещая нулевую частоту в центре спектра,

• сформировать вектор значений частот по выражению или ,

• построить график амплитудного и/или фазового спектра сигнала в зависимости от частоты.

7. Постройте в одном графическом окне графики амплитудного спектра сигнала, вычисленные в п. 3,5,6. Сопоставьте результаты. Обратите внимание, что это три способа вычисления одного и того же спектра. 8. Постройте график спектральной плотности энергии сигнала . Объясните физический смысл этой величины.

9. Используя процедуру из Приложения 6 как прототип, составьте программу для вычисления и вывода графиков фрагмента речевого сигнала во временной и частотной области (файл «MySpeech.wav» из папки «Лабораторные работы»).

Указание. Вы можете записать собственный wav – файл с помощью средств Windows и использовать его фрагмент для анализа вместо файла «MySpeech», тем самым изучив особенности спектра (тембра) собственного голоса. Это интереснее!

Прослушайте звучание сигнала. При этом для считывания wav-файла используйте команду с форматом y=wavread(‘filename’), для прослушивания - команду sound(y, Fs), для определения числа отсчетов на один канал в файле – команду N = length(y), для определения частоты дискретизации Fs записанного звукового файла - команду [y,Fs]=wavread(' filename ', 1).

Вариант последовательности команд для считывания сигнала и вычисления его ДПФ

Fs=44100; % Частота отсчетов

y=wavread('MySpeech'); % чтение сигнала

N=length(y); % длина файла в отсчетах

n1=1:N;

n=-N/2:N/2-1;

Y=fft(y(:,1)); % Вычисление ДПФ одного из каналов стереозвука

Yp=fftshift(Y); % Сдвиг ДПФ

f=n*Fs/N; % Частотная шкала

В программе используются данные по длине (числе элементов) речевого сигнала и его частоте дискретизации. Графики результатов этой части работы должны содержать вид сигнала во временной области и его амплитудный спектр. Поскольку графики содержат большое число отсчетов, полезно также увеличить и привести отдельные характерные фрагменты графиков.

10. Добавьте в программу команды вида figure(2), specgram(y(:,1),[],Fs) и постройте спектрограмму звукового сигнала. Команда specgram() без выходных параметров строит графическое изображение спектрограммы в координатах «время – частота». При этом значения амплитудного спектра отображаются с помощью цвета. Чем больше амплитуда спектральной составляющей, тем более ярким оранжевым цветом она отображается. Чем меньше амплитуда, тем более темно-голубой у нее цвет.

Проанализируйте полученную спектрограмму и сопоставьте её с данными графиков сигнала и его амплитудного спектра, построенными в п.10.

11. Составьте отчет по лабораторной работе. В отчете должны быть представлены

• титульный лист,

• название и цель работы,

• формулировки (заголовки) пунктов работы, команды и .m – файлы, графики, комментарии,

• выводы в соответствии с целью работы и её основными результатами.

Проверьте усвоение материала по контрольным вопросам, отчитайтесь в выполнении работы.

Литература

1. Щетинин Ю.И. Анализ и обработка сигналов в среде MATLAB: учеб. пособие/ Ю.И. Щетинин. – Новосибирск: Изд-во НГТУ, 2011. – 115 с.

2. Теория и обработка сигналов. Методические указания к решению задач и упражнений. / Составитель Щетинин Ю.И. - Новосибирск: Изд-во НГТУ, 2007. – 108 с.

3. Голышев Н.В., Щетинин Ю.И. Теория и обработка сигналов.: Уч. пособие.- Новосибирск. Изд-во НГТУ, 1998 - ч.1.

4. Сергиенко А.Б. Цифровая обработка сигналов. СПб: Питер, 2003.

Web – ресурсы

1. http://www.jhu.edu/~signals/ctftprops-mathml/index.htm

2. Tos_Demo/nperiodic/start.html

Контрольные вопросы и упражнения

1. Запишите формулы прямого и обратного преобразования Фурье и объясните их физический смысл.

2. Как связаны преобразование Фурье и ряд Фурье? Получите и объясните соответствующее выражение.

3. Сформулируйте условия существования (сходимости) преобразования Фурье.

4. Что такое амплитудный спектр непериодического сигнала и каковы его особенности? Объясните физический смысл амплитудного спектра.

5. Как по спектральной плотности сигнала найти вклад определенной частоты в функцию сигнала?

6. Приведите определение фазового спектра сигнала. Что он выражает?

7. Как по спектру Фурье найти сам сигнал как временную функцию?

8. Определите преобразование Фурье, амплитудный и фазовый спектры сигнала . Постройте графики спектров в MATLAB. Используя свойство изменения масштаба, получите преобразование Фурье функции . Как соотносятся сигналы и их спектры?

9. Дано дифференциальное уравнение, связывающее вход x(t) и выход y(t) системы 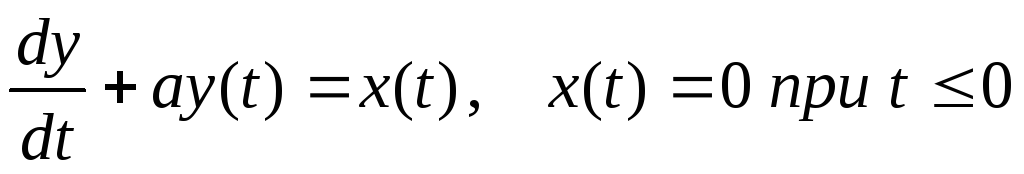. С использованием свойства дифференцирования найдите преобразование Фурье этого уравнения. Определите отношение преобразований Фурье левой и правой части, т.е. . Постройте в Matlab графики модуля и фазы этого отношения от частоты для . Дайте интерпретацию физического смысла функций на графиках.

10. Используя свойства линейности и временного сдвига преобразования Фурье, постройте амплитудный спектр сигнала, основываясь на преобразовании Фурье прямоугольного импульса.

11. С помощью функции fourier() Matlab найдите преобразование Фурье сигнала . Постройте амплитудный спектр этого сигнала. 12. Постройте график энергетического спектра сигнала из предыдущего пункта (используйте теорему Парсеваля).

13. Какова связь между длительностью сигнала и шириной его спектра? Как это можно обосновать?

14. В среде Matlab найдите преобразование Фурье сигнала s(t) и постройте график его амплитудного спектра с масштабированием шкалы частот

Объясните характер полученного результата.

15. Объясните содержание и метод оценки спектра сигнала с помощью дискретного преобразования Фурье (fft).

Приложение 1. Индивидуальные задания

1. Косинусоидальный импульс .

2. Несимметричный треугольный импульс

Указание. Используйте свойство частотного сдвига преобразования Фурье.

3. Два прямоугольных импульса

.

Указание. Используйте теорему (свойство) линейности и свойство сдвига.

4. Односторонний треугольный импульс

5. Сигнал вида Указание. Используйте свойство частотного сдвига преобразования Фурье.

6. Односторонний экспоненциальный сигнал

7. Прямоугольный импульс

.

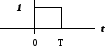8. Синусоидальный импульс

9. 

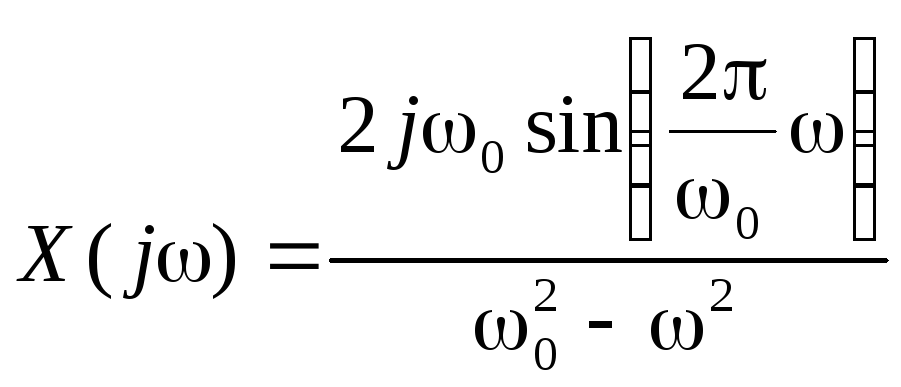
10. Гауссовский импульс

11. Двусторонний экспоненциальный сигнал .

12. Косинусоидальный импульс .

13. Косинусоидально – затухающий сигнал

Приложение 2

Сигнал – симметричный треугольный импульс

Преобразование Фурье сигнала

% Файл – сценарий построения амплитудного и фазового спектров

T=10;

dt=0.1; % задание интервала отсчетов

t=-T:dt:T; % шкала времени

A=5; s=A*(1-abs(t)/T); % определение сигнала

% Дополнение нулями для повышения частотного разрешения

s1=[zeros(1,4*length(t)),s, zeros(1,4*length(t))];

T1=9*length(s1)*dt; % Длительность сигнала, дополненного нулями

df=1/T1; Fmax=1/dt; % задание частотной шкалы

f=-Fmax:df:Fmax;

S=A*T*sinc(f*T).^2; % выражение комплексного спектра

% построение графиков сигнала и спектров

subplot(311), plot(t,s)

title('Cигнал')

subplot(312), plot(f,abs(S))

xlim([-0.4 0.4])

set(gca,'FontName', 'Times New Roman Cyr', 'FontSize', 10)

title('Амплитудный спектр')

subplot(313), plot(f,angle(S))

title('Фазовый спектр')

Приложение 3. Пример вычисления ДПФ с помощью функции dftsum()

% Вычисление спектра и построение его графиков

T=10; dt=1; % Определение интервала времени

t=-T:dt:T;

N=length(t);

A=5; s=A*(1-abs(t)/T); % задание сигнала

% Добавление нулей к сигналу для увеличения частотного разрешения

S=[zeros(1,2*N) s zeros(1,2*N)];

df=1/(dt*length(S)); Fmax=1/dt; % определение частотной шкалы

f=-(Fmax-df)/2:df:Fmax/2;

y1=dftsum(S); y1p=fftshift(y1); % вычисление и сдвиг ДПФ

% Построение графиков сигнала и его спектров

figure(1), subplot(311), plot(t,s)

% set(gca,'FontName','Arial Cyr', 'FontSize',12)

title('Сигнал')

subplot(312), plot(f,abs(y1p),'o-')

% set(gca,'FontName','Arial Cyr', 'FontSize',12)

title('Амлитудный спектр'),grid

subplot(313), plot(f,angle(y1p)),

% set(gca,'FontName','Arial Cyr', 'FontSize',12)

title('Фазовый спектр')

Xlabel('Частота, Гц'), grid

Графики

Приложение 4. Связь преобразования Фурье непрерывного времени (НВПФ) и дискретного преобразования Фурье (ДПФ).

Выражение прямого ДПФ для последовательности x[n] из N чисел

Пусть из непрерывного по времени сигнала x(t) берутся N отсчетов с интервалом T_S и этот сигнал равен нулю за пределами интервала [0, (N-1)T_S].

Преобразование Фурье такого сигнала

.

Значения НВПФ на частотах , T_SN – продолжительность (длина) сигнала.

Следовательно, НВПФ сигнала на частотах равно ДПФ, умноженному на значение интервала отсчетов Т_S. Аппроксимация тем точнее, чем меньше интервал отсчетов T_S, в пределах которого сигнал не должен существенно измениться.

Приложение 5

% Процедура сопоставления преобразования Фурье

% и его вычисления с помощью функции fft()

T=8;% длительность процесса

N=128; % число точек

Ts=T/(N-1); % интервал отсчетов

t=0:Ts:T; % временной интервал

tau=2; % длительность импульса

x=rectpuls(t,tau); % генерирование прямоугольного импульса

figure(1);

subplot(311), plot(t,x) % график сигнала

title(' График сигнала')

Fmax=1/Ts; % максимальная частота

df=1/T; % частотное разрешение

f=-Fmax/2:df:Fmax/2; % частотная шкала

X=fft(x,N); % БПФ сигнала

Xp=fftshift(X); % частотный сдвиг

A=abs(Xp);

subplot(312), plot(f,A*Ts)

title('fft- Амплитудный спектр сигнала')

S=sinc(f*tau/2)*tau/2; % преобразование Фурье сигнала

% график

subplot(313), plot(f, abs(S))

xlabel(' Частота, Гц')

title(' Амплитудный спектр сигнала ')