Принцип Ландауэра

Преобразование информации связано с затратой энергии. Найдем минимальную энергию, необходимую для стирания бита информации, или для получения бита.

Ящик, содержащий одну частицу, имеет в середине съемную перегородку, показанную на рис. 2.12, а. Частица находится в левой половине ящика, затем перегородка вынимается, что соответствует рис. 2.12, б. Найдем изменение энтропии системы и минимальное количества энергии, связанной с этим процессом.

Для изолированных объемов фазовое пространство системы распадается на независимые подпространства. Формула Больцмана для энтропии (2.101)

получает вид

, (П.3.16)

где – вероятность обнаружения частицы в объеме с номеромi. Соответствующие вероятности приведены на рисунке.

а б

Рис. 2.12. Частица в сосуде с перегородкой (а), и без нее (б)

Для состояний на рис. 2.12 а и б, находим

,

.

При изотермическом переходе между состояниями увеличение энтропии пропорционально количеству рассеянного тепла

,

откуда

. (П.3.17)

Состояние а соответствует биту информации о частице в системе. Переход к состоянию б приводит к потере этой информации. В результате выполняется принцип Ландауэра (1961 г.) – стирание бита информации приводит к рассеянию энергии в окружающую среду с температурой Т. При получаем 0,0178 эВ. Другие формулировки для

– энергия, затрачиваемая на создание бита информации;

– высота барьера, необходимая для разделения двух состояний электрона, или другого носителя информации;

– нижний предел для энергии реального процесса преобразования информации, как показано экспериментально в 2012 г. (Nature 483, 187).

До Ландауэра результат (П.3.17) получил в 1949 г. фон Нейман – американский математик, заложил принципы работы компьютера и математические основы квантовой механики.

Рольф Ландауэр (1927–1999) Джон фон Нейман (1903–1957)

Статистический интеграл поступательного движения

Идеальный газ из N атомов находится в объеме V при температуре Т. Найдем статистический интеграл поступательного движения, внутреннюю энергию и давление газа.

1. Статистический интеграл атома

Используем

,

,

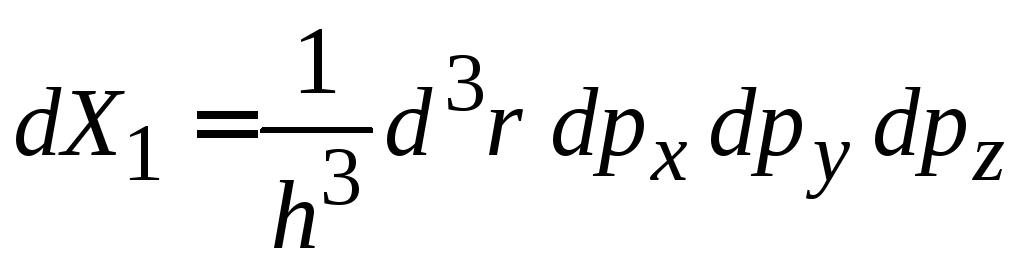и гамильтониан поступательного движения атома

.

Подстановка дает

.

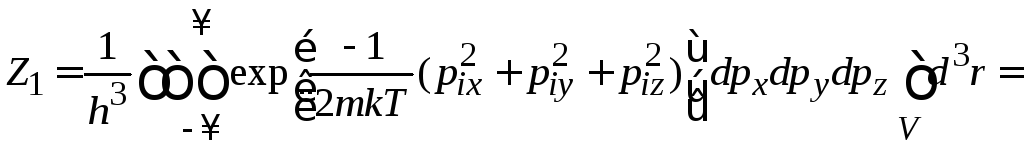
Учтено, что координаты и разные проекции импульса разделены. Использовано

.

Интеграл в квадратных скобках является интегралом Пуассона

,

и равен . Получаемстатистический интеграл поступательного движения частицы (2.22)

. (П.3.1)

С учетом

находим статистический интеграл поступательного движения газа

.

2. Внутренняя энергия газа

Вычисляем (2.26)

.

Из находим

.

При используем формулу Стирлинга

,

тогда

.

С учетом (П.3.1)

,

получаем

, ,

тогда

,

. (П.3.1а)

Из (2.26)

получаем

,

.

Результат совпадает с выражением, найденным из микроканонического распределения, а также с известной формулой термодинамики идеального газа. Это позволяет отождествить k с постоянной Больцмана.

3. Давление газа

Из (2.34) и (П.3.1а) находим

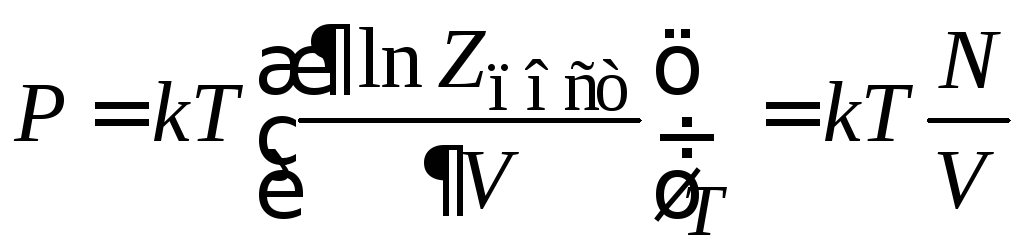
и получаем уравнение идеального газа .