Гильбертово пространство с непрерывным базисом

Базис ортов

,

где . Номер ортаk пробегает непрерывные значения в интервале .

Условие ортонормированности базиса. Непрерывность k приводит к замене символа Кронекера в условии (0.6) на дельта-функцию

, (0.11)

где – дельта-функция.

Разложение функции по непрерывному базису

, (0.12)

где проекция на орт

. (0.13)

Совпадение спектров функций означает равенство функций.

Доказательство (0.13)

Подставляем (0.12) в (0.13)

.

Меняем порядок интегрирований по x и k, считая интегралы существующими. Используем условие ортонормированности и фильтрующее свойство дельта-функции

.

Получено тождество и это доказывает формулу (0.13).

Условие полноты базиса

. (0.14)

Проверить самостоятельно, что подстановка (0.13) в (0.12) с учетом (0.14) дает тождество.

Теорема Парсеваля

. (0.15)

Доказать самостоятельно с помощью (0.11) и (0.12), или с помощью (0.13) и (0.14).

Рассмотрим непрерывный базис, построенный из гармонических функций.

Преобразование фурье

Для наблюдателя на Земле планета, от греч. πλανήτης – «блуждающая», совершает неравномерное и иногда даже возвратное движение по небу. Древнегреческий математик Аполлоний представил сложное движение планеты в виде суммы равномерных вращений по окружностям – эпициклам в III в до н.э.

Аполлоний Пергский – (ок. 262 – ок. 190 до н.э.)

Проекция равномерного вращения по окружности описывается гармоническими функциями – синусом, косинусом и экспонентой с мнимым показателем. Идея Аполлония через 2 тысячи лет была применена к функциям французским математиком Фурье. Он разложил функцию по гармоническим составляющим в 1807 г. Переход от функции к набору ее проекций, или спектру, называется преобразованием Фурье.

Жан Батист Жозеф Фурье (1768–1830)

Преобразование Фурье использует ортонормированный базис гармонических функций.

Бесконечномерный базис гармонических функций

, ;.

Орт является решением волнового уравнения Гельмгольца

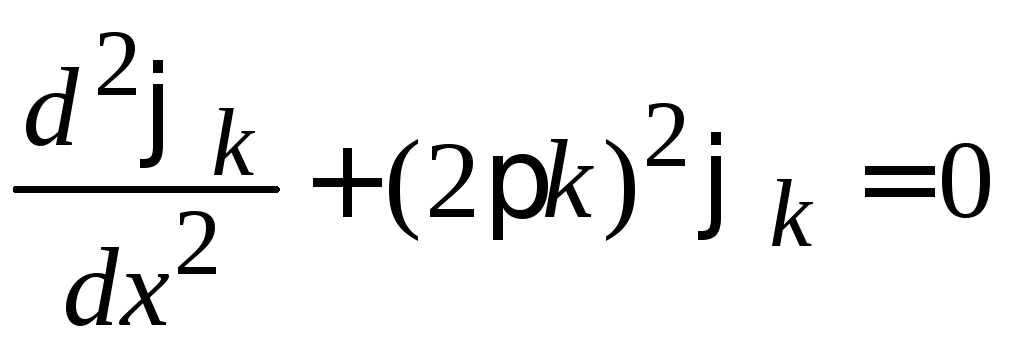
и описывает плоскую волну

,

распространяющуюся вдоль оси x с волновым число k.

Герман Гельмгольц (1821–1894)

Базис с непрерывным спектромудовлетворяет:

условию ортонормированности

,

и условию полноты

.

Интегрирование выполнено при помощи формул, которые будут доказаны в разделе «Дельта-функция».

Преобразование Фурье функции является ее разложением по базису , спектр функциивыражается подобным преобразованием:

, (1.1)

. (1.2)

Использовано:

–оператор Фурье, действующий на функцию с аргументом x, находящуюся в скобках , и дающий функцию, зависящую отk;

–оператор обратного преобразования Фурье, действующий на функцию с аргументом k, находящуюся в скобках , и дающий функцию, зависящую отx;

–Фурье-образ или спектр функции ;

k и x – Фурье-сопряженные переменные, – безразмерная;

–ядро преобразований, не зависящее от преобразуемой функции.

Преобразование Фурье технически реализуется, например, колебательным контуром входного каскада радиоприемника, или телевизора. Выделенная полоса спектра далее усиливается. Рассмотрим примеры преобразования Фурье, использующие оптические устройства.