Экзамен микроэлектроника / Лекции / 13. ЭСЛ_статика_2

Статические характеристики ЭСЛ. Продолжение

Выходная характеристика.

Рассмотрим выходную характеристику элемента ЭСЛ. Так как элемент может находиться в двух логических состояниях выхода и может использоваться с подключенными резисторами и без них, то необходимо рассмотреть четыре различные выходные характеристики. При этом по-прежнему будем считать, что для транзистора, работающего в активном режиме , а если , то транзистор закрыт (все токи равны нулю).

Для логического элемента с состоянием «1» на выходе с подключенным резистором расчетная схема имеет вид, показанный на рисунке:

Для данной схемы справедливы следующие очевидные соотношения:

;

;

;

Тогда выражение для выходного тока перепишется в виде:

Это уравнение прямой, проходящей через точку с координатами:

Выходное сопротивление тогда будет равно:

Учитывая, что , из выражения для заданной точки прямой получим численные значения:

При транзистор закрыт и расчетная схема приобретает вид:

Из рисунка видно, что .

Это уравнение прямой, проходящей через точку .

Выходная характеристика для рассмотренного случая приведена на рисунке. Она имеет два линейных участка. Из совместного решения уравнений прямых можно определить точку их пересечения, т.е. границу двух режимов транзистора эмиттерного повторителя:

Подставив числовые значения получим .

Рассмотрим теперь случай логического нуля на выходе. При наличии резистора схема имеет вид:

Транзистор здесь работает в активном режиме и является источником тока для транзистора эмиттерного повторителя. Для данной схемы справедливы следующие соотношения:

;

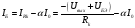Учитывая, что и можно записать:

.

Это уравнение прямой, проходящей через точку .

Здесь ток при 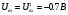. Выходное сопротивление вычисляется точно также, как и в предыдущем случае.

Численные расчеты дают значение выходного напряжения для этой точки, равное . При транзистор закрыт расчетная схема снова принимает вид, как на рисунке:

Решая совместно соответствующие уравнения прямых, находим точку их пересечения:

.

Аналогичным образом строятся выходные характеристики при отсутствии резистора

5