теория / 54 ВОПРОС

54. Определенный интеграл с переменным верхним пределом.

Если f(x) интегрируема на , то она интегрируема и на , где x – любое значение из . Интеграл , , (1)

называется определенным интегралом с переменным верхним пределом и является функцией верхнего предела x. Переменная интегрирования обозначена буквой t, чтобы различать ее и верхний предел x. Геометрический смысл функции : это площадь криволинейной трапеции aAMN (заштрихованной) (рис.1).

Т. Если f(t) непрерывна в точке t=x, то в этой точке существует производная функции , причем

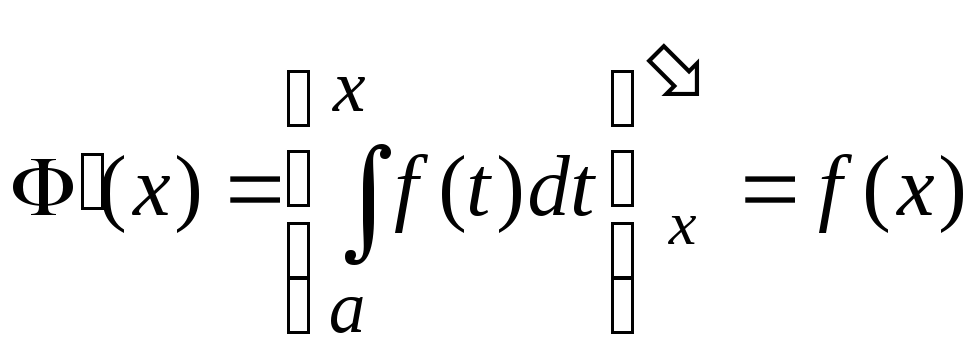. (4)

Т. Если f(x) непрерывна на отрезке , то производная от интеграла из равенства (1) по переменному верхнему пределу всюду в существует и равна подынтегральной функции, в которой вместо переменной интегрирования подставлено значение верхнего предела, т.е. имеет место равенство (4) .

Данная теорема означает, что для непрерывной на отрезке функции f(x) всегда существует первообразная, и примером ее является определенный интеграл (1) с переменным верхним пределом:

.

Таким образом, во-первых, теорема является одновременно и теоремой о существовании первообразной у каждой непрерывной функции f. Во-вторых, она устанавливает связь между неопределенным и определенным интегралами.