теория / 59 ВОПРОС

59.Вычисление площадей плоских фигур в прямоугольной системе координат.

Пусть непрерывная кривая задана в прямоугольных координатах x,y уравнением y = f(x) на отрезке [a,b] и . Тогда площадь S прямоугольной трапеции, ограниченной кривой y = f(x), осью Ox и прямыми x = a, x = b (рис.1,a), определяется формулой 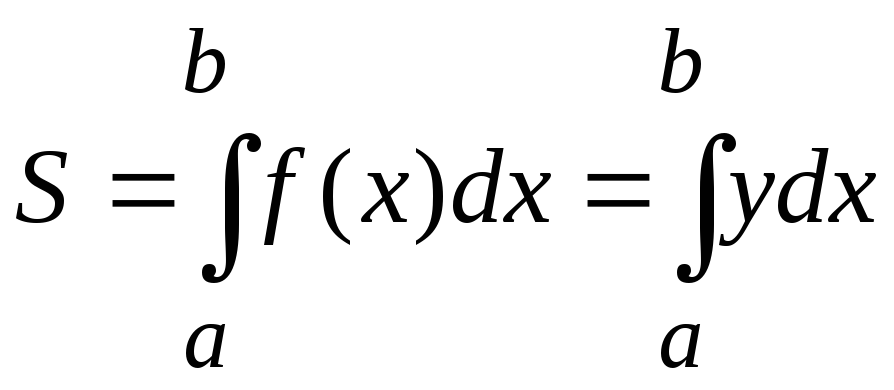. (1)

Пусть криволинейная трапеция ограничена кривой (причем ), осью ординат Oy и прямыми y = c, y = d (рис.1,б). Тогда ее площадь S определяется формулой: . (2)

Если и , то в формулах (1), (2) перед интегралами добавляется знак минус.

Если подынтегральная функция f(x) конечное число раз меняет знак на отрезке , то интеграл (1) равен алгебраической сумме площадей соответствующих криволинейных трапеций, лежащих над осью абсцисс (берущихся со знаком «+») и под этой осью ( со знаком «–»)

Чтобы получить общую площадь заштрихованной фигуры отрезок интегрирования следует разбить на частичные отрезки, на каждом из которых функция f(x) сохраняет знак, и применить формулу (1) с учетом сделанного замечания. Тогда

.

Если фигура ограничена двумя непрерывными кривыми и и двумя вертикалями x = a и x = b, причем , то ее площадь S определяется формулой. (3)

Если кривая задана в параметрической форме уравнениями , , где , то площадь S криволинейной трапеции, ограниченной этой кривой, осью Ox и прямыми x = a, x = b выражается формулой (при , ) , (4) получаемой из формулы (1) заменой переменной , , . Пределы интегрирования определяются из уравнений , .