теория / 61 ВОПРОС

61.Вычисление длины дуги кривой

l=(x²+y²)^1/2

dl=(1+(y)²)^1/2dx

Длина дуги плоской кривой, заданной параметрически

Пусть кривая задана параметрически уравнениями , , , где – непрерывно дифференцируемые на функции.

Для вычисления длины s дуги кривой применим формулу (3), предварительно выполнив замену переменной:

, .

Имеем

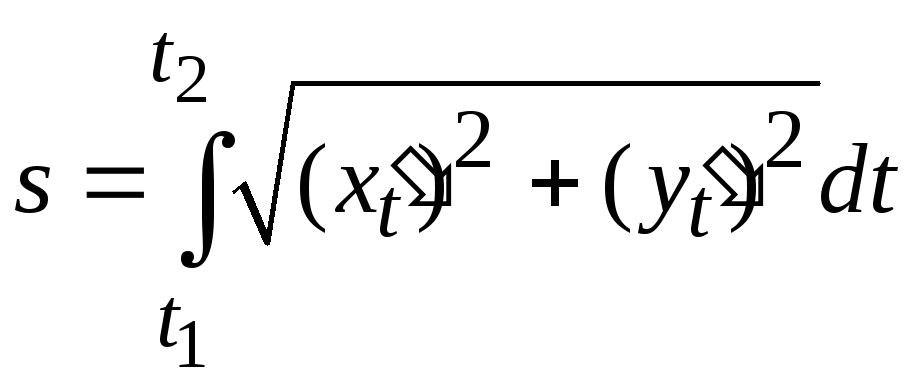или . (4)

Длина дуги пространственной кривой

Пусть пространственная кривая задана параметрическими уравнениями , , , , где x(t), y(t), z(t) – непрерывные функции, имеющие непрерывные производные на отрезке . Тогда длина дуги этой кривой выражается формулой

. (5)

Длина дуги кривой в полярной системе координат

Пусть кривая задана в полярной системе координат уравнением , где функция непрерывно дифференцируема на отрезке . Допустим, что и непрерывны на отрезке . Покажем, что данную кривую можно задать параметрически. Совместим декартову систему координат с полярной, поместив начало (0,0) в полюс, а ось абсцисс направим по полярной оси. Тогда между декартовыми и полярными координатами существует следующая связь:

Учитывая, что , получаем

Последние равенства, очевидно, можно рассматривать как параметрические уравнения кривой с параметром . Для вычисления длины дуги применим формулу (4). Вычислим производные от x и y по параметру :

.

Поэтому из формулы (4) получаем:

, (6)

где – значения полярного угла, соответствующие концам дуги.

Дифференциал длины дуги

Длина дуг кривой определяется формулой

,где . Допустим, что в этой формуле нижний предел интегрирования остается постоянным, а верхний предел изменяется. Обозначая верхний предел буквой x, а переменную интегрирования буквой t, получим, что длина дуги будет функцией верхнего предела x:

.

функция s(x) является дифференцируемой, а ее производная определяется формулой .

Следовательно, дифференциал дуги или .

Поскольку , то , т.е. .

Эта формула представляет собой аналог теоремы Пифагора.