теория / 53 ВОПРОС

53.Условие интегрируемости функций. Основные свойства определенного интеграла.

Условия интегрируемости функции на отрезке – это условия существования определенного интеграла . При определении его как предела интегральной суммы предполагалось, что функция ограничена на отрезке .

Необходимое условие интегрируемости функции

Покажем, что условие ограниченности функций на отрезке является необходимым условием интегрируемости функций, т.е. справедлива следующая теорема.

Т. Если существует, то функция ограничена на отрезке .

Ограниченность является необходимым, но не достаточным условием интегрируемости функции на отрезке , Существуют ограниченные функции, не являющиеся интегрируемыми.

Достаточные условия интегрируемости функции

Т. Если функция непрерывна на отрезке [a, b], то она интегрируема на этом отрезке, т.е. существует

Т. Если функция ограничена на отрезке [a, b] и непрерывна на нем всюду, кроме конечного числа точек разрыва первого рода, то она интегрируема на этом отрезке.

Т. Если функция монотонна и ограничена на отрезке [a, b], то она интегрируема на [a, b].

Свойства определенного интеграла, выражаемые равенствами

1. Если нижний и верхний пределы интегрирования равны , то интеграл равен нулю: .

2. При перестановке пределов интегрирования определенный интеграл меняет знак на противоположный:

3.

4. Если функция f(x) интегрируема на отрезке [a, b], то и функция , где k – постоянная, также интегрируема на [a, b], причем ,

т.е. постоянный множитель можно выносить за знак определенного интеграла.

5. Если функции f(x) и g(x) интегрируемы на [a, b], то также интегрируема на [a, b], причем

.

6. Аддитивность определенного интеграла. Если существуют интегралы и , то существует также интеграл (и обратно) и для любых чисел a, b, c .

7. Если функция f(x) не меняет знак на , то определенный интеграл сохраняет ее знак, т.е. если , то , , .

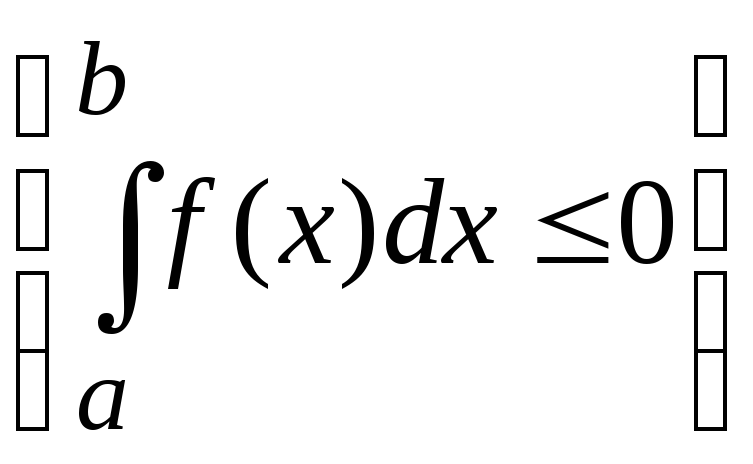8. Монотонность определенного интеграла. Если интегрируемые функции и удовлетворяют неравенству , то , .

9. Оценка интеграла. Если f(x) интегрируема на и , то , .

10. (о среднем значении для непрерывной функции). Если функция f(x) непрерывна на отрезке , то существует такая точка , что ,

т.е. определенный интеграл от непрерывной функции равен произведению значения подынтегральной функции в некоторой промежуточной точке отрезка интегрирования и длины b–a этого отрезка.

Число , определяемое по формуле , называется интегральным средним значением функции f(x) на отрезке .