Алгоритм метода факторизации

1. Оцениваем тип уравнения – гипергеометрическое (5.4), или обобщенное гипергеометрическое (5.5). В других случаях приводим уравнение к стандартному виду путем замены аргумента и/или функции.

2. Сравниваем коэффициенты уравнения с коэффициентами в (5.5) или в (5.4) и находим функцию , параметры, функциии.

3. Граничные условия (5.10) доопределяют δ и η, или A и B.

4. Весовую функцию находим из (5.8).

5. Решение уравнения получаем из (5.7) или (5.9).

6. Условие ортонормированности находим из (5.11).

7. Вычисляем из (5.16–17). Из (5.15) или (5.18) находим производящую функцию.

Рассмотрим примеры решения уравнений. Полученные результаты будут использоваться далее для детального исследования полученных решений и их применения к конкретным физическим и техническим системам.

Пример 1 Уравнение Эрмита

1. Уравнение относится к гипергеометрическому типу, поскольку

, ,.

2. Уравнение и коэффициенты сравниваем с (5.4)

, , , , ,

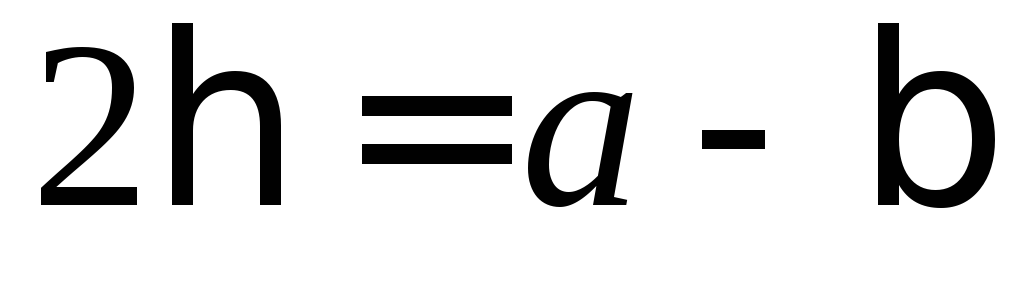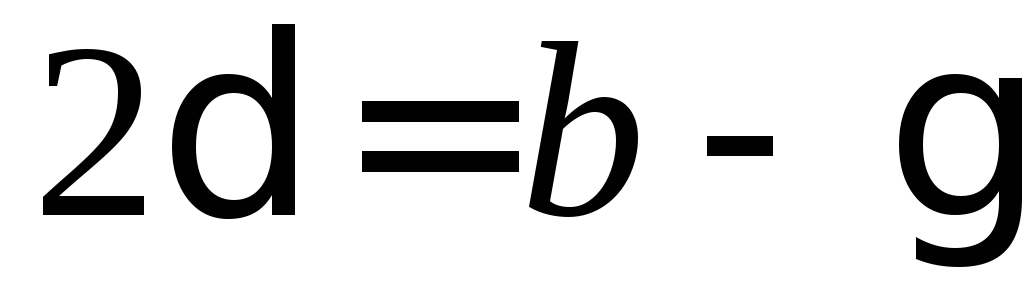получаем систему алгебраических уравнений

,

,

.

Находим параметры

, ,

, ,

и функции

, .

3. Из (5.10)

с учетом

получаем границы области определения решений

, .

4. Из (5.8)

находим весовую функцию

. (П.3.1)

5. Из (5.9)

получаем решение уравнения в форме Родрига

. (П.3.2)

При получаем решение, называемоеполином Эрмита:

. (П.3.3)

6. Из (5.11) и (5.13)

, , ,

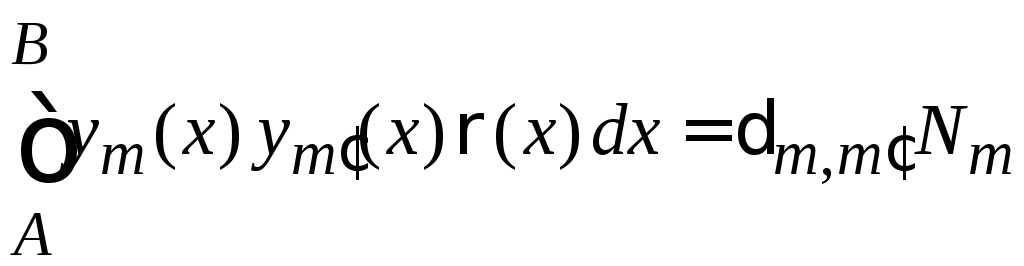с учетом

, ,

, ,

,

,

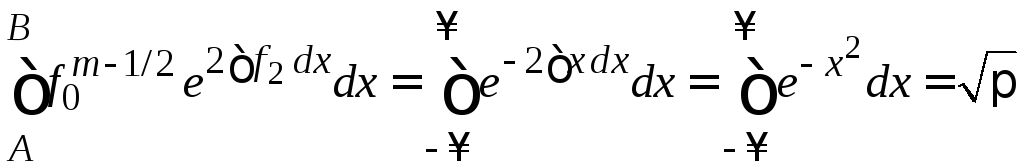находим условие ортонормированности

. (П.3.4)

7. Из (5.16)

с учетом находим

.

Из (5.17)

, ,

С учетом получаем производящую функцию

,

. (П.3.5)

Пример 2 Уравнение линейного гармонического осциллятора в квантовой механике

.

1. Уравнение относится к обобщенному гипергеометрическому типу с коэффициентами

, ,.

2. Сравнение с (5.5)

дает

,

,

,

тогда

,

,

, ,,.

Из (5.6)

, , ,

получаем систему алгебраических уравнений и находим

, ,

,

.

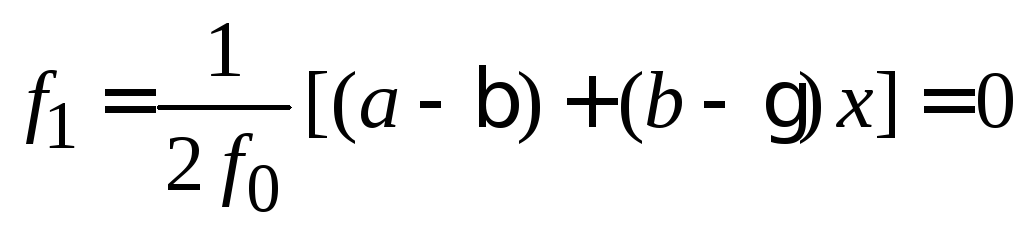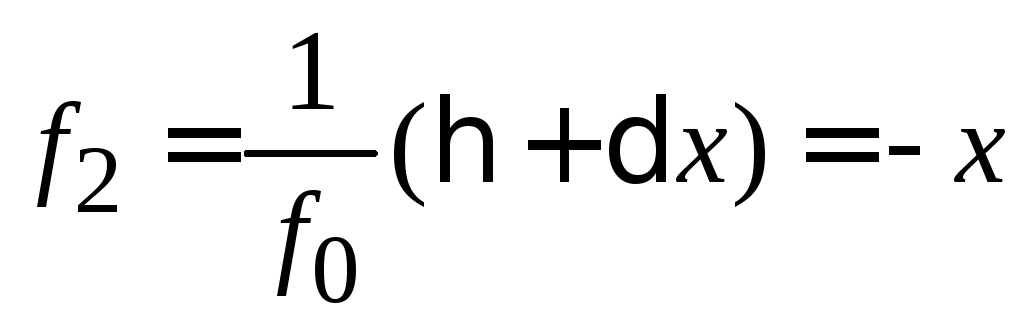3. Из (5.10)

следует границы интервала области определения решения

, .

4. Из (5.8) получаем весовую функцию

.

5. Из (5.7)

находим решение

. (П.3.6)

где – полином Эрмита.

6. Из (5.11) и (5.13)

, , ,

с учетом

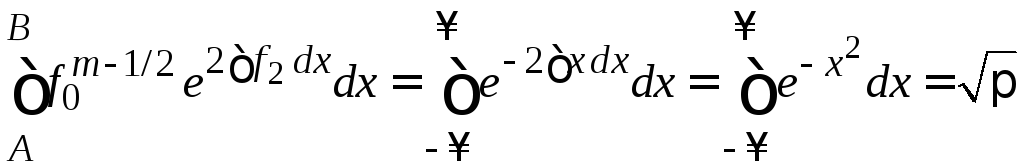
находим условие ортонормированности

, (П.3.7)

7. Из (5.16)

находим

.

В (5.15)

подставляем

, ,

получаем производящую функцию

,

. (П.3.8)