Пример 4
В
квантовой статистической теории газа
фермионов – частиц с полуцелым спином
(электроны, дырки, атомы и др.), требуется
вычислить интеграл
 ,
,
 .
.
Выполняется
 .
(П.2.19)
.
(П.2.19)
Из
(П.2.19) получаем
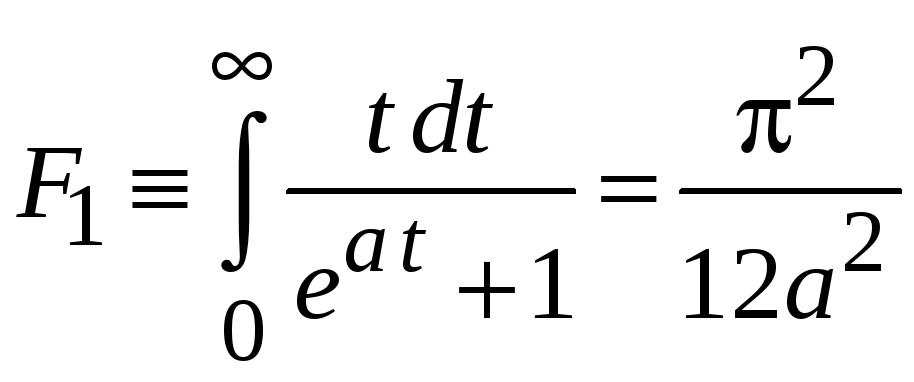 ,
,
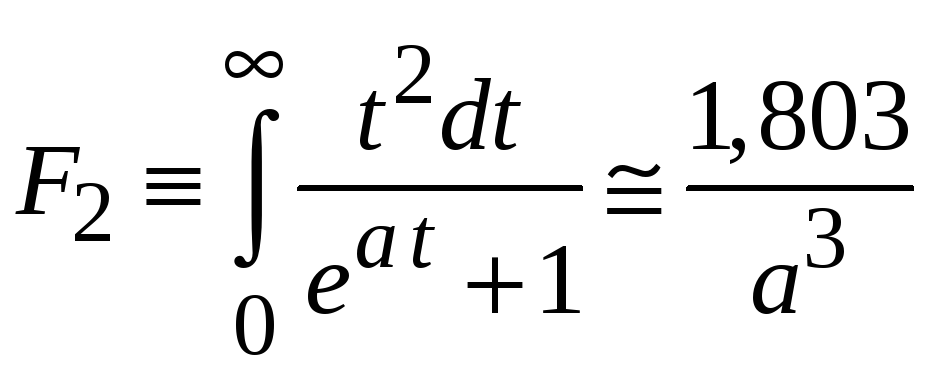 ,
,
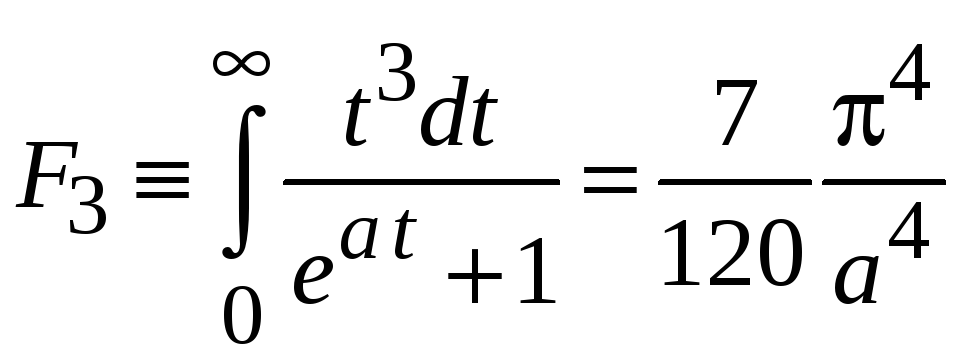 .
.
Доказательство
(П.2.19)
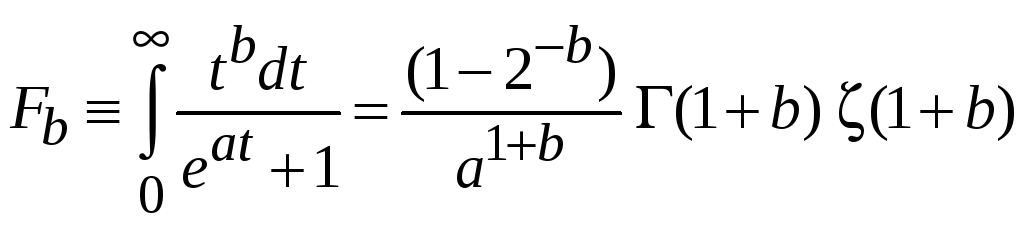 .
.
Замена
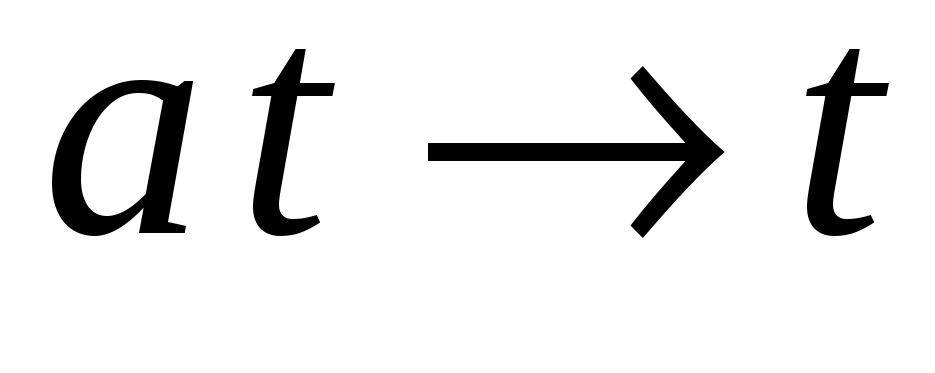 дает
дает
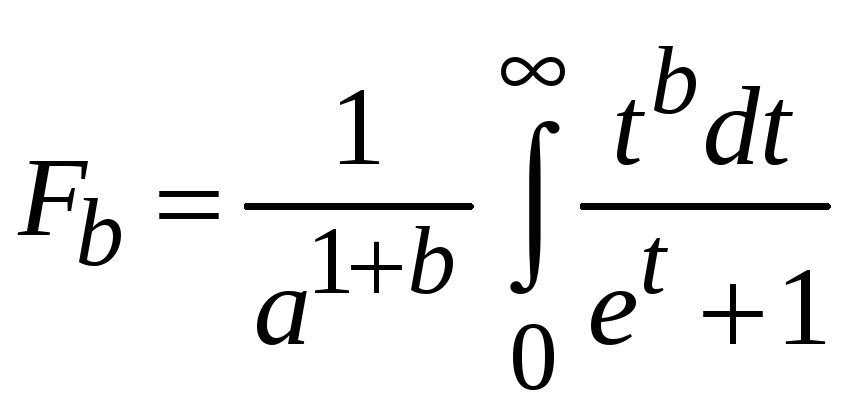 .
.
Используем
 ,
,
получаем
 .
.
Функцию
 разлагаем в ряд Маклорена
разлагаем в ряд Маклорена
 ,
,
при
 находим
находим
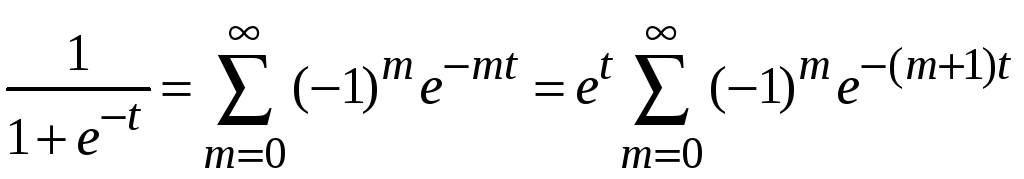 .
.
Подстановка
в интеграл дает
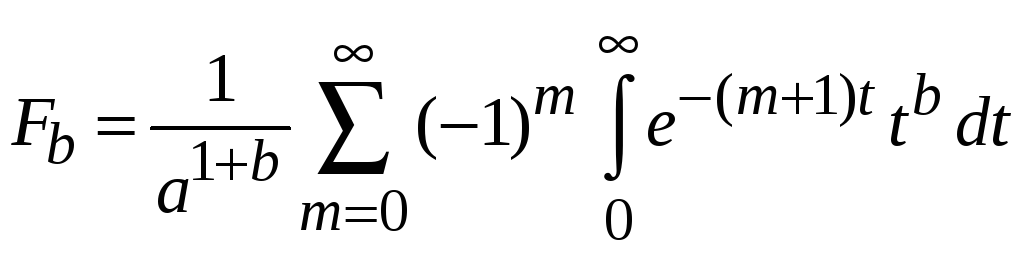 .
.
Используем
(4.8)
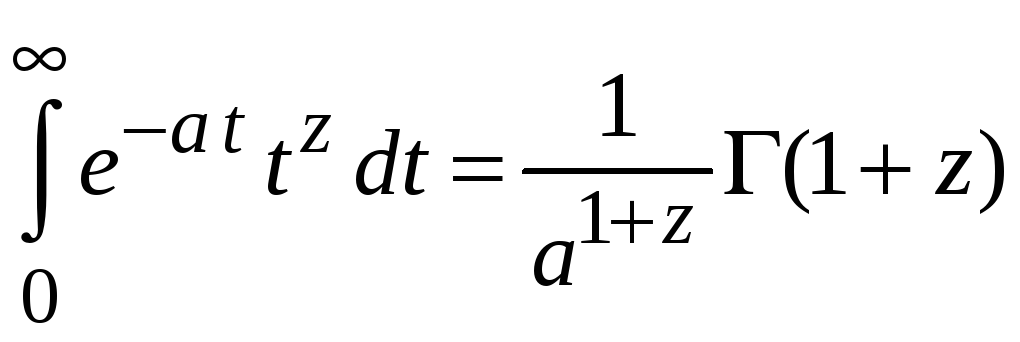
при
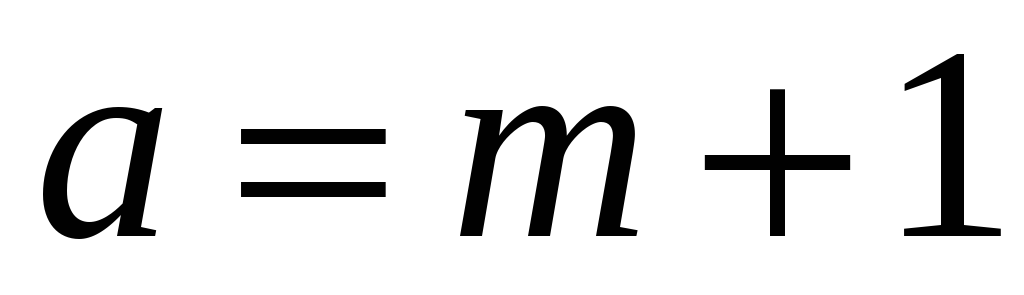 ,
,
 ,
и получаем
,
и получаем
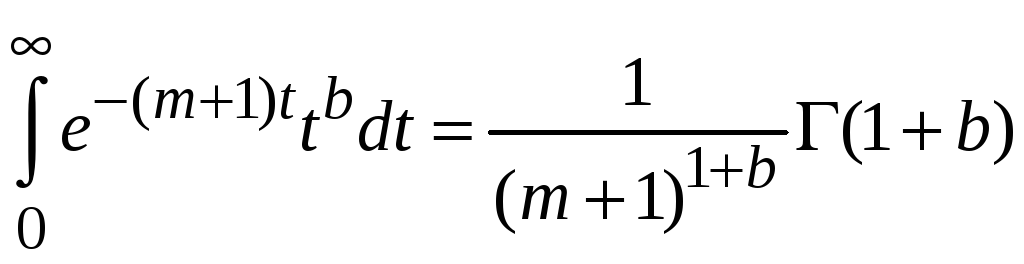 .
.
В
результате
 .
.
Сумма
выражается через дзета-функцию (см.
пример в учебнике)
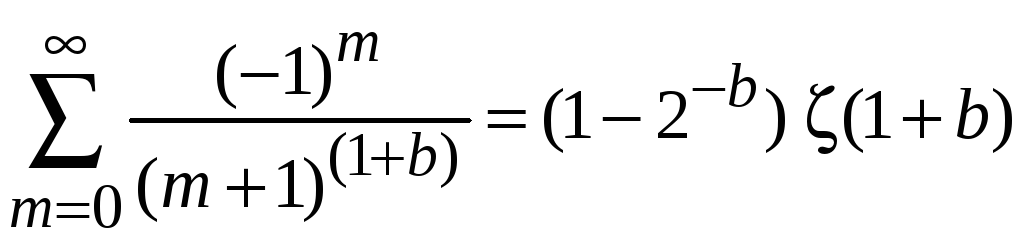 ,
(П.2.21)
,
(П.2.21)
тогда
получаем (П.2.19)
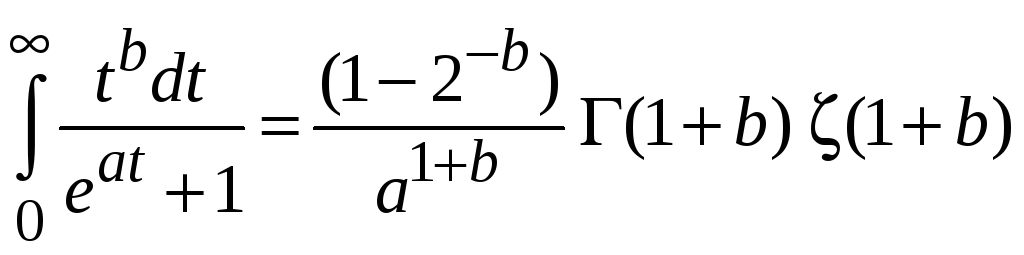 .
.
При
 в интеграле
в интеграле
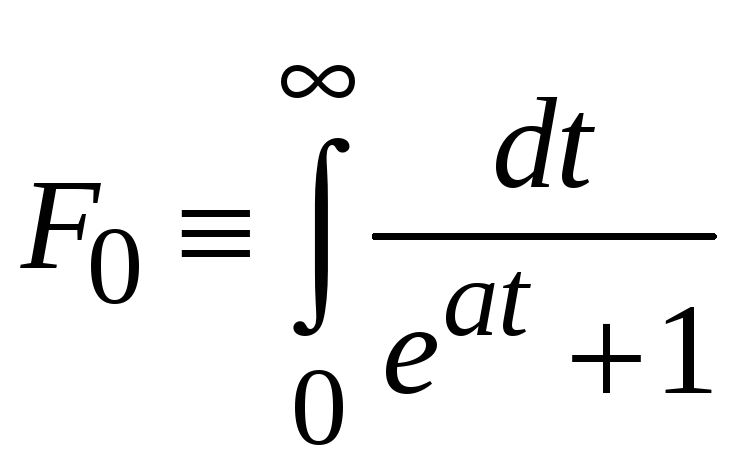
заменяем
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
и
находим
 ,
,
где
использовано
 ,
,
в
результате
 .
(П.2.20)
.
(П.2.20)
90


 ,
,
 .
(П.2.19)
.
(П.2.19)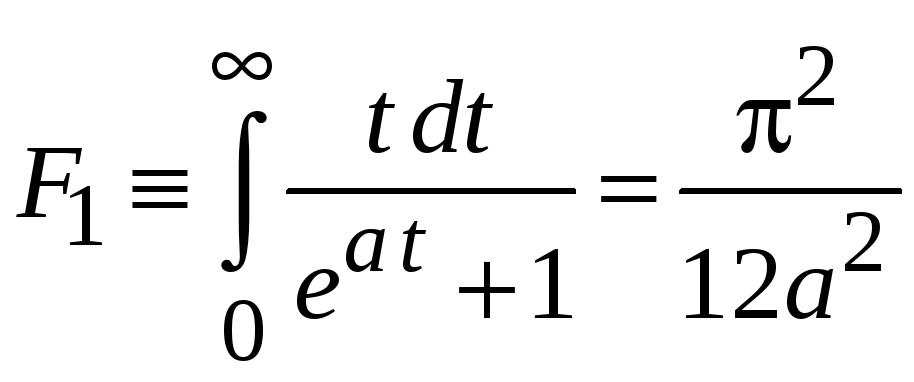 ,
,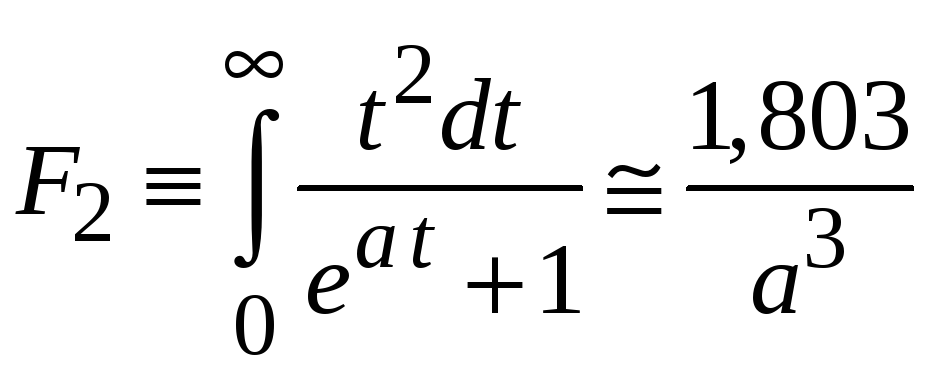 ,
,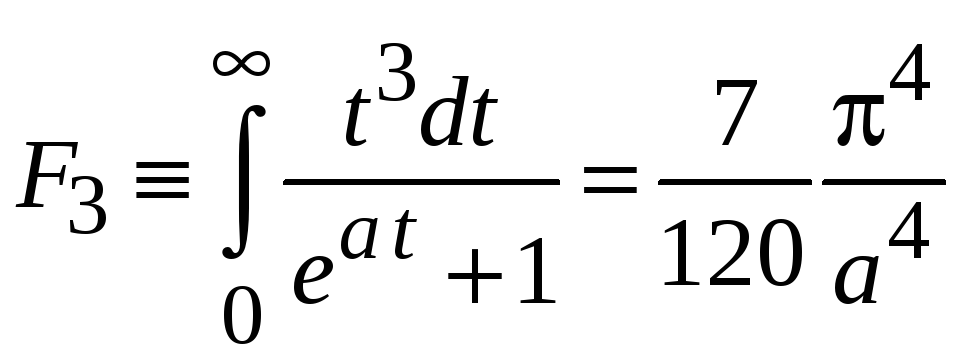 .
.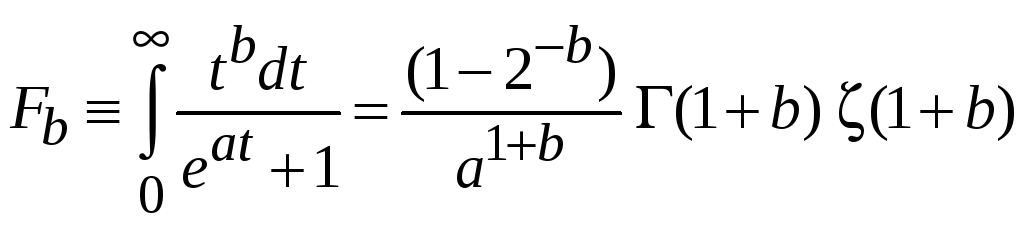 .
.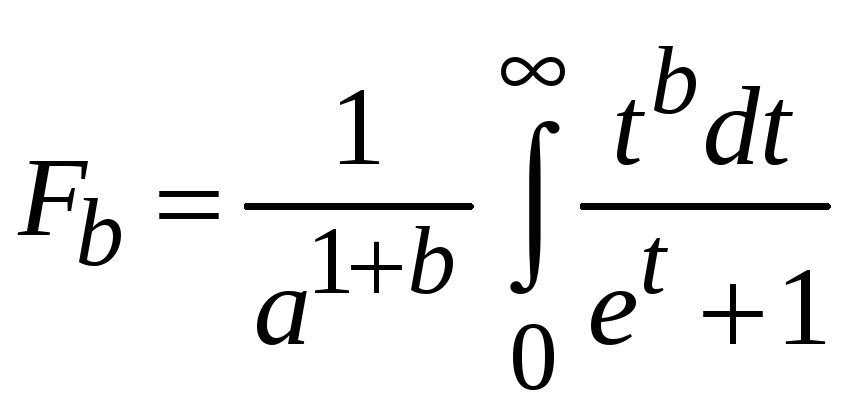 .
. ,
, .
. разлагаем в ряд Маклорена
разлагаем в ряд Маклорена
 ,
,
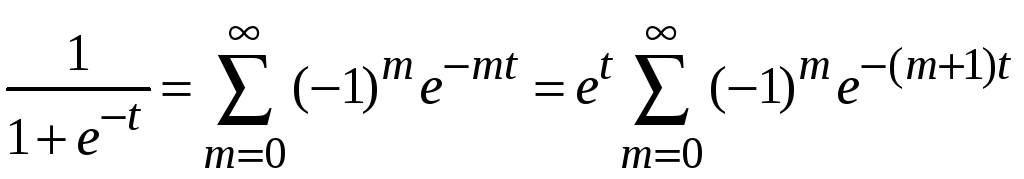 .
.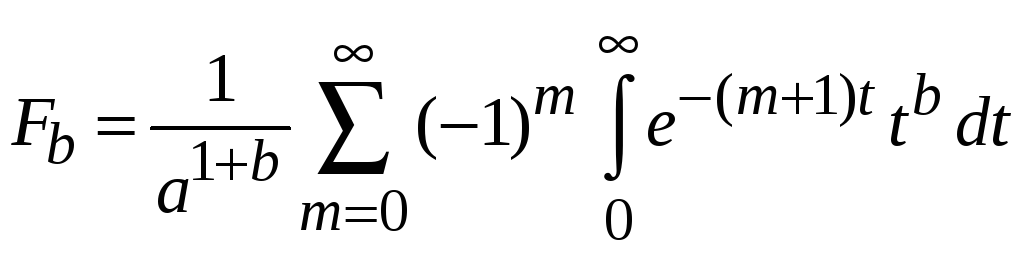 .
.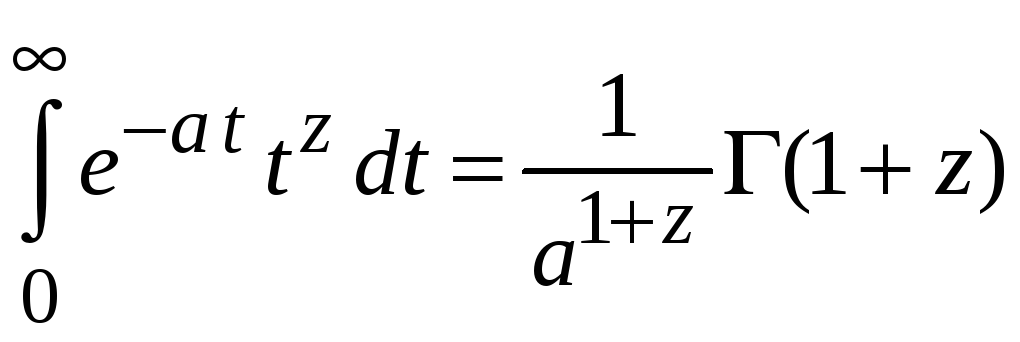
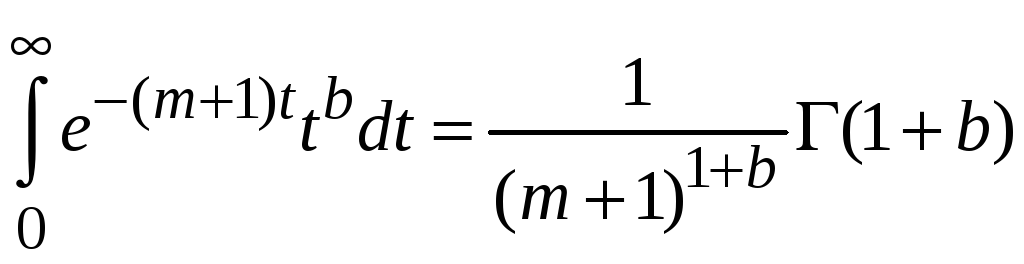 .
. .
.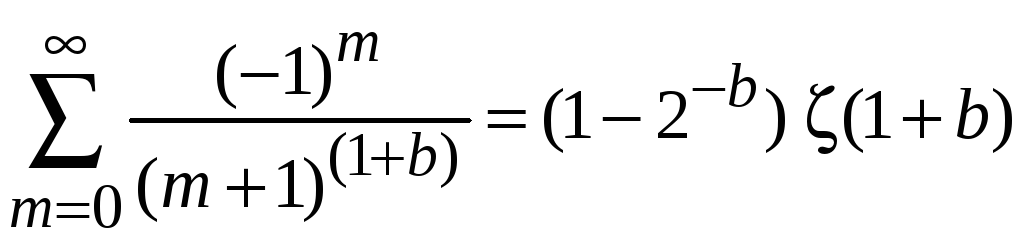 ,
(П.2.21)
,
(П.2.21)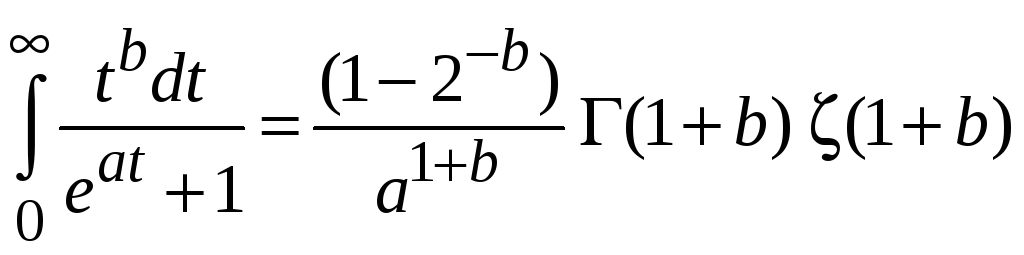 .
.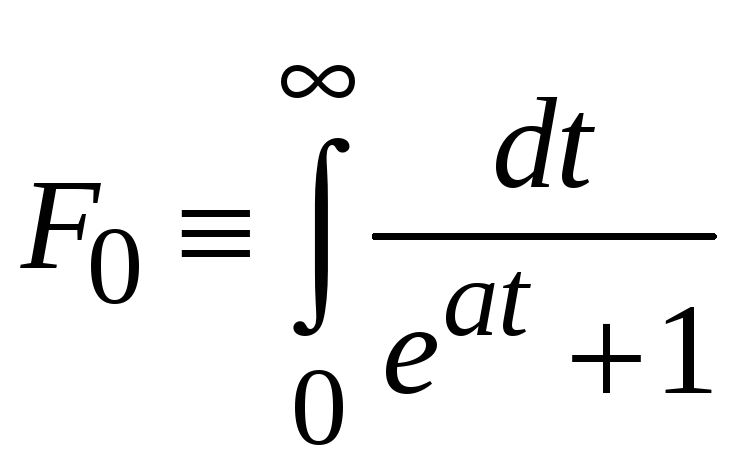
 ,
, ,
, ,
, .
(П.2.20)
.
(П.2.20)