Гамма-функция отрицательного полуцелого аргумента
Из (4.18)
при
,
используем
,
получаем
.
Учитываем (4.11)
,
находим
.
(4.17)
Частные
результаты при
,
и
:
,
,
.
Формула Стирлинга
Факториал с большим аргументом вычисляется по формуле
,
,
(4.23)
которую получил шотландский математик Стирлинг в 1730 г. Из (4.23) находим
.
(4.23а)
Джеймс Стирлинг (1692–1770)
Для доказательства (4.23) используем (4.7)
.
Интеграл вычисляем по формуле Лапласа.
Асимптотическая формула Лапласа
В
пределе
выполняется приближенная формула
,
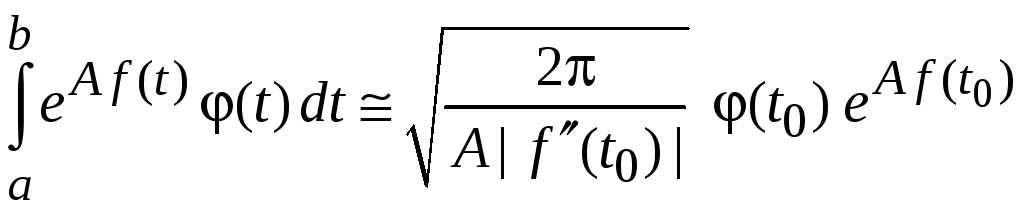(4.24)
где
– положение максимума
;
;
– гладкая функция. Формулу получил
французский астроном, математик и физик
Лаплас.
Пьер Лаплас (1749–1827)
Доказательство
Если
,
то
,
где
– основание неперовых логарифмов,
сильно изменяется даже при малой вариации
.
Поэтому главный вклад в интеграл
вносит
область t
около максимума
,
находящегося в точке
,
и можно заменить
.
Учитываем условия максимума
,
,
разлагаем
в ряд Тейлора около точки
,
и оставляем первые три слагаемые
.
Если
положение
максимума
находится далеко от концов области
интегрирования
,
то они не вносят заметного вклада в
интеграл, поэтому можно считать
,
.
В результате
,
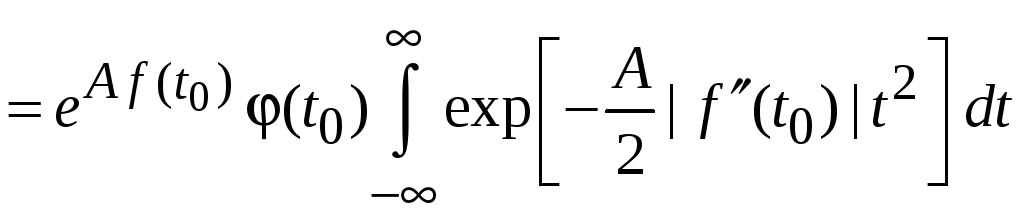где заменен
аргумент
.
Используем интеграл Пуассона (4.9а)
,
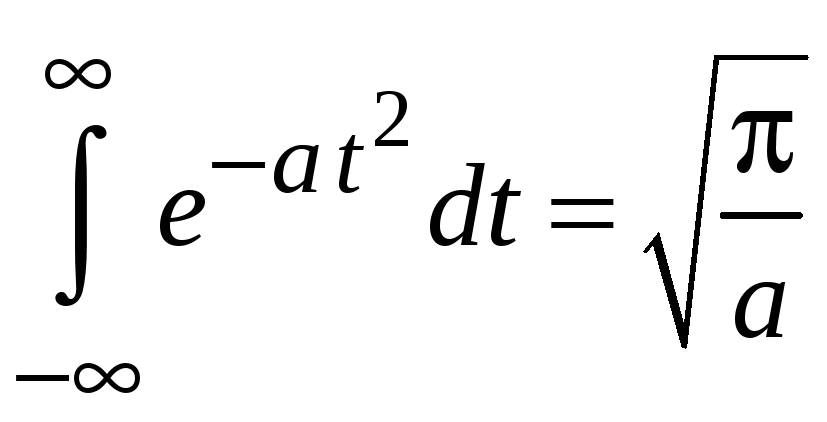где
,
и получаем формулу Лапласа (4.24)
.
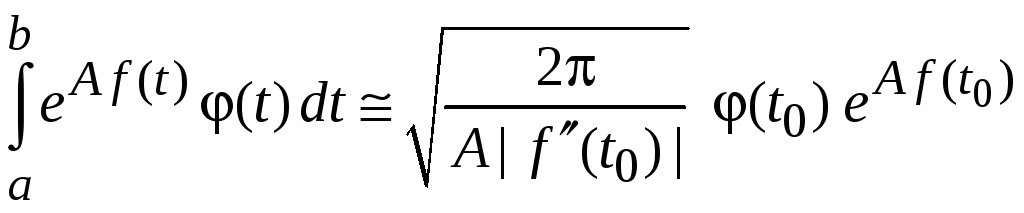Доказательство формулы Стирлинга
.
(4.23)
Используем
,
где учтено
,
,
тогда
.
Интеграл
сравниваем с формулой Лапласа (4.24)
,
,
тогда
,
,
,
,
получаем
,
(4.24а)
где
.
Находим
положение максимума
из уравнения
,
где
,
тогда
,
,
,
,
,
.
Из (4.24а) получаем формулу Стирлинга
.
Учет большего числа членов разложения в ряд Тейлора дает поправки
.
(4.26)
Пример 1
Доказать
,
.
(П.2.5)
Линейное
слагаемое
в показателе экспоненты (П.2.5) устраняем
заменой
,
тогда
.
Линейное слагаемое устраняем условием
,
находим
,
.
Интеграл получает вид
.
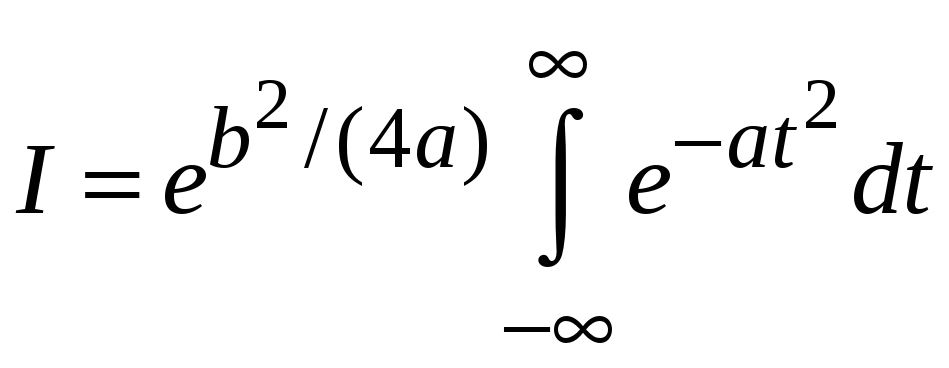Используем интеграл Пуассона (4.9а)
,
получаем (П.2.5).
Пример 2
Фурье-образ функции Гаусса
Выполняется
,
в явной форме
.
(П.2.6)
При
получаем
.
(П.2.6а)
Следовательно,
функция
Гаусса
инвариантна при преобразовании Фурье.
Доказательство (П.2.6)
Используем (П.2.5)
,
с параметрами
,
,
,
и получаем (П.2.6).
Пример 3
В квантовой статистической теории газа бозонов – частиц с целым спином (фотоны, фононы, атомы и др.), требуется вычислить интеграл
,
.
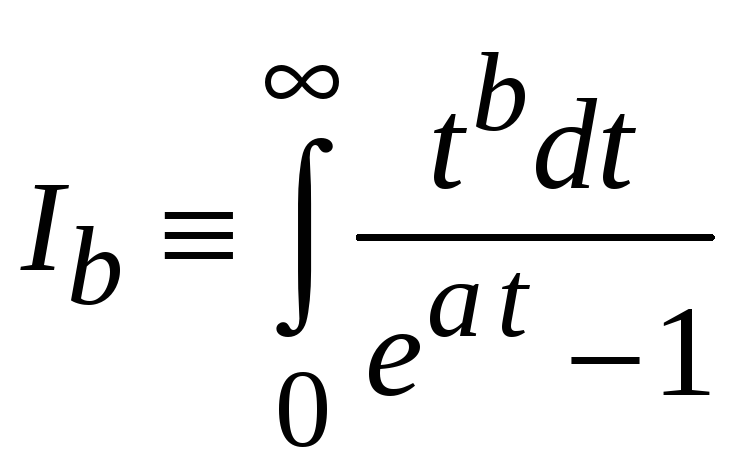Выполняется
,
(П.2.16)
где дзета-функция
(П.2.17)
введена Леонардом Эйлером. Частные значения:
,
,
,
,
,
.
(П.2.18)
Результат
рассматривается на практическом занятии
путем разложения функции
в ряд Фурье на интервале (–1,1). Из (П.2.16)
и (П.2.18) получаем
,
,
.
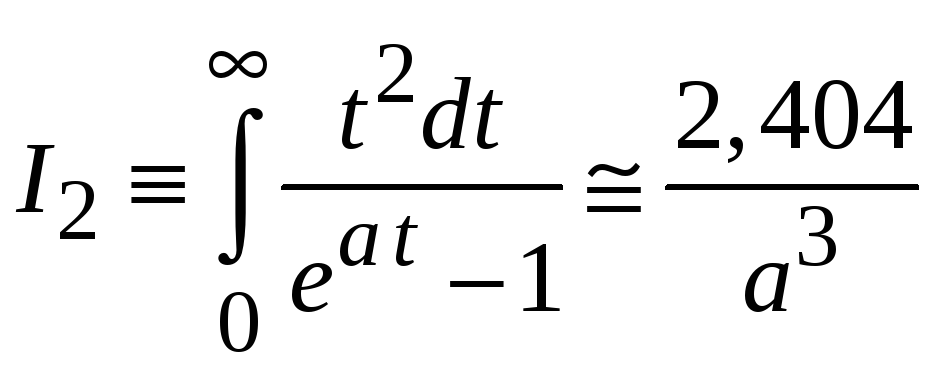Доказательство (П.2.16)
Интеграл
упрощаем
заменой
,
получаем
.
Преобразуем интеграл к виду гамма-функции
.
С учетом
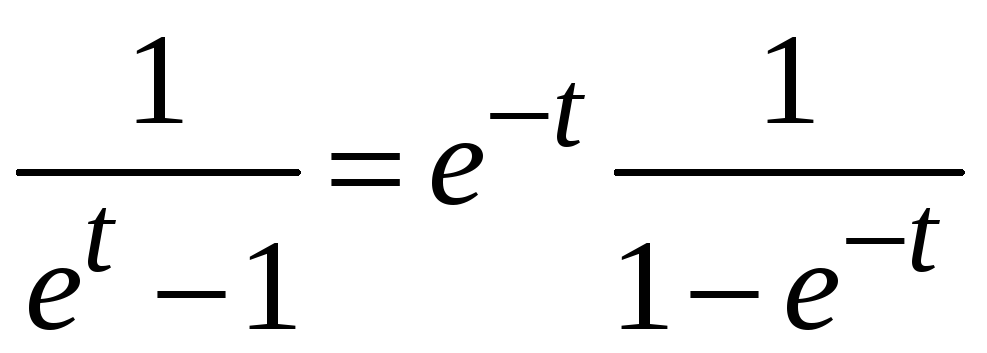
получаем
.
Функцию
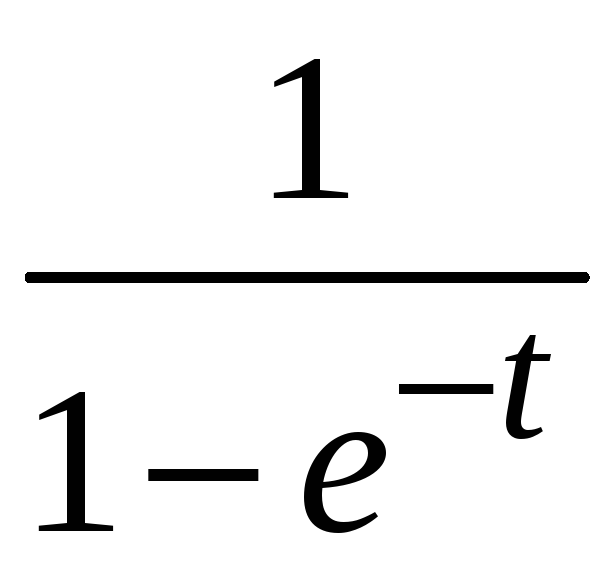разлагаем в ряд Маклорена
.
При
находим
.
Подстановка в интеграл дает
.
Используем (4.8)
при
,
,
получаем
.
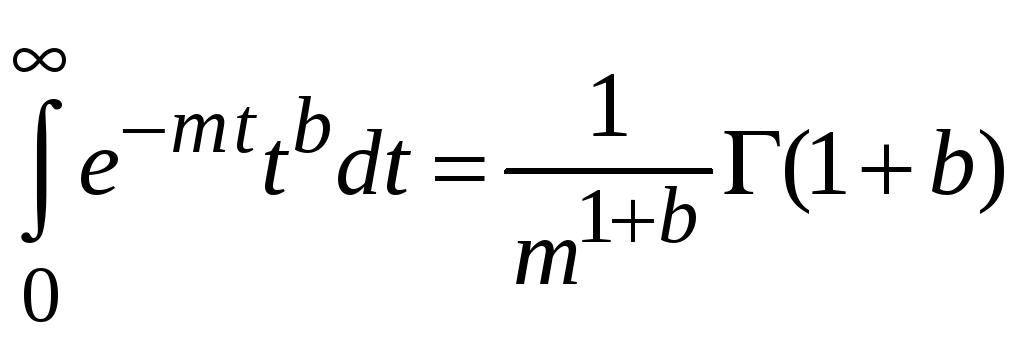В результате
.
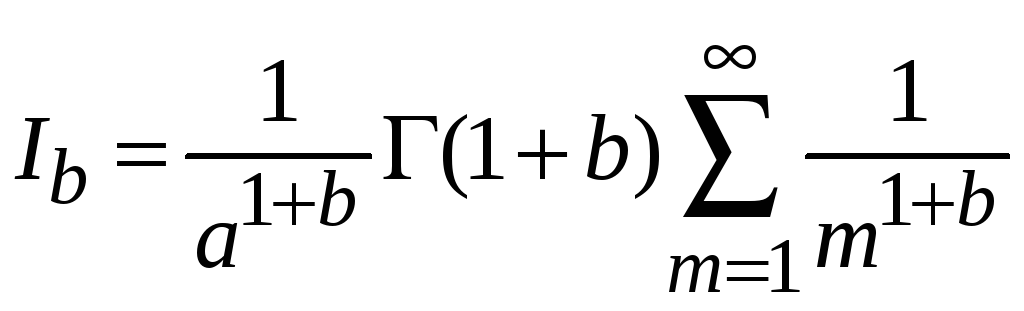С учетом
,
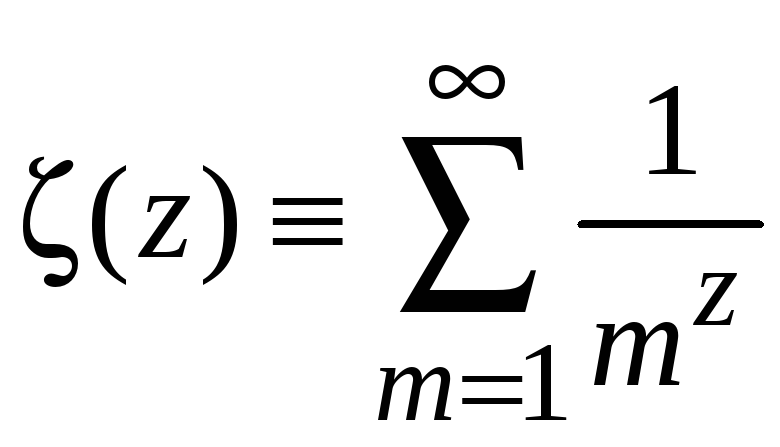доказано равенство (П.2.16)
.