
- •Сферическая функция
- •Момент импульса частицы
- •Повышающий и понижающий операторы
- •Уравнение для СферическОй функциИ
- •Разделение переменных
- •Значение
- •Пространственное квантование момента импульса
- •Сферическая функция
- •Инверсия координат
- •Рекуррентные соотношения
- •Разложение по сферическим функциям
Сферическая функция
![]() ,
,
![]() ;
;
![]() ;
;![]() ;
;![]()
1.
Описывает
угловую зависимость состояния объекта
в сферических координатах ![]() .
.
2. Описывает вращательное движение в теории излучения и рассеяния волн и частиц, в теории потенциала.
3. Определяется как собственная функция оператора момента импульса и оператора Лапласа.
4. Число l связано с модулем момента импульса.
5.
Число m
связано с проекцией момента импульса
на ось z.
Проекция вектора не может быть больше
его модуля, поэтому
![]() ,
для проекции возможны положительные и
отрицательные значения.
,
для проекции возможны положительные и
отрицательные значения.
6.
Набор
![]() образует полный ортонормированный
базис функций на единичной сфере.
образует полный ортонормированный
базис функций на единичной сфере.
Для получения уравнения сферической функции и ее свойств используется момент импульса.
Момент импульса частицы
В классической механике частица с импульсом p, вращающаяся вокруг точки О по окружности радиусом r, имеет момент импульса
![]() ,
,
где
![]() – мгновенныйрадиус-вектор
частицы. Направление L
перпендикулярно
– мгновенныйрадиус-вектор
частицы. Направление L
перпендикулярно
![]() и
и
![]() ,
и определяетсяправилом
правого винта.
,
и определяетсяправилом
правого винта.

В декартовых координатах
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Формулы переходят друг в друга при циклической перестановке
![]() .
.
В квантовой механике величины заменяются операторами
![]() ,
,
![]() ,
,
где
набла
![]() –оператор
градиента.
Получаем
–оператор
градиента.
Получаем
![]() .
.
Оператор градиента
В декартовых координатах
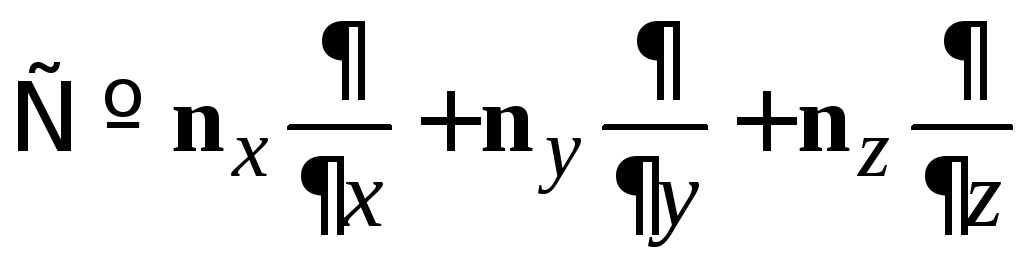 ,
(7.1)
,
(7.1)
где
![]() – орты декартовых координат. Действие
оператора градиента на функцию
– орты декартовых координат. Действие
оператора градиента на функцию![]() дает вектор
дает вектор
![]() .
.
Вектора
показывает направление наибольшего
возрастания функции. Модуль вектора
равен быстроте увеличения функции при
смещении точки
![]() вдоль вектора.
вдоль вектора.
Операторы момента импульса
![]()
В декартовых координатах получаем 4 оператора
 ,
,
 ,
,
 ,
,
![]() .
(7.2)
.
(7.2)
Формулы переходят друг в друга при циклической перестановке
![]() .
.
Предполагается, что правее любого оператора находится функция, на которую действует оператор.
Сферические координаты

![]() ,
,
![]() ,
,
![]() .
(7.3)
.
(7.3)
Орты декартовых и сферических координат

Оператор градиента в сферических координатах
 ,
(П.8.1)
,
(П.8.1)
где
![]() – орты сферических координат.
– орты сферических координат.
Операторы момента импульса
 ,
(7.4)
,
(7.4)
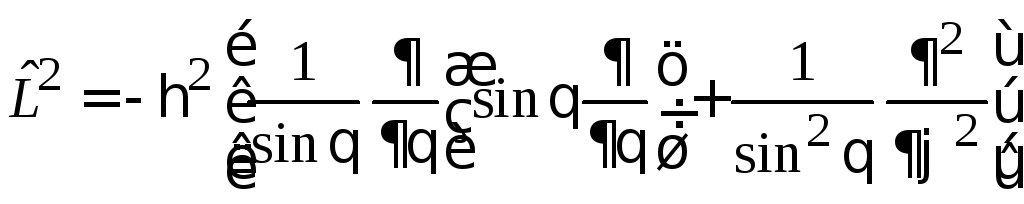 .
(7.5)
.
(7.5)
Оператор Лапласа
Оператор Лапласа определяет кинетическую энергию частицы. В декартовых и сферических координатах имеет вид
 ,
(7.6)
,
(7.6)
Радиальная часть оператора Лапласа
 (7.7)
(7.7)
определяет кинетическую энергию радиального движения.
Угловая часть оператора Лапласа

определяет энергию вращательного движения. Это слагаемое создает центробежную силу отталкивания от оси вращения, поэтому относится к потенциальной энергии. Этим объясняется знак минус.
Перестановочное соотношение операторов (коммутатор)
Коммутатор определяется в виде
![]() .
.
Предполагается, что правее каждого слагаемого находится функция, на которую действуют операторы:
![]() .
.
Выполняются
![]() ,
,
![]() .
.
Если
![]() ,
,
![]() ,
,
то
операторы
коммутируют,
их можно переставлять во взаимном
произведении, например:
![]() .
В общем случае необходимо следить за
порядком следования операторов.
.
В общем случае необходимо следить за
порядком следования операторов.
Физический
смысл коммутатора.
Если операторы коммутируют
![]() ,
то соответствующие им физические
величины измеримы одновременно с
неограниченной точностью. Это объясняется
совместимостью физических приборов,
выполняющих измерение. Если операторы
не коммутируют
,
то соответствующие им физические
величины измеримы одновременно с
неограниченной точностью. Это объясняется
совместимостью физических приборов,
выполняющих измерение. Если операторы
не коммутируют![]() ,
то чем точнее измеряется одна величина,
тем больше неустранимая погрешность
другой величины. Погрешности связанысоотношением
неопределенностей.
Соответствующие физические приборы,
выполняющие измерения, взаимно не
совместимы.
,
то чем точнее измеряется одна величина,
тем больше неустранимая погрешность
другой величины. Погрешности связанысоотношением
неопределенностей.
Соответствующие физические приборы,
выполняющие измерения, взаимно не
совместимы.
Для операторов момента импульса выполняются перестановочные соотношения
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
(7.8)
.
(7.8)
Следовательно,
определенные значения одновременно
имеют квадрат модуля момента импульса
![]() и одна из его проекций, например,
и одна из его проекций, например,![]() .
При этом остальные проекции становятся
неопределенными.
.
При этом остальные проекции становятся
неопределенными.
