Преобразование Ганкеля

Преобразование Ганкеля является разложением радиальной функции по ортонормированному базису функций Бесселя с непрерывным спектром. Преобразование прямое и обратное порядкаm связывают коэффициент Фурье исходной функции с коэффициентом Фурье ее образа.

С учетом (8.94) определяем

, (8.95)

, (8.96)

где

r и k – взаимно сопряженные переменные, – безразмерная,;

–радиальное распределение с угловой зависимостью для составляющей исходной функции;

–радиальное распределение с угловой зависимостью для составляющей функции образа.

Преобразования (8.95) и (8.96) взаимно симметричные – они переходят друг в друга при замене и.

Интегральная теорема

Действия прямого (8.95) и обратного (8.96) преобразований Ганкеля восстанавливают исходную функцию

,

. (8.97)

Доказательство:

В (8.97) меняем порядок интегрирований

,

где использована ортонормированность функций Бесселя (8.48)

.

Теорема о парах функций

Если для функции образом являетсясогласно(8.95)

,

то для функции образом является

. (8.97а)

Доказательство:

В обратном преобразовании (8.96)

заменяем и получаем (8.97а).

Масштабное преобразование аргумента

Выполняется

. (8.98)

Доказательство:

Используем

,

где сделана замена и проведено сравнение с (8.95)

.

Теорема Парсеваля

Теорема Парсеваля утверждает, что скалярное произведение функций равно скалярному произведению их образов.

Марк-Антуан Парсеваль (1755–1836) – французский математик. Исследовал дифференциальные уравнения и функции комплексного переменного. Доказал «теорему Парсеваля» в 1799 г. Теорема выполняется для любого унитарного (сохраняющего скалярное произведение) преобразования – Фурье, Бесселя, Ганкеля и других. Портрет Парсеваля не найден.

Для преобразования Ганкеля скалярное произведение функций равно скалярному произведению их образов

, . (8.99)

Доказательство:

В интеграл (8.99) подставляем (8.96)

,

,

и меняем порядок интегрирований

.

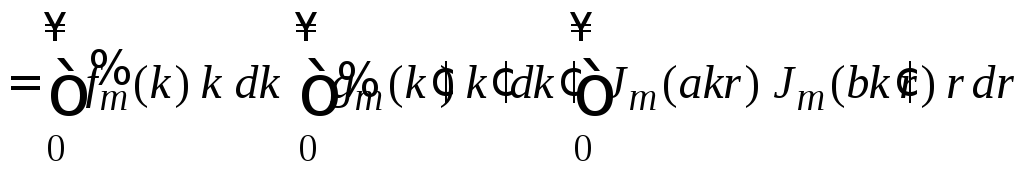Используем ортонормированность функций Бесселя (8.48)

в виде

,

тогда с учетом фильтрующего свойства дельта-функции

,

где сделана замена .

Преобразование Фурье–Бесселя

Прямое преобразование Фурье–Бесселя выражает исходную функцию через коэффициенты Фурье ее образа . Обратное преобразование выражает функцию образачерез коэффициенты Фурье исходной функции .

Исходная функция и ее образ связаны преобразованием Фурье (8.91) – (8.92)

,

.

Функцию разлагаем по углу φ в ряд Фурье по базисусогласно (8.93)

.

Коэффициенты , зависящие от радиуса, выражаем через преобразование Ганкеля (8.96)

.

В результате исходная функция в полярных координатах выражается через коэффициентыобраза Ганкеля

. (8.100а)

Функцию образа разлагаем по углу α в ряд Фурье по базисусогласно (8.94) и (8.95)

,

.

В результате Фурье-образ в полярных координатах выражается через коэффициенты исходной функции

. (8.100б)

Формулы (8.100а) и (8.100б) являются разложениями функции и ее Фурье-образа, выраженных в полярных координатах, по функциям с определенной проекцией орбитального момента.

Коэффициенты ис одинаковым индексомm связаны между собой преобразованием Ганкеля

, .