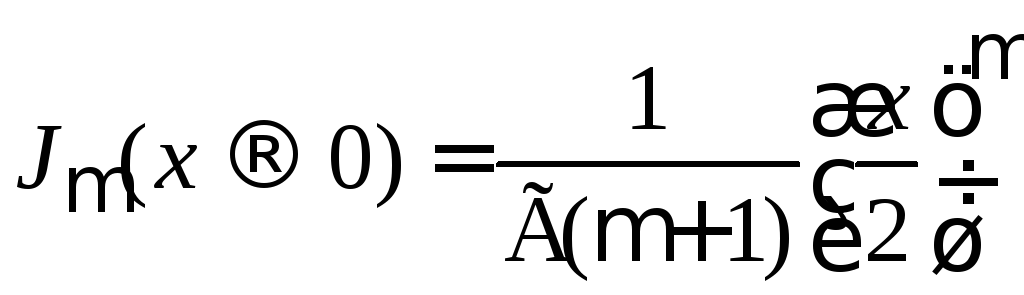ФункциИ Бесселя полуцелого порядка

Функции Бесселя целочисленного порядка не сводятся к элементарным функциям. Функции полуцелого порядка выражаются через тригонометрические функции.

Вид функций

1. Используем представление (8.9) в виде ряда

.

При получаем

.

С учетом

,

находим

.

Сумма является разложением , в результате

. (8.53)

2. Из (8.42)

при  = –1/2 с учетом (8.53)

,

получаем

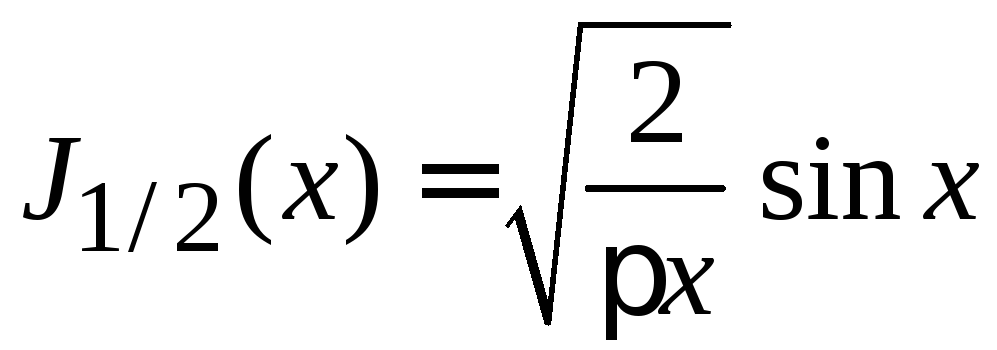. (8.54а)

3. Из (8.37)

при  = 1/2 находим

,

откуда

. (8.54б)

4. Из (8.43)

,

при

,

с учетом (8.53)

,

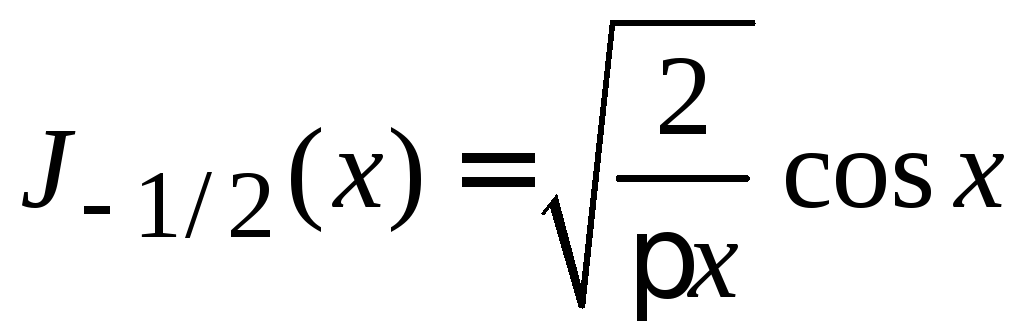находим

. (8.55)

5. Из (8.41)

,

при

,

с учетом (8.54а)

получаем

. (8.56)

Нули функций

Функция зануляется

в точках , где k – порядковый номер нуля. Числовые расчеты для первых двух нулей дают

x_0,1 = 3,0, x_0,2 = 6,2;

x_1,1 = 4,4, x_1,2 = 7,7;

x_2,1 = 5,7, x_2,2 = 9,0.

Графики функций

,

Сферическая функция Бесселя

Определяем

, (8.57)

Функция описывает в сферических координатах радиальную зависимость плоской волны с волновым числом k и с орбитальным моментом l. Ранее показано, что коэффициент Фурье n-ого порядка по угловой переменной плоской гармонической волны является функцией Бесселя .

Множество при образует ортонормированный базис с непрерывным спектром .

Радиальная зависимость волны

Плоская волна в сферических координатах удовлетворяет уравнению Гельмгольца

,

где оператор Лапласа (7.6)

,

–оператор квадрата момента импульса; – волновое число.

В уравнении разделены производные по радиусу r и углам (, ), находящимся в . Ищем решение в виде произведения независимых функций

,

где – сферическая функция, удовлетворяющая (7.20):

.

В уравнение Гельмгольца

,

подставляем решение

.

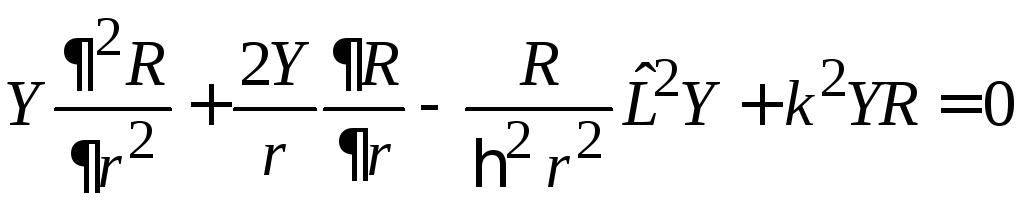Учитываем ,делим слагаемые на Y, и для радиальной функции получаем уравнение

.

Замена дает

.

Сравниваем с уравнением Ломмеля

,

находим

, , ,.

Общее решение (8.4)

,

получает вид

,

где учтено (8.57)

.

Физическое решение должно быть конечным при . С учетом (8.11)

Устраняем расходимость условием , получаем

.

Следовательно, радиальная зависимость плоской волны с волновым числом k и с орбитальным моментом l описывается сферической функцией Бесселя.

Уравнение для

Определение сферической функции Бесселя (8.57)

,

сравниваем с решение уравнения Ломмеля (8.3)

,

находим

, , ,.

Уравнение Ломмеля

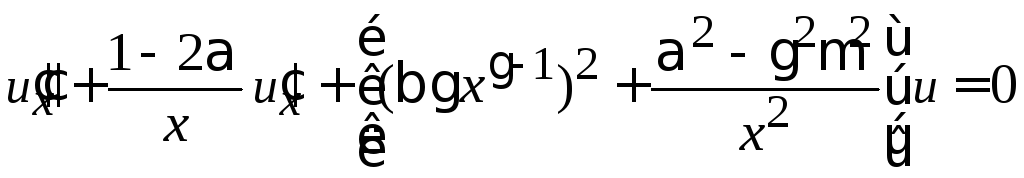
дает уравнение для сферической функции Бесселя

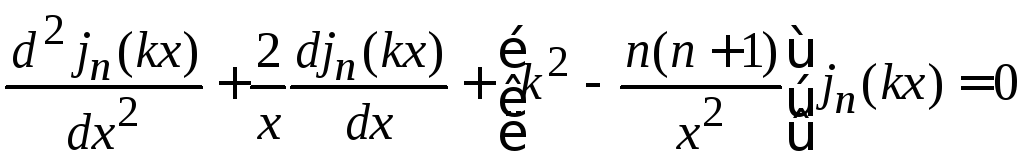. (8.58)

Явный вид функции

Используем (8.57)

.

В (8.55)

заменяем , и находим

.

В результате сферическая функция Бесселя

. (8.59)

Свойство четности

Из (8.59) получаем

. (8.61)

Функции низших порядков

Из (8.59) получаем

,

,

. (8.62)

Предел x  

Используем (8.12а)

находим

. (8.63)

Из (8.57)

получаем

,

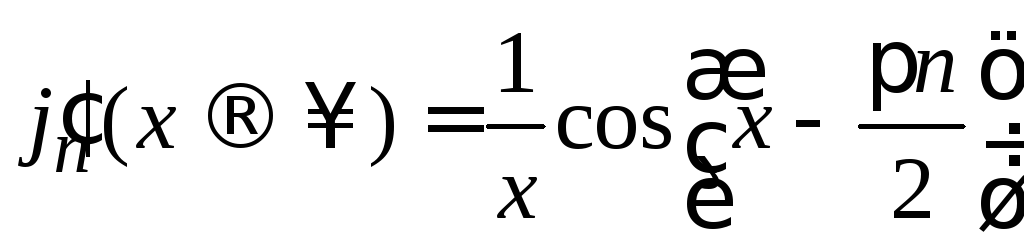. (8.64)

На большом расстоянии от начала координат сферическая функция Бесселя меняется периодически с амплитудой, убывающей обратно расстоянию.

Предел x  0

Используем (8.11)

,

при

.

Подставляем в (8.57)

,

получаем

, (8.65)

откуда

,

,

,

. (8.65а)

На малом расстоянии от начала координат сферическая функция Бесселя не нулевого порядка n стремится к нулю как расстояние в степени n.

Условия ортонормированности

1. Используем (8.48)

, ,

при

.

Из (8.57)

выражаем

,

.

Получаем условие ортонормированности при

. (8.66)

2. При не нулевой вклад в (8.66) с учетомдает только. Используя, находим

, . (8.67)

Этот результат не следует из (8.66).

Доказательство (8.67)

Умножаем (8.67) на и интегрируем по интервалу. В левой стороне меняем порядок интегрирований и прииспользуем (8.66)

.

Правая сторона дает тот же результат

,

где учтено

.

Получение тождества доказывает (8.67).

3. Из (8.67) и (8.62)

, ,

получаем

. (8.68)