Объем и площадь n-мерной сферы

На основании размерности для объема n-мерной сферы радиусом r, объема шарового слоя толщиной dr и площади сферы получаем

, ,.

Найдем постоянную , вычислив сходящийся интеграл

по всему пространству в декартовых и сферических координатах.

В декартовых координатах

,

,

тогда

,

где использован интеграл Пуассона

.

В сферических координатах

,

тогда

,

где использовано

.

Гамма-функция вычисляется по формулам

Г(n + 1) = n!, ,

Г(z + 1) = z Г(z),

,

, ,,

при .

Сравниваем выражения в декартовых и сферических координатах

, ,

находим

.

В результате объем n-мерного шара, шарового слоя и площадь сферы

, (П.2.1)

. (П.2.2)

. (П.2.3)

В частности при с учетомполучаем

, ,.

Эллипсоид с полуосями удовлетворяет уравнению

.

Сравниваем с уравнением сферы

,

обобщаем (П.2.1)

,

находим объем n-мерного эллипсоида

. (П.2.1а)

Фазовая траектория

С течением времени система изменяет свое микросостояние за счет движения частиц, и точка X перемещается по фазовой траектории согласно уравнениям Гамильтона (2.1)

, .

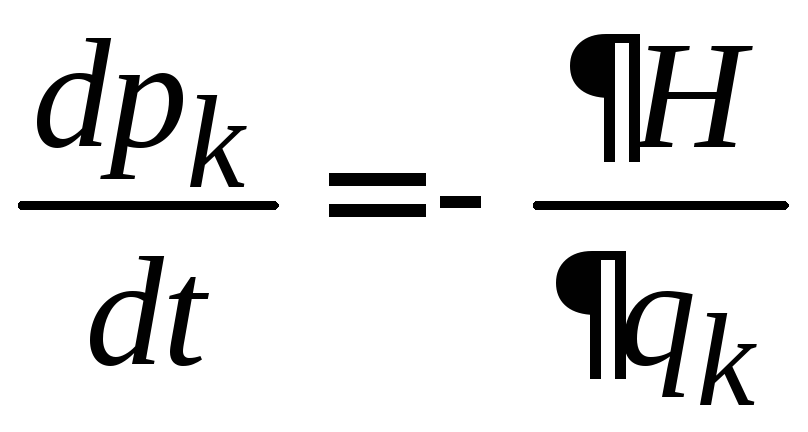Фазовый ансамбль

Макросостояние системы характеризуется макроскопическими и термодинамическими характеристиками, в частности: числом частиц N, температурой T, объемом V, давлением P, внутренней энергией U, свободной энергией F, энтропией S. Одному макросостоянию соответствует множество различных микросостояний, меняющих свое положение в фазовом пространстве с течением времени. Все они находятся в пределах некоторой области фазового пространства, границы которой зависят от макрохарактеристик. Фазовые траектории микросостояний не выходят за пределы указанной области. По истечении некоторого времени микросостояние возвращается в свое начальное положение со сколь угодно высокой точностью. Фазовый ансамбль есть множество микросостояний с одинаковыми макрохарактеристиками, т. е. относящихся к одному макросостоянию.

Функция распределения микросостояний фазового ансамбля

Точка X фазового пространства описывает микросостояние системы. В бесконечно малом объеме

около точки X вероятность реализации микросостояния равна . Вероятность реализации в единичном объеме около точкиX называется функцией распределения, или плотностью вероятности

. (2.3)

Вероятность нахождения системы в интервале

(2.3а)

удовлетворяет условию нормировки

, (2.4)

где интегрирование ведется по всему фазовому пространству.

Плотность вероятности пропорциональначислу реализованных микросостояний в единице объема фазового пространства, т. е. плотности микросостояний. Установим свойства , используя теорему Лиувилля.

Теорема Лиувилля

Равновесный газ описывается стационарным, то есть не зависящим от времени, гамильтонианом и постоянными термодинамическими параметрами. Макросостояние реализуется фазовым ансамблем микросостояний. Это множество точек с течением времени движется по фазовому пространству. Закон их перемещения описывает теорема Лиувилля – при движении точек фазового ансамбля плотность микросостояний вдоль траектории постоянна и зависит от гамильтониана