Свободная энергия и статистический интеграл

Из (2.15) и (2.16) получаем соотношение между свободной энергией и статистическим интегралом , тогда

. (2.25)

Термодинамическая величина F выражена через статистическую величину Z, которая вычисляется интегрированием гамильтониана системы по фазовому пространству

.

Соотношение (2.18) подставляем в (2.25) и получаем

, (2.25а)

где при использована формула Стирлинга. Подстановка (2.24в) дает

, (2.25б)

где – энергетическая плотность спектра состояний частицы.

Внутренняя энергия и статистический интеграл

Внутренняя энергия является средним по фазовому ансамблю значением полной энергии системы

.

Используем (2.16) и (2.17)

, ,

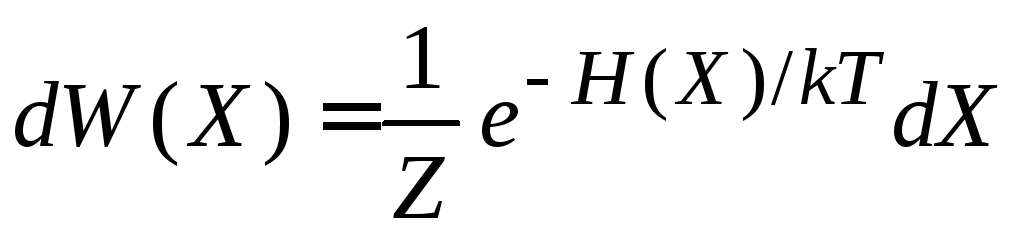находим

,

где использовано

, .

Учитываем

,

и получаем выражение внутренней энергии через статистический интеграл

. (2.26)

Уравнение Гиббса–Гельмгольца

Соотношение между внутренней и свободной энергиями называется в термодинамике уравнением Гиббса–Гельмгольца. Для его получения исключим статистический интеграл из (2.25) и (2.26).

Выражение (2.25)

записываем в виде

и подставляем в (2.26). Получаем известное в термодинамике уравнение Гиббса–Гельмгольца

. (2.27)

Следовательно, F – свободная энергия. Из (2.27) находим теплоемкость

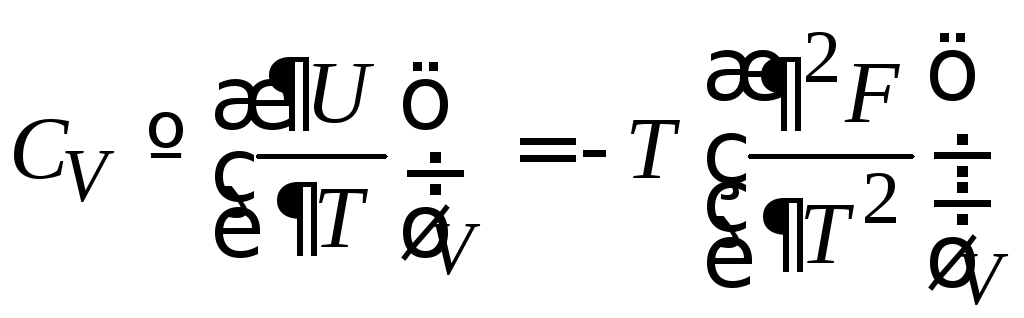. (2.27а)

Выразим F через U. В первом равенстве (2.27) перегруппировываем сомножители и получаем

.

Интегрируем и выражаем свободную энергию через внутреннюю энергию

, (2.28)

где учтено , как следует из (2.28).

Термодинамические потенциалы

Потенциалом называется функция состояния системы, не зависящая от пути перехода системы в это состояние.

Свойства потенциала:

1. Для потенциальной функции выполняется

;

2. При интеграл равен нулю – изменение потенциала при переходе системы из некоторого состояния по замкнутому пути в исходное состояние равно нулю;

3. Потенциал является полным дифференциалом своих аргументов.

Термодинамические потенциалы являются функциями макроскопических характеристик состояния системы: T, V, P, S, N, и отличаются друг от друга набором аргументов.

Внутренняя энергия – термодинамический потенциал, зависящий от объема, числа частиц и энтропии:

.

Полный дифференциал

. (2.29)

Из первого начала термодинамики

,

и из определений энтропии и работы для равновесного, обратимого процесса при

,

находим

. (2.29а)

Сравнение с (2.29) дает

, . (2.29б)

Свободная энергия – термодинамический потенциал, зависящий от объема, числа частиц и температуры:

,

. (2.30а)

Энтропия – термодинамический потенциал, зависящий от внутренней энергии, объема и числа частиц:

,

. (2.30б)

Физический смысл свободной энергии

В термодинамике свободная энергия определяется в виде

. (2.31)

Берем дифференциал

. (2.31а)

Для равновесного, обратимого процесса используем определение энтропии и первое начало термодинамики

, .

Сравниваем с (2.31а) при , и получаем

.

Свободная энергия является частью внутренней энергии, которая при изотермическом процессе переходит в работу.

Из (2.31) следует – свободная энергия равна внутренней энергии при.