6. Капля жидкости в насыщенном паре

В насыщенном паре образовалась капля жидкости с коэффициентом поверхностного натяжения  радиусом R. Получим условия увеличения и уменьшения размера капли. Аналогичная задача возникает для квантовой точки, образующейся в насыщенном растворе.

При образовании капли происходит переход N частиц пара в жидкость. Для этого химический потенциал пара должен превышать химический потенциал жидкости. При изотермическом и изохорическом образовании капли система равновесная при минимуме свободной энергии. Из (2.67) с учетом энергии поверхностного натяжения жидкостиполучаем

,

где S – площадь поверхности жидкости.

При образовании капли увеличивается площадь поверхности жидкости на , гдеR – радиус капли. Изменение свободной энергии

, (П.7.15)

где

–число частиц жидкости в капле; v – объем частицы.

В равновесной системе размер капли не меняется. Равновесие соответствует экстремуму свободной энергии

.

Используем

,

получаем равновесный радиус капли

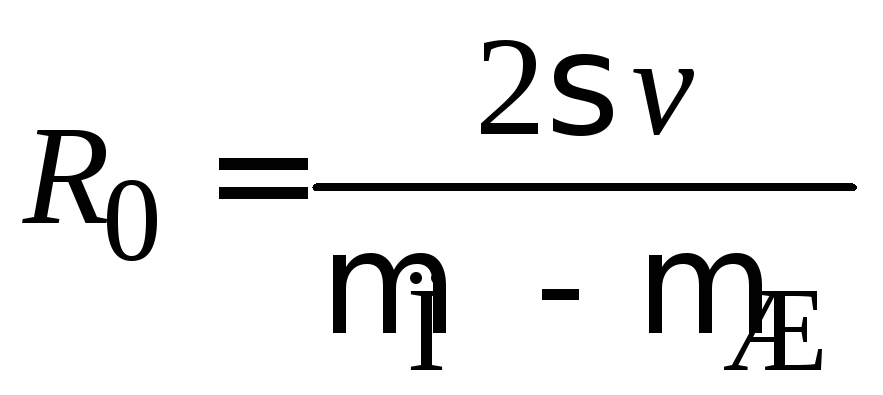. (П.7.16)

С учетом

выполняется

.

Следовательно, свободная энергия максимальна. Устойчивое равновесие соответствует минимуму свободной энергии, поэтому состояние капли неустойчиво: при капля увеличивается; прикапля испаряется. Как изменится состояние капли, если она образуется вокруг иона?

7. Заряженная капля в насыщенном паре

Ион радиусом имеет зарядq, его окружает пар c химическим потенциалом . Вокруг иона образовалась капля жидкости радиусомR c химическим потенциалом , причем. Найдем изменение свободной энергии при образовании капли.

Используем обозначения и результаты примера 4. Дополнительно учитываем энергию электрического поля капли

,

где

–плотность электрической энергии;

–объем шарового слоя радиусом r толщиной dr;

 – диэлектрическая проницаемость жидкости;

–напряженность поля внутри капли при ;

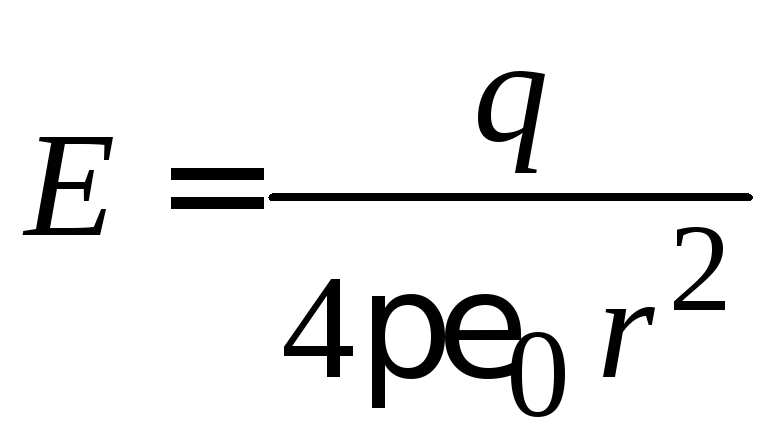–напряженность поля вне капли.

К вкладу без поля (П.7.15)

Добавляем энергию поля внутри и вне капли

=.

При достаточно большом заряде q и малом размере иона главную роль играет третье слагаемое. Оно отрицательное и уменьшается с увеличением радиуса каплиR. При уменьшении свободной энергии возрастает устойчивость системы. В результате заряженная капля увеличивается даже в ненасыщенном паре.

Если капля получает заряд за счет эмиссии электронов, то, как показал Джон У. Рэлей в 1882 г., при достаточно малом размере R₀ ~ 50 мкм, называемом пределом Рэлея, капля становится неустойчивой из-за преобладания сил электростатического отталкивания над поверхностным натяжением. Капля вытягивается, из ее концов выбрасывается заряд, переносимый струями жидкости.

Условия применимости классической статистической физики

На рубеже XIX–XX вв. делались попытки применить классическую статистическую физику для описания электромагнитного теплового излучения в полости, электронного газа в металле, тепловых свойств кристалла. Оказалось, что в этих областях следствия теории противоречат опыту. Рассмотрим примеры.

Теплоемкость твердых тел. Металл состоит из кристаллической решетки ионов, потерявших свои валентные электроны, и электронов, ставших свободными. Для моля одновалентного металла количество ионов равно количеству свободных электронов и равно числу Авогадро . Теплоемкость металла

содержит вклады электронного газа и ионов решетки. Свободный электрон имеет 3 степени свободы и по теореме о распределении энергии по степеням свободы его средняя энергия. Внутренняя энергия моля и молярная теплоемкость электронного газа

, ,

где универсальная газовая постоянная . Ион решетки имеет 3 колебательные степени свободы, на каждую приходится тепловая энергия, тогда средняя энергия иона, внутренняя энергия моля и молярная теплоемкость кристаллической решетки

, ,.

Для молярной теплоемкости металла получаем

,

для диэлектрика, не имеющего свободных электронов:

.

Эксперименты при нормальной и более высокой температурах подтверждают закон Дюлонга и Пти (П.4.7)

как для металлов, так и для диэлектриков. Следовательно, электронный газ не дает вклада в теплоемкость металла. При температуре, существенно меньшей нормальной, эксперимент обнаруживает зависимость теплоемкости от температуры – для диэлектриков ; для металлов. Для объяснения этих результатов необходимо учитывать квантовые свойства микрочастиц.

Магнетизм системы зарядов. Согласно теореме Бора – ван Лёвен, рассмотренной в Примере 3.10, система зарядов не проявляет магнитных свойств, что противоречит свойствам магнетизма ряда металлов.

Ограничения на параметры системы. Требуется очертить рамки, в пределах которых применима классическая физика и несущественны квантовые свойства, главными из которых являются:

1. Интерференция и дифракция частиц, приводящие к квантованию энергии системы и к дискретности фазового пространства. Волновые свойства частицы описываются длиной волны де Бройля , и условием квантования Бора–Зоммерфельдана траектории ;

2. Вырождение состояний по энергии;

3. Тождественность микрочастиц и принцип запрета Паули для фермионов.

Ограничим области параметров системы, для которых применима классическая статистическая физика.

Высокие температуры. Для частицы в кубическом ящике со стороной L условие квантования Бора–Зоммерфельда допускает дискретные значения импульса . Энергия частицы квантуется. Дискретность спектра несущественна, если расстояние между уровнями гораздо меньше тепловой энергии

. (2.190)

Для и массы электрона получаем, что равно тепловой энергиипри температуре.Классическая теория выполняется для частиц, находящихся в макроскопическом объеме при относительно высокой температуре, если масса частицы не слишком мала.

Малая концентрация частиц. Длина волны де Бройля несущественна при большом расстоянии r между частицами

.

Для наиболее вероятной скорости частицы газа (2.124) , импульси длина волны де Бройля

.

Среднее расстояние междуN частицами газа выражаем через объем сосуда V и концентрация , находим,

.

Получаем условие

. (2.191)

Классическая теория идеального газа выполняется при достаточно малой концентрации, высокой температуре и не слишком малой массе частицы. Как следует из (2.162), в области применимости классической теории химический потенциал газа отрицательный.

Для гелия при нормальных условиях

, ,

, ,,

выполняется и классическая физика применима.

Для электронов металла при нормальной температуре

, ,.

Классическая физика не применима для электронного газа в металле.

Для полупроводников длина волны де Бройля электрона в нанометрах дана в таблице.

	Ge	Si	GaAs	InSb
	12	15,4	58	134
	6	7,7	29	67

В узкозонных полупроводниках с шириной запрещенной зоны , напримерInSb и InAs, концентрация электронов проводимости велика, , условие классического описаниянарушается.

Большой объем фазового пространства, занимаемый узлом кристаллической решетки, по сравнению с постоянной Планка

. (2.192)

Флуктуации импульса и координаты выражаем через параметры системы. По теореме о распределении энергии по степеням свободы средняя кинетическая энергия одномерного движения узла кристаллической решетки

,

тогда . С учетомтепловая флуктуация проекции импульса

.

Для потенциальной энергии упругих колебаний с частотой ω аналогично находим

, .

Чем прочнее кристалл, тем больше частота – для меди , для алмаза. Тепловая флуктуация координаты узла с учетомравна

.

В результате

.

Условие (2.192) получает вид

. (2.193)

Чем прочнее кристалл и ниже температура, тем меньше согласие с классической теорией. Классическая физика не применима для прочных кристаллов при низкой температуре.

Для систем, нарушающих хотя бы одно из полученных условий, необходимо использовать квантовую статистическую физику.