
Собакин Е.Л. Цифровая схемотехника (УП)
.pdf
') # ) ". "
'.
|
|
|
2.4 |
|
|
|
|
-& ! " |
-& |
||
" &- |
155 |
531 |
K555 |
& * |
4 ! " & |
4 ! " & |
4 ! " & |
|
74 |
74S |
74LS |
155 |
10 |
8 |
40 |
155,% # |
30 |
24 |
60 |
531 |
12 |
10 |
50 |
531,% # |
37 |
30 |
150 |
555 |
5 |
4 |
20 |
555,% # |
15 |
12 |
60 |
' )$ 3 , # ' & *, |
|||
! $ ') %: |
|
||
|
3 = 3 (1+0,21·f ), |
(2.27) |
|
& f − $# ' )*!, , # -
" ; 3 − $# # # 60
! )$. (2.27) ! $ $# # + - # ) , 3 -
$ ' # ' )$ - !. ( & % " (2.27) ) +
' 5)*!. - ! $. 1)*! - # ) ! $.
& & & * ( $ ) ! # & , . . -$' " & #! # U"(t) = f(t) $
.
( ", ') -
& , ! " " &-
*, ! ') " " &-
".
" $ (&.1) ' -
$' %, % " & $ (&.0) ! #
$ ( .2.12). - # «"» + !
- , -* -* ,
#) " *, ( .1.24), ! - ! , -
& # " # " " -
! ") #, ' ! -
" & #! #.
101
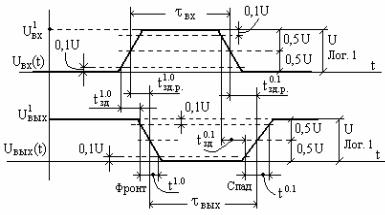
$ " + «' "» $ " -
, # + #$#, "
+ # # # # # #. * ' " -
! & $ . (# * %
$ .) " $" ' #-
&$' %, $ τ τ" #' # 0,5U, & U − #!, # $ &.1 ( .2.12).
|
' |
- |
||
|
') |
" |
- |
|
|
" |
" |
*- |
|
|
: |
|
|
|
|
∙ |
t1.0 . − # - |
||
|
! # |
|||
|
& ' |
|||
|
60 ( #- |
|||
|
# &.1 # |
|||
|
&.0 , , - |
|||
|
1→0); |
|
||
|
∙ |
t0.1 . − # - |
||
.2.12. ' " - |
||||
" & * ( |
! |
- |
||
# & " '-
& & * ( 0→1);
∙t1.0 . − # ! ' # * (! % "- & $ );
∙t0.1 . − # ! " ' # * (! "- & $ );
∙t1.0 − # ' # 60( $ $ % " & $ );
∙t0.1 − # " ' # * ( $ $ " & -
$ ).
" ", ! # t1.0 . t 0.1 . ,
#' # # 0,9U 0,1U #! #, # &
&.1, , # & &.0. - .2.12 $ &.0 - # #!, '. , " " " #' #
# " 60 ( & # $" # *-
&. - , # ( 6 155
" # # " # #' #
+25°-, +$ & ( ≤ 15', *%% #
" =10.
4 " " " ' # t1.0 . t0.1 . .
& .2.12, ! " ' * (2 --5)
!+ 2 $. ! # & '. # 60 & # t1.0 . 15 t0.1 . 22…29 . ( #
102
* " ' ') # t1.0 . 7 t0.1 . 13 . . # 2# #' #, ! &,
" " " &
" ! ") #.
# + ' 60 " -
$# + # ! t . . # &, - # # %
t . . = (t1.0 . + t0.1 . ) / 2. |
(2.28) |
( & % (2.28) # ( 6 & # &-
# #
F& = 1 / t . . =2·109/ (t1.0 . + t0.1 . ) = 2·109/ (15+25) = 50) !.
, & # ' $
+ &, " &
" * (. * # # - ! " " & " + " . - # " .
1" & ! -
# & &
« » & " (" ") . 5 -
$ " $ , " ' # & * ", ') " " $ & &
') ".
" t1.0 . t0.1 . # ! ", , - # # (. + & %$"
& %$ " ! -
# & "$ ", # " #
"$ $. !. 4 % (2.28) $
'' ! # ! & & & * # ! ". ( # !, ! # "-
#, " # %
|
k |
|
T . |
= t . c . .i |
(2.29) |
|
, |
|
|
i=1 |
|
& t . . . i − ## ! # # i-& & & *-
, k − & *, ')
& #.
( $, # ( 6. " " *-
(" 7 ) ' ! ") #, & #
' $ # #! ', * !
# & * " $ $., "-
$. ( . .2.3).
103
2.6.1. . ($( , %! ! ! $%& '
, ! %$" '- # , * # # #, " # &-
# & ! " . 0 , -
$" " " ,6 % " 6 " ( ! ,
, & . &, # # #
$" #! # # " ' # #
).
) ($( , %! ! ! ! 2# #-
' # ! , ! ( . .2.5.2).
$ , $" # #
. # & #, #') #$ " - # $" %$"
, . 0 # & # # #
'):
1.- # $ $ " & % #
(8,) * %$" , ') 8,( 5( # ! # $" . 8, ! " -
$ $ ) ') *-
.
2." # * "
! " !$ # !
, . 0 # " ' #
# " & & * (") -
" ( ), * # # &
". - , DD1.3, $ -
' % " ( ) # " -
«1» & * «3» . -
# $ $ " (D) (,
#' # $ % " ", , D1.3. # # & "
$ $ " DA…
3.- # " " 8, & * ( ) ! " "$ " ( -
). # "$ 8, ! " "
# ' # #! # ) & - ' ( ) #. 0 # # # -
$ (
!) " .
# # . - , « " " 14 -
D1, D4…D15, '$ . # +5(,…» . .
104
4. # 8, , . -
$ ", , 15&, 2200', 0,5* -
. $. ! " $" # *
# ! $, %$
% $ . 3 & # ! " % "
(, & $" " # # &
" # #, # "$ " . - ! $ 8, ! $ " (+).
( # % #'
" , -
! & . # * # $ -
! %$ % $-
.
5.5 $# ! $-
. %$" " ( ), ! "
" ' «'» $' , -
$ , 8, # &$
) ". * # # "
# . $" " & & -
" ' # $', $" " ' # " -
(8,). # $ ( "$) 8,
$. , # $. & .
* " " " ! " "$ ) . # " #
*, ') , $ # " , -
& .
" ! -
$" $ -
" .
6.$" " ( %$" ") % #' #
! " 8,( 5( % # .-
! ' # " #. " - " 8, * , ! # $, ! " "$ " ! " & " 8,( [9].
7.$" " &$ -
$" " ' # " 8,, +
$" " ( " ' #. 0 # %-
", & " (, .
9.$" " ( !) -
. # # # ! -
$ , 3, 4, 5 #) ,
! " !$:
105
∙# * &
" & ;
∙# # − " " #
') #! *, # " -
# ( ) #, $# )$
. - , # * & " , &$" - & * . .;
∙# ' # $" ( -
) & *. 0 # " * ' -
# * &;
∙". ' "
# " # , +-
#! & " -
.
( #, " #, #' & -
" (!, .) "-
$ & $ "
#.
" " $ , -
') $" (. ,
$" * * " #- ) & #.
! " !$ #
$ &$" , " -
* * & , ,
, %-" # -"
*. * & . , # -
& # &$" ..
&, " ' # $' -
%$ &. 0 !
# ( &.
3. !$% & ' & , %
,-* ! "&,
( $ " $' & -
$' " &.
0 # $.
, $ " " & !$ + -
$ # " # " & *-
, * (( ( 1 () ' # %$ !-$' $ " # $- ".
106
', − * %$" , - #') $ ' & ' % ',
$ «"» & % % ' $. &
& ( 10). +, -
!, & , %!,
! . ' $ * ,
& , %,-* ! "&,! 6 ,0 % -
" ( $ ) ,-* & '.
$" & # &$ -
# #: ("- $"), -
,
(4 4), ! (6)
" &.
,-* ! " # ( )
# ' # , ! " "- ' . " #' # «"»
" $ ' ' − *
! "% ) & ' ( ' & & '. "-
#' # ", ! +$ " #- # (+ $'). $ - ' # $ − * ! "% ) &-
' " "& , ' & & '.
( ## " ", ! !$, -
& -
. ) *
# # # !$ # ( )
, " ! " % - & # " % & # ! " -
. ' $ * !$ + ) '
. &, "
' * " #- " % + #. # # &- %$". , # , & "$ " -
. # $. " . *
* . - , $ -
$ & ' # " "
. #, # # !$ # % *-
, +$ * # . * . " "$
# $ " " -
.
107
3.1. # , % " " %-" !&, (, %
# , %' " " (. %) − # (&
$), ') # k , " " «"», N =2k ". ' & & # ! "$ $ "-
, (« ») & # # &-
" ) . 5 " "
$ # " , # #, - & " ! $, # k-# , -
! ') ' & " , # ' -
#. # * & " ' " *%%-
" & " *%% # " 2i, & i{0, 1, 2,...(k-1)}, '. , k " ' «(-
" !» " " . 5 k =3, * " " & - (-
" & N=23=8 ". " " & "$ # " -
", * & & # " & & # # − " " # -
&.0, " # &.1.
$" " " ' $" ",
" " «. #/ », & "
" . ' ) ' # " & - & #. # « » " ! #-
$# & & #. 8 " &-
# 8, " . , .3.1, .3.1, " -
" & % # " $& + &
# . + .3.1, ' " "
& 3-& # # " " - " ') , .3.1, 8, $ -
155 3. 8, .3.1, : " " & & # # # &.1 ! #$#, ') (
E) & &.0. " -
# & ,-* - &,. - , .3.1, " "
", . . " # & &.0. * & ! #$#, ') & " &.0,
" 51 52 " & " # " " " (2'). , «&» &, " &
$ 8,. 5 # " "
& &.1, ! # #
" & -,% ,-.1.
$. # ) # DC-3
# # «" $& #», DC-4 − «" -
+ & #».
108
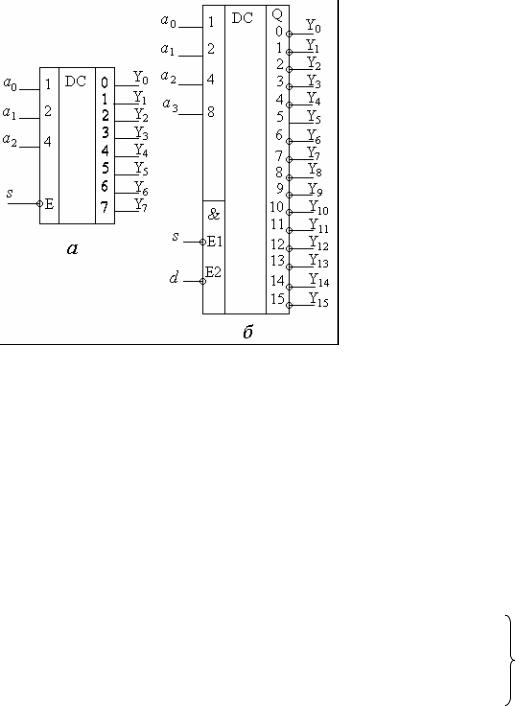
# & & # " (DC) + ')
& " %: { i}− ! " ",
" & " -
. i $ $ 2
« » & . ,
# 0, 1, 2, 3 . . (k-1) '$ ; {Yj} − ! " " %, " " " & -
. ,, j - & # 0 (#) N- 1. , 0 −
|
|
|
& |
||||
|
. & |
# |
|
|
|||
|
20=1, " 1 2 − |
||||||
|
! ' |
|
|
||||
|
# " |
& |
|
|
|||
|
" |
|
|
||||
|
' |
|
|
||||
|
21=2 22 = 4 . & |
||||||
|
# DC-3 - |
||||||
|
" & ! %- |
||||||
|
$ " |
||||||
|
< 2 1 0> $ - |
||||||
|
- |
||||||
|
2' '. * |
||||||
.3.1. " & % # |
+ ! - |
||||||
, ## # - |
|||||||
" $& # ( ), - |
|||||||
" 155 3 ( ) |
", |
- |
|||||
: ( -
) .0, "
, ( ) .1, − .
- , <110> ( a2 a1 a0 ) , # -
" 2=1, 1=1 0=0, 6- " ,
110 # .$: 110(2) = 6(10). , -
, " # % # DC-3 Y6=1 (&.0) &-
') 5 ( .3.1, ). ( + &
.3.1, ! $ ') & (") %-
:
Y0 |
= s( a2 a1a0 ); Y1 = s( a2 a1a0 ); Y2 = s( a2 a1a0 ) ; |
|
Y3 |
= s( a2 a1a0 ); Y4 = s( a2 a1a0 ) ; Y5 = s( a2 a1a0 ); |
(3.1) |
Y6 |
= s( a2 a1a0 );Y7 = s( a2 a1a0 ) . |
|
109

(3.1): Y0, Y1, ...Y7 − " " %; s − #, - ') # & ') ; " ! # & " ,
$ ( , ! 6 /, ! %70$' + ".
& ", ! ! # # #-
# " ! " % "
«! % ». s = 0, s =1 ! %-
Yi ( , !& ! 6 & & &, % &$' + -&! .
( % (3.1) ! $ )+ ( )
%:
Y |
~ ~ ~ |
) |
, |
(3.2) |
|||
= s( a |
2 |
a a |
0 |
||||
i |
|
1 |
i |
|
|
||
& i {0, 1, 2,...7} − " & $& #
! # # " " & % + &; ! 2' (a~2 a~1a~0 )i $ !-
" % 3- &. ($ , "
3-& # # " " ! $ «&-
» & % 3- & * $-
$ # # ' " & # . 3 &, % 155 3 ( .3.1, ) !
$ %
~ ~ ~ ~ |
i {0,1,2,....,14,15}. |
(3.3) |
Yi = (sd )(a3 a2 a1a0 )i , |
" " " ( !
$' " ! # 3.3), & & # (&.0) !
#$# .$ sd = 1, $ s=d=0. + i -
& " #$# < 3 2 1 0>i, )-
') " " . !-
{i} # # # " ! # " - & % ( ) #, . . #
!.
($ , " 4-& # ! $ $ #
# ' " & "$# .
, ) # " " ! (3.2) (3.3) " ",
& $, ( , % " " % )&0 &$,-( , %'
& «*» ( ), " ! $ ' " & . $# # #
# ') , ! " &
( ).
- ') . # %$" !-
, $ ! $ $
" & . - , # 155 3
110
