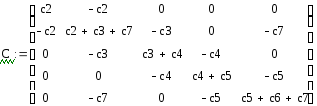3.2 Решение в Excel

Составим матрицу масс и матрицу жесткости пружины. Найдем обратные матрицы масс и жесткостей. Вычислим матрицу H1 как произведение матрицы масс на обратную матрицу жесткостей и матрицу H2 как произведение обратной матрицы масс на матрицу жесткостей. В итоге получаются значения максимальной и минимальной частоты колебаний, и соответствующие им собственные векторы:

	1,000		0,495
	-3,667		0,227
H1=	0,328	H2=	0,640
	-0,073		1,000
	0,917		0,221

3.3 Решение в Mathcad

Значения совпали с полученными раннее в Excel.

3.4 Решение в Fortran

Программа состоит из двух подпрограмм: головной и стандартной функции MINV, необходимой для вычисления обратных матриц.

Текст головной подпрограммы:

integer,parameter::n=5 real::mass(n,n), mass_1(n,n), jest(n,n), jest_1(n,n), h1(n,n), h2(n,n), x(n), y(n), m1=1., m2=0.5, m3=1.2, m4=2, m5=0.8 integer::ll(n), mm(n); c2=2; c3=0.8; c4=1.2; c5=0.9; c6=1.5; c7=1.; mass=0; mass(1,1)=m1; mass(2,2)=m2; mass(3,3)=m3; mass(4,4)=m4; mass(5,5)=m5; jest(1,:)=(/c2,-c2,0.,0.,0./) jest(2,:)=(/-c2, c2+c3+c7, -c3, 0., -c7/) jest(3,:)=(/0.,-c3,c3+c4,-c4,0./) jest(4,:)=(/0., 0., -c4, c4+c5, -c5/) jest(5,:)=(/0., -c7, 0., -c5, c5+c6+c7/) print*, 'M'; print*, mass; print*, 'C' print*, jest; jest_1=jest; call minv(jest_1, n, det, ll, mm) print*, 'C obr'; print*, jest_1 h1=matmul(mass, jest_1) print*, 'H1'; print*, H1; print*, 'y/x' x=1; do i=1,20; y=matmul(H1,x); print*, y/x; x=y; enddo mass_1=mass; call minv(mass_1, n, det, ll, mm) print*, 'M obr'; print*, mass_1 h2=matmul(mass_1, jest) print*, 'H2'; print*, h2 x=1; do i=1,20; y=matmul(H2,x); print*, y/x; x=y; enddo end

3.5 Вывод

Значения, полученные в трех программных продуктах совпадают друг с другом. Задача решена верно.

4.Определение собственных форм колебаний упругой балки

4.1 Постановка задачи

Требуется определить три первые формы колебаний упругой балки (рис. 4.1). Безразмерные параметры f, g, w, q приведены в таблице 4.1.

Исходные данные. Таблица 4.1

f	g	w	q
1	1	0	1

При решении задач на определение собственных форм колебаний упругих балок функцию прогиба удобно записывать через функции Крылова S(x), T(x), U(x), V(x), которые представляют собой линейные комбинации гиперболических и тригонометрических синусов и косинусов:

Рис. 4.1. Балка

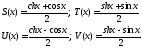(4.1)

Собственные формы Y(z), где z – безразмерная координата, колебаний консольной балки через функции Крылова определяются как:

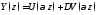(4.2)

Параметры иD зависят от граничных условий на правом конце балки. Собственные значения определяются из следующего характеристического уравнения:

(4.3)

Уравнение (4.3) имеет бесчисленное множество положительных корней . Для каждого значениякоэффициентD определяется из уравнения: (4.4)

Каждому значению иD соответствует своё значение Y(z).