
Лабораторная работа №2
Исследование линейных электрических цепей синусоидального тока
Цель работы: исследование соотношений для токов и напряжений в электрической цепи синусоидального тока при последовательном и параллельном соединении ёмкости и катушки индуктивности, а также изучение особых режимов работы таких цепей: резонанса напряжений и резонанса токов.
I. Основные теоретические сведения
I.I. Синусоидальные токи и напряжения
Наибольшее распространение в электротехнике получили синусоидальные ЭДС, токи и напряжения. Источниками синусоидальных ЭДС являются генераторы переменного тока, принцип действия которых основан на явлении электромагнитной индукции.
Синусоидальные ЭДС, токи, напряжения могут быть представлены выражениями
![]() ,
,
![]() ,
,
![]() ,
,
где
![]() ,
,![]() ,
,![]() - соответственно мгновенные значения
ЭДС, тока,
- соответственно мгновенные значения
ЭДС, тока,
напряжения;
![]() ,
,![]() ,
,![]() - соответствующие амплитудные значения
ЭДС, тока, напряжения;
- соответствующие амплитудные значения
ЭДС, тока, напряжения;
![]() -
угловая частота;
-
угловая частота;
![]() -
период синусоидальной функции;
-
период синусоидальной функции;
![]() -
частота;
-
частота;
(![]() ),
(
),
(![]() ),
(
),
(![]() )
- фазовые углы или фазы функций;
)
- фазовые углы или фазы функций;
![]() ,
,
![]() ,
,![]() - начальные фазы.
- начальные фазы.
Графики
синусоидально изменяющихся ЭДС, тока,
напряжения, имеющих одинаковый период
изменения, но различные начальные фазы
(![]() ,
,![]() ,
,![]() )
приведены на рис.1.
)
приведены на рис.1.
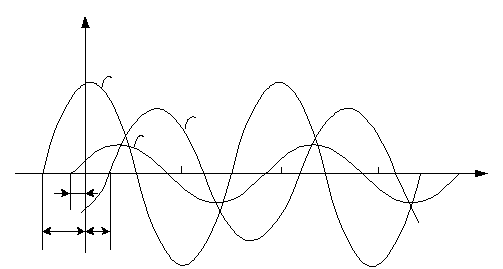
Рис.1
Наряду
с мгновенными и амплитудными величинами
используются понятия о среднем и
среднеквадратичном (действующем)
значениях переменного тока, напряжения,
ЭДС. Н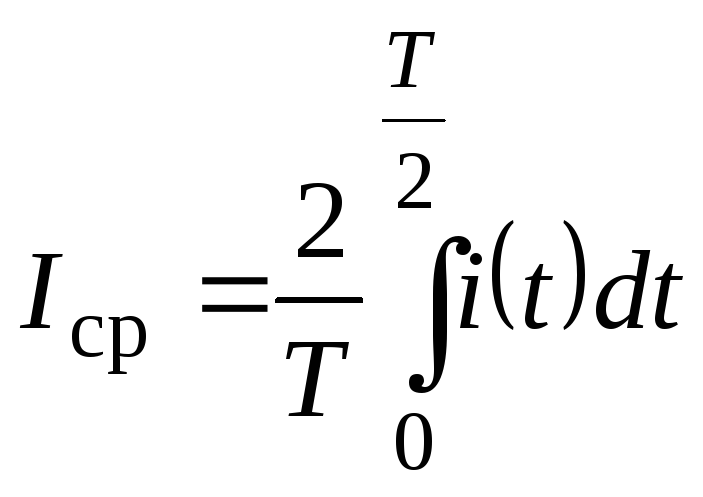 апример,
апример,
- среднее значение тока;
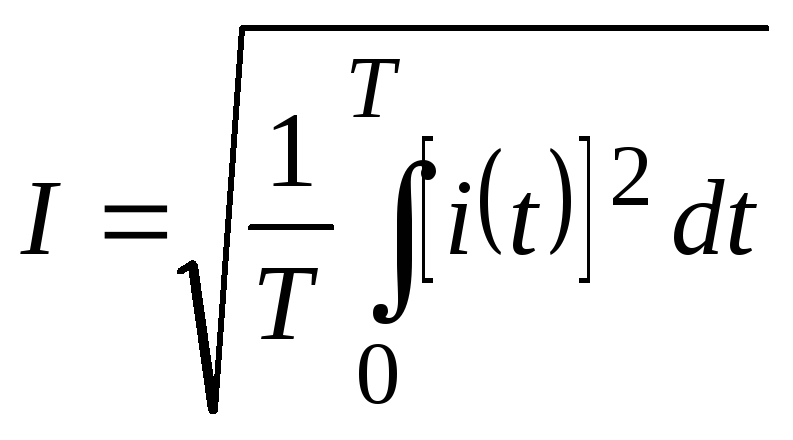
- действующее значение тока.
Для синусоидального тока
![]() ,
,![]() .
.
1.2. Векторные диаграммы
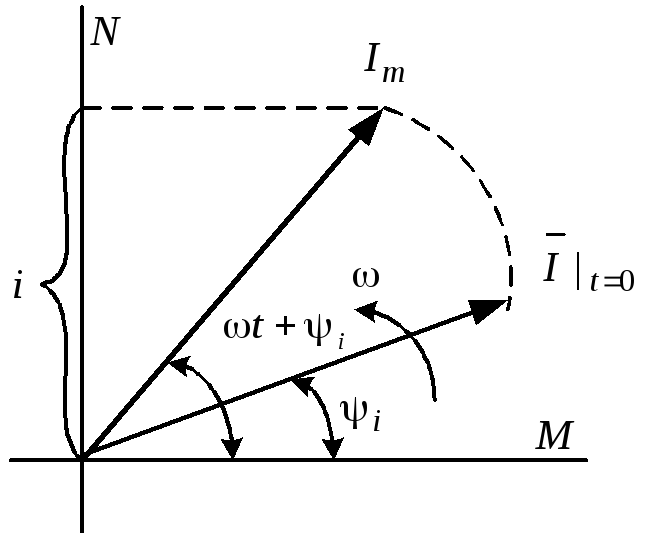
Синусоидально
изменяющиеся функции могут быть
изображены с помощью векторов
![]() ,
,![]() ,
,![]() ,
вращающихся с угловой скоростью
,
вращающихся с угловой скоростью![]() против
часовой стрелки. На рис.2 за начало
отсчёта углов выбрана ось ОМ. В начальный
момент времени вектор
против
часовой стрелки. На рис.2 за начало
отсчёта углов выбрана ось ОМ. В начальный
момент времени вектор![]() ,
изображающий ток
,
изображающий ток![]() ,
составляет с осью ОМ угол
,
составляет с осью ОМ угол![]() ;
через время
;
через время![]() -
угол
-
угол![]() .
Проекция
.
Проекция![]() на осьON
для этого момента времени равна
на осьON
для этого момента времени равна
![]() .
.
Аналогично изображаются и другие синусоидально изменяющиеся величины. Так как все векторы вращаются с одинаковой скоростью ω, то их взаимное расположение остаётся неизменным для любого момента времени.
 Совокупность
векторов,
изображающих
синусоидально
Совокупность
векторов,
изображающих
синусоидально
изменяющиеся
токи, напряжения, ЭДС некоторой
электрической цепи, называется векторной
диаграммой. Векторные диаграммы строятся
для момента времени
![]() .
.
Рис.2
Так как при рассмотрении векторных диаграмм существенным является только взаимное расположение векторов, то начальная фаза одного из них может быть принята равной нулю.
1.3. Активное сопротивление, индуктивность и емкость в
цепи переменного тока
Активное
сопротивление
(![]() ).
Для любого момента времени соотношение
между током и напряжением в активном
сопротивлении (рис.3,a)
определяются законом Ома:
).
Для любого момента времени соотношение
между током и напряжением в активном
сопротивлении (рис.3,a)
определяются законом Ома:
![]() .
.
При синусоидальном напряжении на зажимах сопротивления (начальная фаза напряжения принята равной нулю) ток в сопротивлении также синусоидален
![]()
и совпадает по фазе с напряжением.
Соответственно для амплитудных и действующих значений токов
и напряжений имеем:
![]() ,
,
![]() .
.
На рис.3,б представлена векторная диаграмма напряжения и тока.
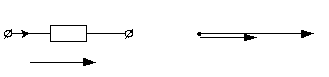
а б
Рис.3
Индуктивность
(![]() ).
Синусоидальный
ток
).
Синусоидальный
ток
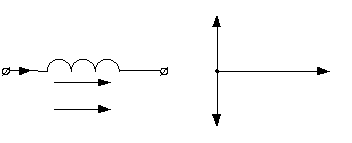
![]() индуктивности (рис.4,а) вызывает ЭДС
самоиндукции
индуктивности (рис.4,а) вызывает ЭДС
самоиндукции
![]()
,
![]()
уравновешивающую приложенное напряжение
![]()
.
Анализ
этих выражений показывает, что напряжение
опережает по фазе ток на угол
![]() ,
ЭДС отстаёт от тока на угол
,
ЭДС отстаёт от тока на угол![]() ,
кроме того,
,
кроме того,![]() ,
,
![]() .
.
Величина
![]() ,
имеющая размерность сопротивления,
называется индуктивным сопротивлением.
,
имеющая размерность сопротивления,
называется индуктивным сопротивлением.
Векторная диаграмма напряжения, ЭДС и тока показана на рис.4,б.
а б
Рис.4
Емкость
![]() .
Синусоидальное напряжение
вызывает
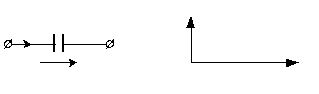
в емкости (рис.5,а) ток
.
Синусоидальное напряжение
вызывает
в емкости (рис.5,а) ток
![]()
,
опережающий
приложенное напряжение по фазе на угол
![]() .
.
При
этом
![]() ,
,
![]() .
.
Величина
![]() ,
имеющая размерность сопротивления,
называется емкостным сопротивлением.Векторная диаграмма
напряжения и тока показана на рис.5.
,
имеющая размерность сопротивления,
называется емкостным сопротивлением.Векторная диаграмма
напряжения и тока показана на рис.5.
а б
Рис.5
1.4. Эквивалентные схемы приемников электроэнергии
В лаборатории в качестве приемников электрической энергии используются конденсаторы и катушка индуктивности. Исследования проводятся при частоте
50
Гц. При такой частоте конденсатор
достаточно точно характеризуется только
величиной его емкости
![]() .
Катушка индуктивности обладает
существенным электрическим сопротивлением
и может быть представлена эквивалентной
схемой, состоящей из последовательно
включенных индуктивности
.
Катушка индуктивности обладает
существенным электрическим сопротивлением
и может быть представлена эквивалентной
схемой, состоящей из последовательно
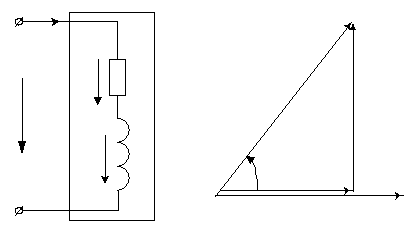
включенных индуктивности![]() и активного сопротивления
и активного сопротивления![]() (рис.6,а).
(рис.6,а).
а) б)
Рис.6
На
рис.6,б представлена векторная диаграмма
для такой катушки. В качестве исходного
выбран вектор тока
![]() ;
вектор напряжения
;
вектор напряжения![]() совпадает по фазе с
совпадает по фазе с![]() ,
,![]() опережает
опережает![]() на угол
на угол![]() .
.![]()
Из рассмотрения треугольника напряжений
![]() .
.
Учитывая,
что
![]() ,
,![]() где
где![]() , получим
, получим
![]() ,
,
где
![]() - полное сопротивление катушки.
- полное сопротивление катушки.
Угол сдвига по фазе между током и напряжением на катушке
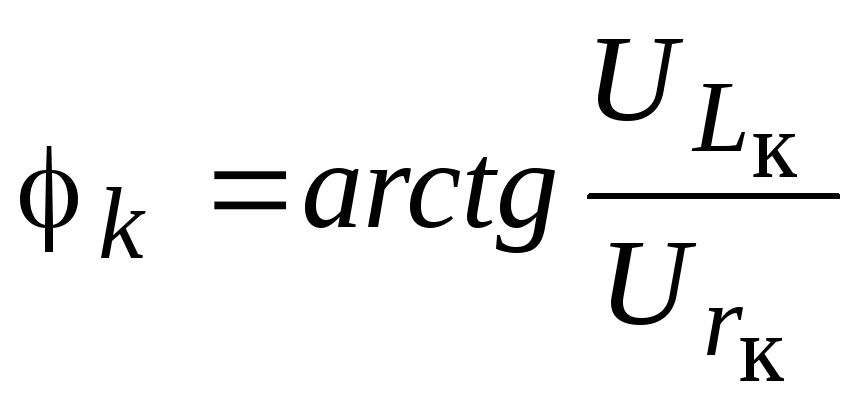
![]() .
.
Параметры эквивалентной схемы можно определить по результатам эксперимента. Измеряя амперметром ток в катушке, вольтметром напряжение на катушке и ваттметром активную мощность, потребляемую в катушке, причем показания ваттметра
![]()
![]() .
.
Определяем
![]() ,
,![]() ,
,![]() ,
,![]() .
.
1.5. Последовательное соединение катушки индуктивности
и емкости
Если к зажимам источника электроэнергии с синусоидально изменяющимся напряжением присоединить последовательно соединенные катушку индуктивности и емкость, то ток и напряжение на элементах цепи будут также синусоидальными и могут быть представлены с помощью векторов.
Катушка индуктивности в этом случае представляется эквивалентной схемой (рис.6,а).
Расчетная
схема и векторная диаграмма при
![]() изображены на рис.7,а, б.
изображены на рис.7,а, б.

а б
Рис.7
Второй закон Кирхгофа для этой схемы в векторной форме
![]() .
.
Напряжение
на емкости
![]() и отстает от тока на
и отстает от тока на![]() .
.
Из диаграммы следует
![]() ,
,
где
![]() -
полное сопротивление цепи;
-
полное сопротивление цепи;
![]() -
реактивное сопротивление;
-
реактивное сопротивление;
![]() -
угол сдвига по фазе между
-
угол сдвига по фазе между
входным напряжением и током.
Резонанс
напряжений.
При равенстве реактивных сопротивлений
![]() в цепи имеет место резонанс напряжений.
При этом напряжения на индуктивности
эквивалентной схемы катушки
в цепи имеет место резонанс напряжений.
При этом напряжения на индуктивности
эквивалентной схемы катушки![]() и на емкости
и на емкости![]() равны по величине и противоположны по
фазе (рис.8), а ток имеет
равны по величине и противоположны по
фазе (рис.8), а ток имеет
наибольшее про заданном напряжении значение
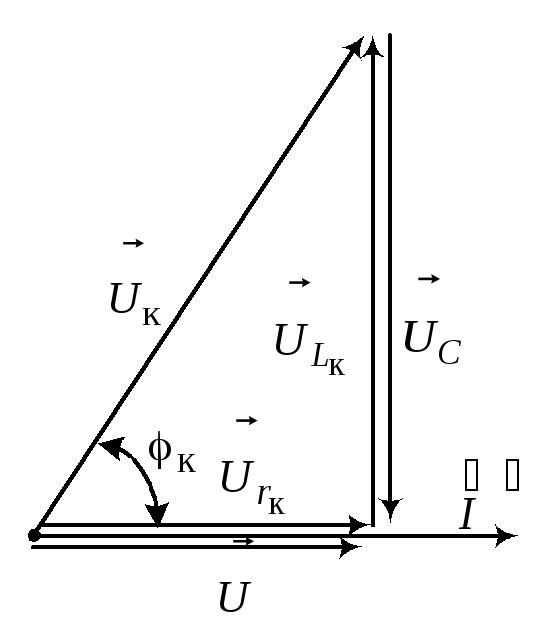
![]()
и
совпадает по фазе с напряжением на
входе схемы. При
![]() напряжения на реактивных элементах
напряжения на реактивных элементах![]() и
и![]() будут существенно превышать величину
подведенного к цепи
напряжения.
будут существенно превышать величину
подведенного к цепи
напряжения.
Рис.8
1.6. Параллельное соединение катушки индуктивности
и емкости
Расчетная схема и векторная диаграмма для этого случая изображены на рис.9, а, б.
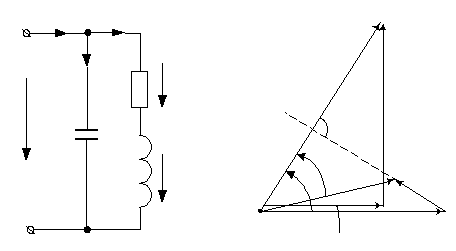
а) б)
Рис.9
При
построении диаграммы учтено, что к
емкости и к катушке индуктивности
приложено одинаковое напряжение
![]() .
.
В качестве исходного при построении
диаграммы (рис.9,б) принят вектор тока в
катушке
![]() .
Напряжения
.
Напряжения![]() ,
,![]() ,
,![]() образуют треугольник напряжений,
аналогичный рис.6,б. Треугольник токов
образуют треугольник напряжений,
аналогичный рис.6,б. Треугольник токов![]() ,
,![]() ,
,![]() соответствует уравнению, составленному
по первому закону Кирхгофа, для узла
схемы, рис.9,а,
соответствует уравнению, составленному
по первому закону Кирхгофа, для узла
схемы, рис.9,а,![]() .
.
Ток
![]() опережает вектор напряжения
опережает вектор напряжения![]() на
угол
на
угол![]() .
.
При
известных![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]() .
.
Ток
![]() определяется по диаграмме, изображенной
на рис.9,б и построенной в масштабе.
определяется по диаграмме, изображенной
на рис.9,б и построенной в масштабе.
Расчет тока
![]() можно выполнить также аналитически,
для этого ток
можно выполнить также аналитически,
для этого ток![]() (рис.10,а) удобно представить в виде
(рис.10,а) удобно представить в виде
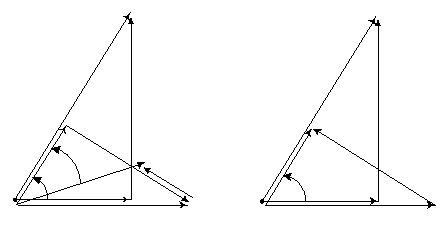
а б
Рис.10
суммы двух составляющих
![]() и
и![]() .
.
Из
![]()
![]()
![]()
![]()
Из
![]()
![]() с учетом
с учетом![]() ,
получим
,
получим
![]()
![]()
,
Множители у напряжения имеют размерность проводимостей.
О![]()
![]() бозначая
бозначая
,
![]()
и, кроме того, получим
![]()
![]()
![]()
Из
![]()
![]()
![]()
![]()
![]()
при т.е. в схеме рис.9,а
наблюдается резонанс токов
![]()
В![]() екторная
диаграмма для этого случая изображена
на рис.10,б.
екторная
диаграмма для этого случая изображена
на рис.10,б.
Т![]() ок
ок
![]() имеет минимальное значение
и совпадает по фазе с напряжением
имеет минимальное значение
и совпадает по фазе с напряжением
![]() .
Если
.
Если![]() ,
то токи
,
то токи![]() и
и
могут
существенно превышать
![]() .
.
1.7. Построение векторных диаграмм по результатам
эксперимента
При
экспериментальном исследовании
последовательного и параллельного
соединения катушки индуктивности и
конденсатора необходимо построить
векторные диаграммы по опытным данным.
Особенность такого построения в том,
что в ходе эксперимента измеряются для
схемы рис. 7,а
![]() ,
,![]() ,
,![]() ,
,![]() ,
а для схемы рис.9,а
,
а для схемы рис.9,а![]() ,
,![]() ,
,![]() ,
,![]() , т.е. только действующие значения токов
и напряжений, а на диаграмме каждый ток
или напряжение должны иметь определенное
направление. Построения следует выполнять
в следующей очередности.
, т.е. только действующие значения токов
и напряжений, а на диаграмме каждый ток
или напряжение должны иметь определенное
направление. Построения следует выполнять
в следующей очередности.
Для последовательной схемы:
1. Построить качественные диаграммы для случаев
![]()
![]()
![]()
2.
По результатам опытов для каждого случая
с помощью циркуля (засечками) в масштабе
построить треугольник напряжений
![]() ,
,
![]() ,
,![]() ориентировочно располагая эти напряжения
подобно их размещению на соответствующей
качественной векторной диаграмме.
ориентировочно располагая эти напряжения
подобно их размещению на соответствующей
качественной векторной диаграмме.
3. Указать направления векторов напряжения.
4.
Из начала вектора напряжения
![]() провести в масштабе вектор тока
провести в масштабе вектор тока![]() так, чтобы он на угол
так, чтобы он на угол![]() опережал вектор напряжения на емкости
опережал вектор напряжения на емкости![]() .
.
Для параллельной схемы:
1. Построить качественные диаграммы для случаев
![]()
![]()
![]()
2.
По результатам опытов для каждого случая
с помощью циркуля (засечками) в масштабе
построить треугольник токов
![]() ,
,![]() ,
,![]() ориентировочно располагая эти токи
подобно их размещению на соответствующей
качественной векторной диаграмме.
ориентировочно располагая эти токи
подобно их размещению на соответствующей
качественной векторной диаграмме.
3. Указать направления векторов тока.
4.
Из начала вектора
![]() провести в масштабе вектор напряжения
провести в масштабе вектор напряжения![]() так, чтобы он на угол
так, чтобы он на угол![]() отставал от вектора тока в емкости
отставал от вектора тока в емкости![]() .
.![]()
2. Пояснения к лабораторной установке
Элементами исследуемых цепей являются катушка индуктивности и набор конденсаторов.
В работе следует учесть, что катушка индуктивности кроме реактивного обладает еще значительным активным сопротивлением. Лабораторные конденсаторы, используемые в работе, рассматриваются как идеальные емкости. Напряжение от сети переменного тока подводится к исследуемой цепи через ЛАТР (лабораторный автотрансформатор).
Измерение токов и напряжений производится амперметрами и вольтметрами электромагнитной системы, измерение мощности – ваттметром электродинамической системы. Ваттметр имеет токовую обмотку, которая включается последовательно с нагрузкой, и обмотку напряжения, которая включается параллельно нагрузке.
Начало
токовой обмотки обозначено
![]() ,
начало обмотки напряжения
,
начало обмотки напряжения![]() .
Эти зажимы называются генераторными.
.
Эти зажимы называются генераторными.
Следует
обратить внимание на то, что начало
токовой обмотки, обозначенное буквой
![]() ,
присоединяется непосредственно к
проводу, идущему от источника питания.
Генераторные зажимы ваттметра образуют
общую точку, которую располагают на
лицевой панели стенда.
,
присоединяется непосредственно к
проводу, идущему от источника питания.
Генераторные зажимы ваттметра образуют
общую точку, которую располагают на
лицевой панели стенда.
![]() Цена
деления ваттметра определяется по
следующей формуле:
Цена
деления ваттметра определяется по
следующей формуле:
,
где
![]() ,
,![]() – значения напряжения и тока, указанные
на лицевой панели под ватметром;
– значения напряжения и тока, указанные
на лицевой панели под ватметром;![]() – число делений шкалы прибора.
– число делений шкалы прибора.
Вольтметр
V
на схеме рис.12 служит для измерения
напряжения на катушке
![]() и емкости
и емкости![]() .
ВольтметрV
с помощью щупов подсоединяется к зажимам
соответствующих элементов после
установки в цепи тока.
.
ВольтметрV
с помощью щупов подсоединяется к зажимам
соответствующих элементов после
установки в цепи тока.
ПРИ ПОДГОТОВКЕ К ЛАБОРАТОРНОЙ РАБОТЕ НЕОБХОДИМО ОТВЕТИТЬ НА ВОПРОСЫ КОНТРОЛЬНОЙ КАРТЫ.
3. Порядок выполнения работы
3.1. Определение параметров эквивалентной схемы катушки индуктивности.
3.1.1. Собрать цепь по схеме рис.11. Установить в цепи ток, равный 1 А. Показания приборов занести в таблицу 1.
3.1.2. По данным измерений рассчитать параметры эквивалентной схемы катушки индуктивности. Результаты расчета занести в таблицу 1. Построить в масштабе по опытным данным векторные диаграммы тока и напряжений.
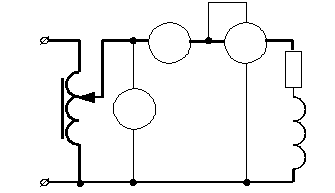
Рис.11
Таблица 1
|
Результаты измерений |
Расчеты на основании результатов измерения | |||||
|
|
|
|
|
|
|
|
|
A |
B |
Вт |
Ом |
Ом |
Ом |
Гн |
|
|
|
|
|
|
|
|
3.2. Последовательное соединение катушки индуктивности и конденсатора. Резонанс напряжений.
Собрать схему рис.12 и произвести измерения в соответствии с рекомендациями, приведенными в п.п.3.2.1 – 3.2.3.
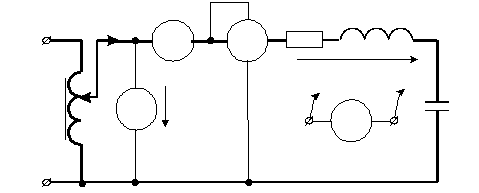
Рис.12
3.2.1.
Установить с помощью набора конденсаторов
емкость, равную расчетной
![]() ,
и
напряжение на входе схемы в соответствии
с контрольной картой. Изменяя (увеличивая
и уменьшая в небольших пределах) емкость
набора конденсаторов, установить режим
резонанса напряжений (т.е. максимальное
значение тока ).
,
и
напряжение на входе схемы в соответствии
с контрольной картой. Изменяя (увеличивая
и уменьшая в небольших пределах) емкость
набора конденсаторов, установить режим
резонанса напряжений (т.е. максимальное
значение тока ).
3.2.2.
Увеличить емкость по сравнению с
величиной, полученной в п.3.2.1, установив
ее величину по контрольной карте.
Установить напряжение
![]() в соответствии с контрольной картой
(третий вариант).
в соответствии с контрольной картой
(третий вариант).
3.2.3.
Уменьшить емкость по сравнению с п.
3.2.1, установив ее величину по контрольной
карте. Установить мощность
![]() в
соответствии с контрольной картой
(второй вариант).
в
соответствии с контрольной картой
(второй вариант).
Различные
значения
![]() и
результаты измерений занести в таблицу
2. Сравнить результаты опытов и расчетов.
и
результаты измерений занести в таблицу
2. Сравнить результаты опытов и расчетов.
3.2.4. По опытным данным построить в масштабе векторные диаграммы токов и напряжений для исследуемых режимов (см.п.1.7.).
Таблица 2
|
Режимы |
|
|
|
|
|
| |
|
мкФ |
Вт |
А |
В |
В |
В | ||
|
|
Опыт 3.2.1 |
|
|
|
|
|
|
|
Расчет
|
|
|
|
|
|
| |
|
|
Опыт 3.2.2 |
|
|
|
|
|
|
|
Расчет
|
|
|
|
|
|
| |
|
|
Опыт 3.2.3 |
|
|
|
|
|
|
|
Расчет
|
|
|
|
|
|
| |
