Эрмитовость оператора импульса

.

Доказательство:

Левая сторона (2.14)

с оператором имеет вид

.

Вычисляем правую сторону (2.14)

.

В результате

.

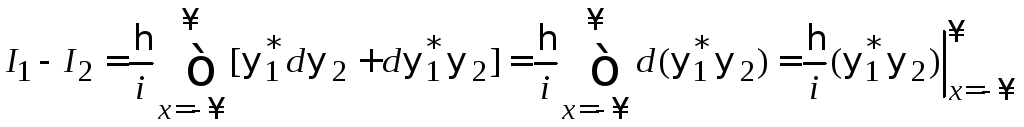Волновые функции квадратично интегрируемы и равны нулю на бесконечности, поэтому , и оператор импульса эрмитов.

УсЛовия ортонормированности

Собственные функции любого эрмитового оператора образуют ортонормированный базис. Спектр базиса зависит оти может быть дискретным или непрерывным. Нормировка ортазависит от вида спектраn. Ортогональность ортов , где, и их нормировку объединяет условие ортонормированности.

Дискретный спектр n. Выполняется нормировка , тогда условие ортонормированности

, (2.21)

где –символ Кронекера. Сходимость интеграла требует достаточно быстрого убывания плотности вероятности за пределами некоторого конечного объема. Следовательно, дискретный спектр соответствует связанному состоянию, и наоборот – связанное состояние имеет дискретный спектр энергии и импульса.

Непрерывный спектр n. Если индекс собственной функции принимает непрерывные значения, то в (2.21) вместо символа Кронекера ставится дельта-функция

. (2.22)

При интеграл стремится в бесконечность. Плотность вероятностиконечна. Чтобы обеспечить требуемое значение интеграла она не может равняться нулю за пределами любого конечного объема. Следовательно,непрерывный спектр соответствует неограниченному движению, и наоборот – состояние неограниченного движения имеет непрерывный спектр энергии и импульса.

Среднее значение величины

Собственные функции эрмитового оператора образуют ортонормированный базис. Если частица находится в состоянии Ψ, являющемся суперпозицией функций, то физическая величинаA не имеет определенного значения. Получим ее среднее значение.

Разложение состояния Ψ по базису имеет вид:

для дискретного спектра

, (2.23)

для непрерывного спектра

, (2.24)

где – комплексное число. Докажем, что коэффициент разложения является амплитудой вероятности обнаружения состоянияв исследуемом состоянии Ψ. Вероятность обнаружения определяет .

Коэффициенты разложения . Умножаемна (2.23) или (2.24), интегрируем по пространственным переменным, переставляем суммирование и интегрирование, учитываем условия ортонормированности (2.21) или (2.22). Для дискретного спектра получаем

,

для непрерывного спектра

.

Заменяем , и для дискретного и непрерывного спектров находим коэффициент разложения

. (2.25)

Определим физический смысл коэффициента . Разложение для дискретного спектраподставляем в условие нормировки функции состоянияи получаем

.

Результат сравниваем с нормировкой вероятности дискретных событий

.

Следовательно, вероятность обнаружения состояния в нормированном состоянии равна квадрату модуля коэффициента разложения

. (2.26)

Разложение для непрерывного спектра

подставляем в условие нормировки функции состояния

,

учитываем ортонормированность (2.22)

,

получаем

.

Результат сравниваем с нормировкой вероятности непрерывных событий

.

Следовательно, плотность вероятности обнаружения состояния в нормированном состоянии равна квадрату модуля коэффициента разложения

. (2.27)

Среднее значение величины, описываемой оператором , в нормированном состоянииравно

. (2.28)

Доказательство:

Состояние разлагаем по собственным функциямоператорас дискретным спектром

,

подставляем в (2.28), учитываем

,

,

получаем

.

Результат совпадает с определением среднего

в теории вероятности дискретной величины.

Для непрерывной величины аналогично находим из (2.28) известное в теории вероятности выражение

.