
- •Математические основы квантовой механики
- •Основные положения
- •Волновая функция
- •ОператорЫ
- •Собственные функции операторА и собственные значения
- •ЭрмитовыЙ оператор
- •Эрмитовость оператора импульса
- •УсЛовия ортонормированности
- •Среднее значение величины
- •СоотношениЕ неопределенностей
- •ОператорЫ трансляции и эволюции
- •Уравнение Шредингера
- •Быстрота Изменения величины
- •Ток вероятности
- •Матрица плотности
Собственные функции операторА и собственные значения
Собственная
функция
![]() оператора
оператора![]() определяется уравнением
определяется уравнением
![]() ,
(2.8)
,
(2.8)
где
![]() –собственное
значение оператора.
Под действием оператора его собственная
функция восстанавливается с точностью
до постоянного множителя, который
называется собственным значением.
–собственное
значение оператора.
Под действием оператора его собственная
функция восстанавливается с точностью
до постоянного множителя, который
называется собственным значением.
Физический
смысл собственного значения – если
система находится в состоянии
![]() ,
то измерение величиныA,
описываемой оператором
,
то измерение величиныA,
описываемой оператором
![]() ,
дает однозначный результат
,
дает однозначный результат![]() .
Собственные функции с разными собственными
значениями взаимно ортогональны. Это
исключает возможность получить при
измерении неоднозначный результат.
.
Собственные функции с разными собственными
значениями взаимно ортогональны. Это
исключает возможность получить при
измерении неоднозначный результат.
Спектр
оператора
– это множество его собственных значений
![]() .
.
Если
![]() счетное, тоспектр
дискретный.
счетное, тоспектр
дискретный.
Если
![]() образует непрерывный набор, тоспектр
непрерывный.
образует непрерывный набор, тоспектр
непрерывный.
Если k разных собственных функций имеют одинаковые собственные значения, то спектр k-кратно вырожден.
Коммутирующие операторы имеют одинаковый набор собственных функций, соответствующие физические величины одновременно имеют определенные значения.
Доказательство:
Пусть
![]() – собственная функция
– собственная функция![]() ,
тогда
,
тогда
![]() .
.
Действуем
оператором
![]() на обе стороны равенства
на обе стороны равенства
![]() .
.
Учитываем коммутативность операторов
![]() ,
,
получаем
![]() .
.
Следовательно,
![]() – собственная функция
– собственная функция![]() ,
пропорциональная
,
пропорциональная![]() :
:
![]() .
.
Полученное
равенство означает, что
![]() – собственная функция
– собственная функция![]() с собственным значением
с собственным значением![]() .
.
Оператор
координаты
![]() .
Пусть
.
Пусть![]() – собственная функция с собственным
значением
– собственная функция с собственным
значением![]() ,
тогда
,
тогда

Верхнее равенство является определением оператора координаты, нижнее – определением собственной функции и собственного значения. В результате
![]()
Сравниваем с фильтрующим свойством дельта-функции
![]() ,
,
находим
![]() .
.
Функция
![]() равна нулю во всех точках, кроме
равна нулю во всех точках, кроме
![]() ,
гдеx0
– любое вещественное число, поэтому
спектр x0
непрерывный.
Вид функции согласуется с физическим
смыслом состояния – частица обнаруживается
в точке x0.
В результате обоснована форма оператора
координаты.
,
гдеx0
– любое вещественное число, поэтому
спектр x0
непрерывный.
Вид функции согласуется с физическим
смыслом состояния – частица обнаруживается
в точке x0.
В результате обоснована форма оператора
координаты.
Как показано далее условие ортонормированности для непрерывного спектра имеет вид
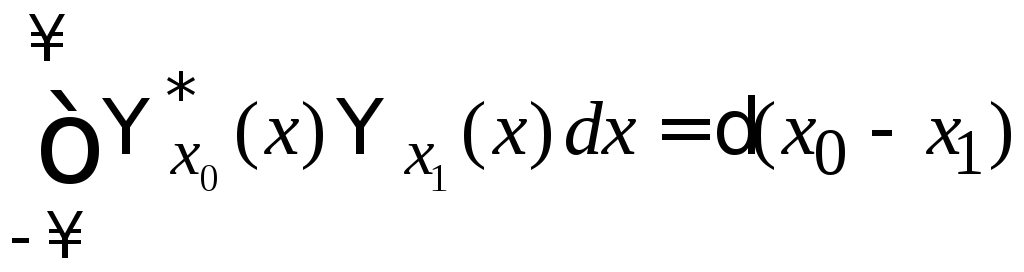 .
.
Подстановка
![]() дает
дает
 .
.
Откуда
![]() ,
тогдасобственная
функция оператора координаты, или
волновая функция частицы, находящейся
в точке x0,
есть
,
тогдасобственная
функция оператора координаты, или
волновая функция частицы, находящейся
в точке x0,
есть
![]() .
(2.9)
.
(2.9)
Оператор
проекции импульса
![]() .
Уравнение на собственную функцию дает
.
Уравнение на собственную функцию дает

Получили дифференциальное уравнение первого порядка
 .
.
Разделяем переменные
 ,
,
интегрируем
![]() ,
,
находим
 .
.
Результат совпадает с координатной зависимостью плоской волны де Бройля
 ,
(1.11)
,
(1.11)
описывающей движение частицы с постоянным импульсом. В результате обоснована форма оператора импульса. Поскольку p – любое вещественное число, то спектр непрерывный. Условие ортонормированности для непрерывного спектра

дает
 .
.
Используя
 ,
,
находим
![]() .
В результатесобственная
функция оператора импульса, или
волновая
функция частицы, движущейся с импульсом
p,
равна
.
В результатесобственная
функция оператора импульса, или
волновая
функция частицы, движущейся с импульсом
p,
равна
 .
(2.10)
.
(2.10)
ЭрмитовыЙ оператор
Для обеспечения вещественности и однозначности результатов измерения физической величины ее оператор должен быть эрмитовым. Операция эрмитового сопряжения определяется через интегральную квадратичную форму. Такая форма описывает, в частности, среднее значение измеряемой величины.
Эрмитово
сопряженный оператор
![]() обозначается значком «+»
и определяется в виде
обозначается значком «+»
и определяется в виде
![]() .
(2.11)
.
(2.11)
Интегрирование проводится по всему объему пространства, занятого частицей.
Свойства эрмитового сопряжения
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
(2.12)
.
(2.12)
Действительно,
![]() ,
,
![]() ,
,
где выполнено эрмитовое сопряжение первого оператора, а затем второго оператора.
Эрмитовый оператор не изменяется при эрмитовом сопряжении
![]() .
(2.13)
.
(2.13)
Из (2.11) получаем
![]() .
(2.14)
.
(2.14)
Свойства эрмитова оператора:
1) Собственные значения вещественные.
Доказательство:
В
(2.14) полагаем
![]() ,
где
,
где![]() – собственная функция оператора
– собственная функция оператора![]() ,
учитываем
,
учитываем
![]() ,
,
![]() ,
,
получаем
![]() .
.
Следовательно,
![]() (2.15)
(2.15)
– измеряемая величина вещественна.
2) Собственные функции, соответствующие разным собственным значениям, взаимно ортогональны.
Доказательство:
Пусть
![]() ,
,
![]() ,
,![]() ,
,![]() .
.
Из
(2.14) при
![]() ,
,![]() получаем
получаем
![]() .
.
Учитывая (2.15), находим
![]() .
.
При
![]() выполняетсяусловие
ортогональности
выполняетсяусловие
ортогональности
![]() .
(2.16)
.
(2.16)
– состояния
![]() и
и![]() при измерении не совместимы.
при измерении не совместимы.
