
- •Глава 3. Элементы аналитической геометрии
- •§3.1. Аналитическая геометрия на плоскости
- •3.1.1. Метод координат
- •3.1.2. Понятие об уравнении линии на плоскости
- •3.1.3. Прямая линия на плоскости
- •3.1.4. Кривые второго порядка
- •§3.2. Аналитическая геометрия в пространстве
- •3.2.1. Плоскость
- •30. Частные случаи уравнений плоскости.
- •3.2.2. Прямая в пространстве
- •3.2.3. Взаимное расположение прямых и прямой и плоскости в пространстве
3.2.2. Прямая в пространстве
10. Линия в пространстве и ее уравнение. В аналитической геометрии любая линия в пространстве рассматривается как множество точек пересечения двух поверхностей. Отсюда, система уравнений
![]() (3.39)
(3.39)
определяет (вообще говоря)
некоторую линию
![]() в пространстве.
в пространстве.
Таким образом, каждая линия задается системой (3.39) двух уравнений с тремя переменными, а каждая совместная система (3.39) определяет некоторую линию.
Здесь также (как и на плоскости) основными считаются две задачи: а) дана система уравнений вида (3.39), найти определяемую ими линию; б) дана линия, найти определяющую ее систему уравнений.
Пример. Система линейных
уравнений определяет прямую линию, проходящую
через точку
определяет прямую линию, проходящую
через точку![]() и параллельную оси
и параллельную оси![]() ,
ибо первое уравнение системы определяет
плоскость, параллельную плоскости
,
ибо первое уравнение системы определяет
плоскость, параллельную плоскости![]() ,
а второе – плоскость, параллельную
плоскости
,
а второе – плоскость, параллельную
плоскости![]() .
.
20. Общее уравнение прямой. Из п.10следует, что прямую в пространстве можно определить как общую часть двух плоскостей
 (3.40)
(3.40)
Система (3.40) называется системой
общих уравнений прямой. Конечно,
предполагается, что нормальные к
плоскостям
![]() и
и![]() векторы
векторы![]() и
и![]() не коллинеарны (то есть
не коллинеарны (то есть![]()
![]()
![]()
![]() ).
).
Замечание 1. Одну и ту же прямую, очевидно, можно задать различными системами общих уравнений.
Замечание 2. Отдельно взятые коэффициенты каждого из уравнений системы (3.40) не связаны с положением прямой относительно системы координат, что ограничивает использование ее в конкретных задачах.
30. Канонические
уравнения прямой. Задать прямую![]() в пространстве можно точкой лежащей на
ней точкой:
в пространстве можно точкой лежащей на
ней точкой:![]()
![]() и, так называемым, «направляющим вектором»
ее
и, так называемым, «направляющим вектором»
ее![]() (
(![]() ).
).
Чтобы в этом случае составить
уравнение прямой, возьмем текущую точку
ее
![]()
![]() и построим вектор
и построим вектор![]() (рис.3.29 хх ). Очевидно, в таком случае,
векторы
(рис.3.29 хх ). Очевидно, в таком случае,
векторы![]() ║
║![]() ,
а для любой точкиM,
не лежащей на прямой, коллинеарность
не имеет места.
,
а для любой точкиM,
не лежащей на прямой, коллинеарность
не имеет места.
Запишем условие коллинеарности векторов в координатной форме (см.§2.2,п.80, формула (2.30)):
![]() .
(3.41)
.
(3.41)
Уравнения (3.41) называются каноническими уравнениями прямой.
Пример. Прямую, заданную общими уравнениями прямой (см. пример из п.10) записать в каноническом виде.
Решение. Прямая параллельна
оси![]() ;
следовательно, в качестве направляющего
вектора
;
следовательно, в качестве направляющего
вектора![]() можно взять орт
можно взять орт![]() :
:![]() =
=![]() =
=![]() .
Запишем канонические уравнения прямой
(3.41):
.
Запишем канонические уравнения прямой
(3.41):![]() (см. также замечание к формуле (3.10’),
п.3.1.3, 20).
(см. также замечание к формуле (3.10’),
п.3.1.3, 20).
40. Уравнения
прямой, проходящей через две заданные
точки. Пусть прямая![]() проходит через две заданные точки
проходит через две заданные точки![]() и
и![]() .
За направляющий вектор
.
За направляющий вектор![]() этой прямой возьмем вектор
этой прямой возьмем вектор![]() :
:![]() =
=![]() =
=![]() .
Взяв за точку, лежащую на прямой, точку
.
Взяв за точку, лежащую на прямой, точку![]() ,
запишем для прямой
,
запишем для прямой![]() канонические уравнения (3.41):
канонические уравнения (3.41):
![]() .
(3.42)
.
(3.42)
Следствие. Для того, чтобы
три точки![]() лежали на одной прямой, необходимо и
достаточно, чтобы
лежали на одной прямой, необходимо и
достаточно, чтобы
![]() .
(3.43)
.
(3.43)
50. Параметрические
уравнения прямой. Пусть прямая![]() задана каноническими уравнениями
(3.41). Тогда для любой точки
задана каноническими уравнениями
(3.41). Тогда для любой точки![]()
![]() дроби из (3.41) имеют определенное значение
(свое для
дроби из (3.41) имеют определенное значение
(свое для![]() );
обозначим эти отношения черезt.
Тогда
);
обозначим эти отношения черезt.
Тогда
![]() ,
,
откуда
![]() (3.44)
(3.44)
– уравнения прямой
![]() в параметрической форме. В (3.44) параметрtменяется в пределах
от
в параметрической форме. В (3.44) параметрtменяется в пределах
от![]() до
до![]() .
.
Замечание. Умножая первое
уравнение из (3.44) на орт![]() ,
второе – на
,
второе – на![]() и третье – на
и третье – на![]() и складывая результаты, придем к
векторному уравнению прямой
и складывая результаты, придем к
векторному уравнению прямой
![]() .
(3.45)
.
(3.45)
60. Приведение общих уравнений прямой к каноническому виду.Решение этой задачи складывается из двух этапов.
1) найдем направляющий вектор
![]() прямой. Очевидно, вектор
прямой. Очевидно, вектор![]() |
| ![]() и
и![]() |
| ![]() (перпендикулярен каждому из направляющих
векторов
(перпендикулярен каждому из направляющих
векторов![]() и
и![]() плоскостей
плоскостей![]() и
и![]() ,
определяемых уравнениями (3.40).
,
определяемых уравнениями (3.40).
Одним из таких векторов есть
векторное произведение направляющих
векторов
![]() и
и![]() :
:
![]() =
=![]()
![]()
![]() =
=
![]() .
(3.46)
.
(3.46)
2) найдем точку
![]() .
По крайней мере, одна из координат
вектора
.
По крайней мере, одна из координат
вектора![]() отлична от нуля; пусть это координата
отлична от нуля; пусть это координата![]() .
Полагая в уравнениях (3.40)
.
Полагая в уравнениях (3.40)![]() ,
придем к системе из двух уравнений с
двумя неизвестными с главным определителем
,
придем к системе из двух уравнений с
двумя неизвестными с главным определителем![]() :
:
 (3.47)
(3.47)
Система (3.47) имеет некоторое
(единственное) решение
![]() и точка
и точка![]() и есть искомая точка. Рассмотрим пример.
и есть искомая точка. Рассмотрим пример.
Пример. Написать канонические
уравнения прямой![]() ,
заданной общими уравнениями
,
заданной общими уравнениями![]() .
.
Решение. Найдем по формуле
(3.46) направляющий вектор прямой![]() – вектора
– вектора![]() (здесь нормальные векторы имеют вид:
(здесь нормальные векторы имеют вид:![]() ,
,![]() ):
):
![]() =
=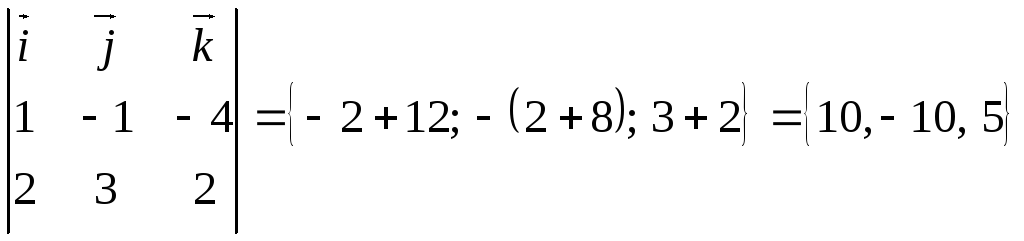 .
.
Составим систему (2.40), полагая
![]() ;
имеем систему
;
имеем систему![]() ,
,![]() ,
решение которой
,
решение которой![]() ,
,![]() .
По (3.41) пишем канонические уравнения
прямой
.
По (3.41) пишем канонические уравнения
прямой![]() :
:![]() .
.
