Глава 2. Предел числовой последовательности

2.1. Определение окрестности точки, числовой

последовательности и ее предела

2.1.1. Числовая последовательность

1. Что называется числовой последовательностью? Как обозначается и каким образом задается числовая последовательность. Приведите примеры числовых последовательностей.

2. Какая последовательность называется постоянной последовательностью, конечной последовательностью? Приведите примеры таких последовательностей.

3. Приведите примеры геометрической и арифметической прогрессий.

4. Найдите пятый член последовательностей:

а) , если,

б) , если,

в) , если,,

г) ,

д) − последовательность всех делителей числа 20, расположенных в порядке возрастания,

е) ,

ж) − последовательность,n член которой − n цифра числа ,

з) ,

и) − геометрическая прогрессия, у которой первый член, а знаменатель прогрессии,

к) − арифметическая прогрессия, у которой первый член, а разность прогрессии.

5. Дайте определения ограниченной сверху (снизу), ограниченной, неограниченной последовательности. Каков геометрический смысл понятия “ограниченная последовательность”? Приведите соответствующие примеры.

6. Являются ли последовательности ограниченными сверху (снизу), ограниченными, неограниченными:

а) ,

б) ,

в) ,

г) ,

д) .

2.1.2. Предел числовой последовательности

1. Запишите определение предела последовательности с помощью логических знаков.

2. Дайте определения сходящейся и расходящейся последовательности. Приведите примеры таких последовательностей.

3. Пусть последовательность и числоудовлетворяют условию:

такое, что . Всякая ли сходящаяся кпоследовательность удовлетворяет этому условию?

4. Пусть .

а) Могут ли все члены последовательности быть положительными (отрицательными), если ?

б) Может ли последовательность иметь бесконечно много отрицательных (равных нулю) членов, если ?

в) Докажите, что ,.

5. Пусть последовательность сходится. Является ли сходящейся последовательность, которая получается из исходной, если:

а) из нее удалить конечное число членов, а оставшиеся заново перенумеровать в порядке их следования,

б) к ней добавить конечное число членов, перенумеровав члены последовательности в порядке их следования,

в) в ней изменить произвольным образом конечное число членов?

6. Сформулировать на языке “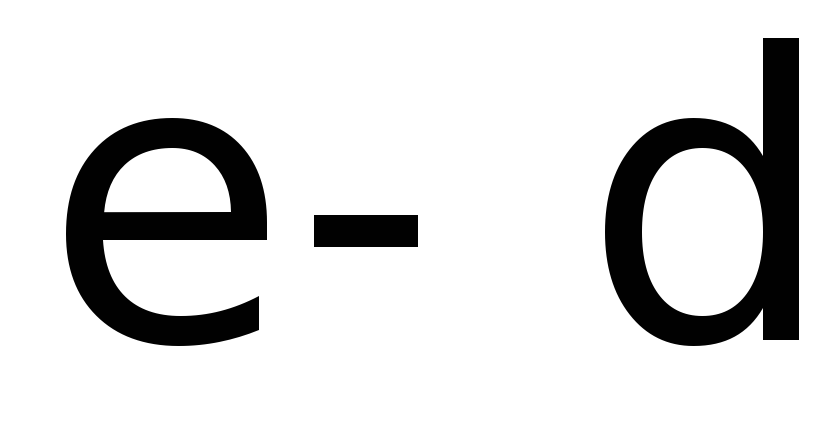”определение того, что

а) ,

б) не существует .

7. Докажите по определению, что предел равен.

8. Докажите, что если , то.

9. Привести пример последовательности , удовлетворяющей условиюи такой, что

а) она не имеет предел,

б) она имеет предел. Может ли этот предел быть положительным?

2.1.3 Окрестность точки, геометрический смысл предела последовательности

1. Дайте определение окрестности точки .

2. Приведите геометрическую иллюстрацию предела последовательности.

3. Пусть в некоторой окрестности точки лежит бесконечно много членов последовательности. Следует ли из этого условия, что:

а) ,

б) никакая точка вне этой окрестности не является пределом последовательности ,

в) ограничена?

4. Пусть в любой окрестности точки лежит бесконечно много членов последовательности. Следует ли отсюда, что?