Вариант3

Вариант № 3

В задачах 1…9 найти неопределённые интегралы, ответ проверить дифференцированием.

1. .

Проверка: .

Ответ: .

2. . Интегрируем дважды по частям: . .

Проверка:

. Ответ: .

3.

. Проверка:

. Ответ: .

4. . Выделяем целую часть и разлагаем дробную часть на простые дроби.

. Полагаем , получим . Из равенства следует . Приравнивая коэффициенты при , получим . Или . Таким образом,

Проверка: . Ответ: .

5. . Вычисляем интеграл с помощью предварительных преобразований. . Проверка: . Ответ: .

6. . Интегрируем с помощью замены переменной.

.

Проверка: . Ответ: .

7. . Интегрируем с помощью замены переменной. . Или

. Проверка:

. Ответ: .

8. . Интегрируем с помощью замены переменной. .

Проверка: .

Ответ: .

9. . Интегрируем с помощью универсальной подстановки.

. Проверка:

. Ответ: .

Задачи 10-11. Вычислите несобственные интегралы или установите их расходимость.

10. . Интеграл расходится.

Ответ: . Интеграл расходится.

11.

. Интеграл сходится. Ответ: . Интеграл сходится.

Задачи 12-13. Вычислите площадь фигуры, ограниченной линиями.

1 2. 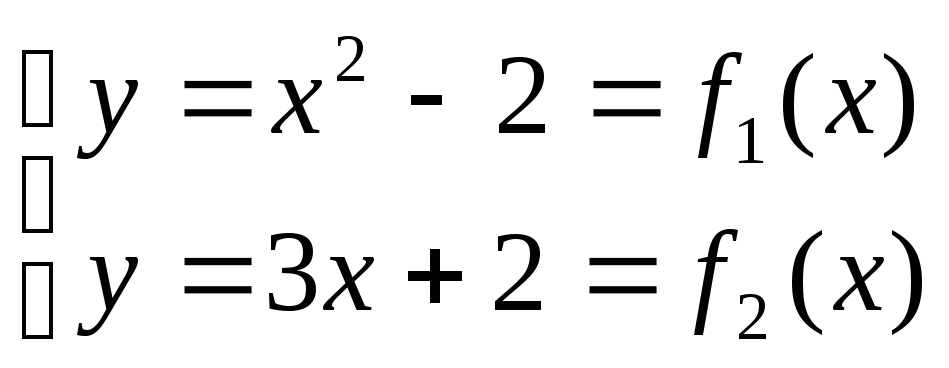. Найдём точки пересечения линий: .

Тогда . Ответ: .

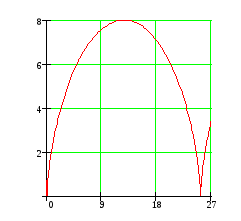1 3. . Фигура ограничена снизу . Найдём соседние точки пересечения с прямой : . Вычисляем площадь: . Ответ: .

14. Вычислите длину дуги кривой (L): (кардиоида).

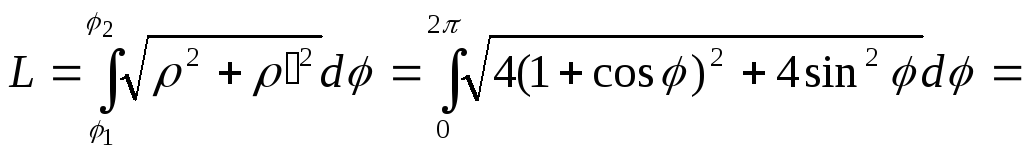
.Ответ: .

15. Найдите объём тела вращения плоской фигуры (S) вокруг оси OX.

Найдём точки пересечения линий: .

. Ответ: .

16. Вычислите площадь поверхности вращения дуги (L) вокруг оси OX.

. Ответ: .

Задачи 17…18. Вычислите интегралы, воспользовавшись справочниками по высшей математике.

17. . По справочнику находим: .

Ответ: . (Г.Б. Двайт. Таблицы интегралов и другие математические формулы.)

18. . По справочнику находим: . В данном случае . Следовательно, . Ответ: .

19. Ракетный снаряд поднимается вертикально вверх. Ускорение ракеты за счёт уменьшения веса растёт по закону (a, b, A – положительные постоянные, a-bt>0). Найдите скорость ракеты в момент t=t₁, если её начальная скорость равна нулю.

. В момент t₁ скорость будет равна . Ответ: .

2 0. Какую работу нужно произвести, чтобы насыпать кучу песка в форме усечённого конуса высоты H , имеющего радиусы оснований R и r ? Удельный вес песка γ . Песок поднимают с поверхности земли, на которой покоится большое основание конуса (R > r ).

Уравнение образующей конуса . Или . Элементарный объём песка имеет вес . Элементарная работа по поднятию этого песка на высоту y равна . Тогда