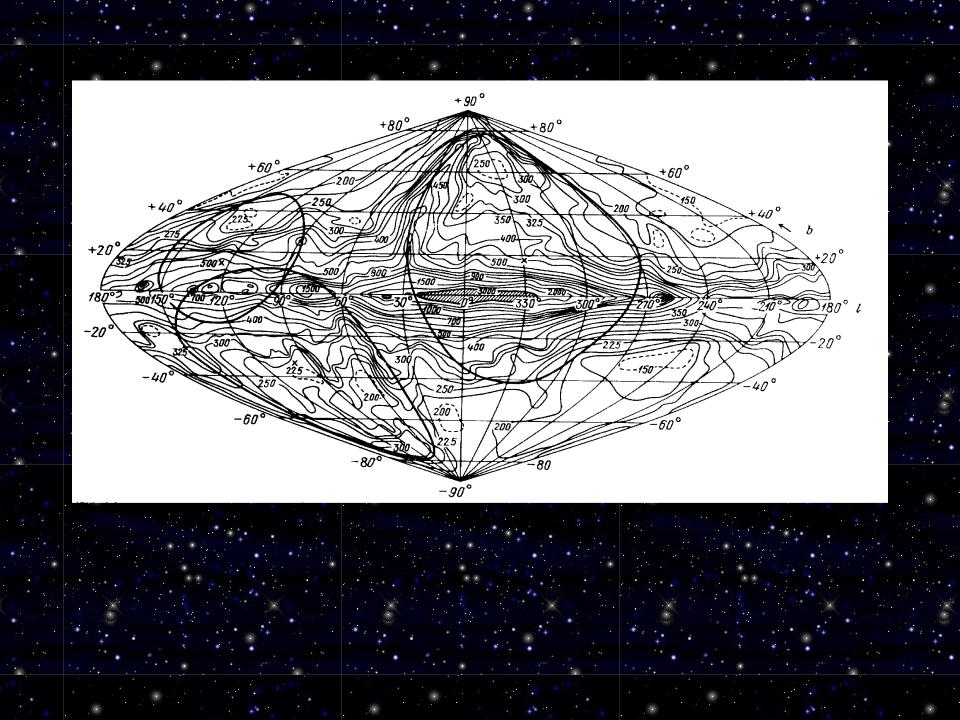
Изофоты радиоизлучения Галактики на частоте 150 МГц
Распределение по небу нейтрального водорода (по данным обзоров в линии 21 см). Видна резкая концентрация его к галактической плоскости.
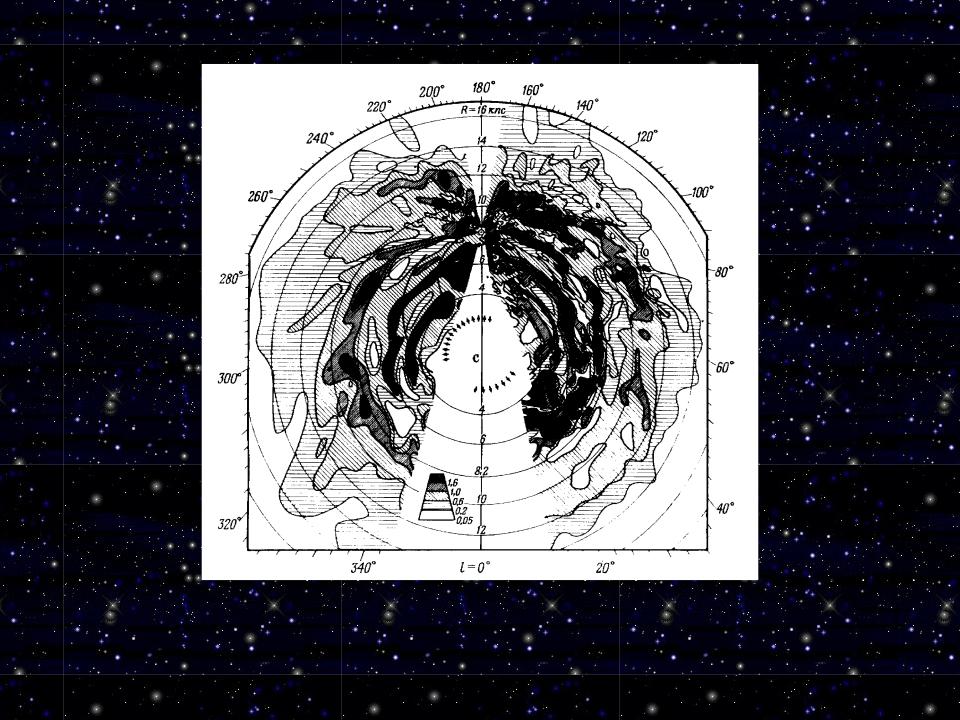
Распределение нейтрального водорода в плоскости Галактики по данным Лейденского обзора в линии 21 см
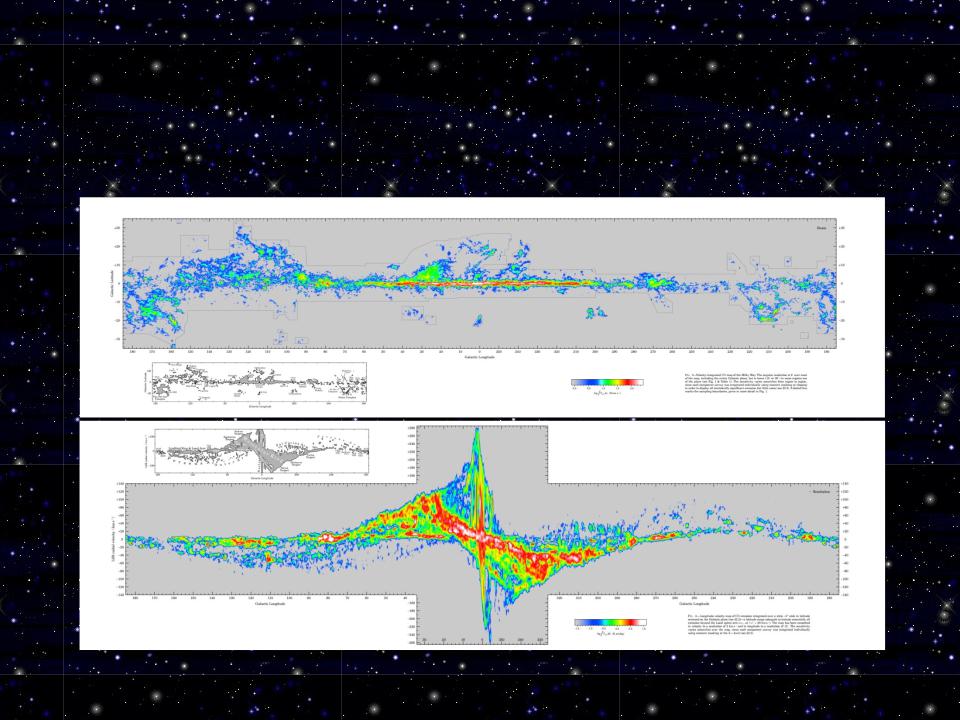
Распределение молекулярного газа в Галактике: обзоры в линии СО
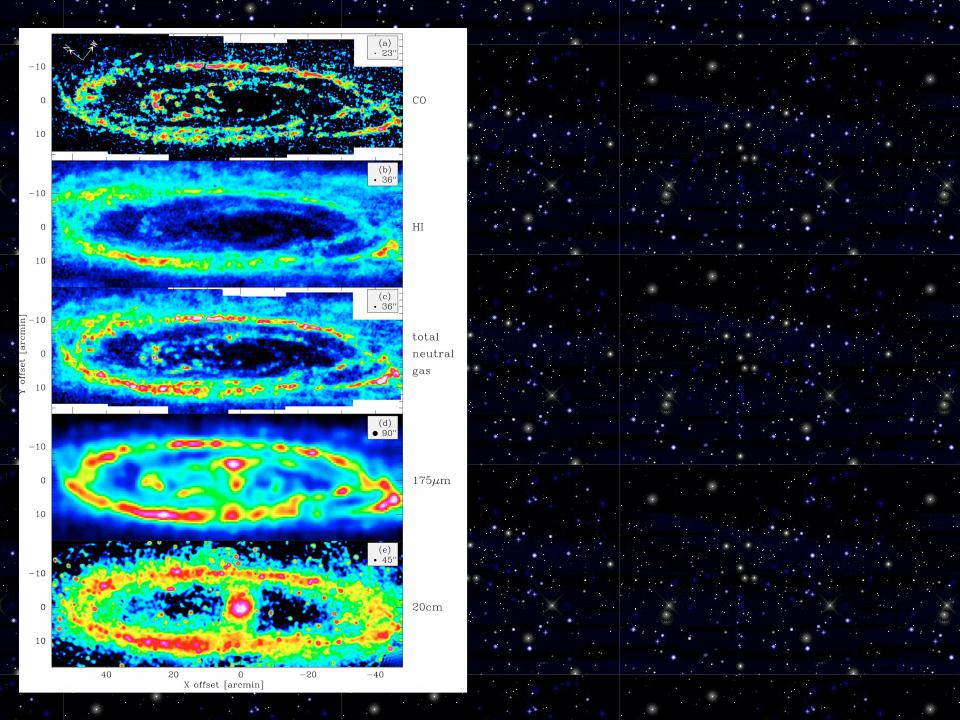
Межзвёздная среда в других галактиках
Распределение молекулярного газа в М31 по данным наблюдений CO(1-0) на 30-м радиотелескопе IRAM в сравнении с распределением атомарного водорода, излучения пыли и радиоконтинуума.
Межзвездная газодинамика
•Длина свободного пробега атомов и молекул в межзвездной среде, 1/σn, << характерных масштабов большинства объектов, так что к ним применимы принципы гидродинамики (σ ~ 10-15 см2).
•Во многих случаях существенно влияние магнитного поля, так что необходимо использовать уравнения магнитной гидродинамики.
Теорема вириала
Для стационарной системы выполняется
соотношение:
2T U 0
T кинетическая энергия |
||
U гравитационная энергия |
||
2T U M 0 |
С учетом магнитного поля |
|
M 1 H 2 R3 |
||
|
||
6 |
|
|
Часто используется понятие вириальной массы,
которая определяется из этого уравнения (по |
||
данным о размере и дисперсии скоростей |
||
источника). |
Mvir R V |
2 |
|
||
|
|
|
Волновые движения в МЗС
•В отсутствие магнитного поля в МЗС могут распространяться звуковые волны.
•При наличии магнитного поля в газе распространяются волны трех видов:
– магнитогидродинамические или
альвеновские V 2 B2
A 4
– быстрые магнитозвуковые
– медленные магнитозвуковые
Ударные фронты
Условия на разрыве (B = 0):
1u1 2u2
p1 1u12 p2 2u22
u |
2 |
1 |
|
u2 |
U |
|
u |
1 |
u2 |
U |
|
u p u |
2 |
p |
2 |
||
|
|
2 |
2 |
2 |
|
2 |
1 |
|
2 |
1 1 |
|
1 |
1 1 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
U |
p |
|
внутренняя энергия |
|
1 |
||||
|
|
|||
При больших числах |
2 |
1 |
|
|
|
|
|
|
|
|
|||
Маха |
1 |
1 |
|
|
|
|
При γ = 5/3 ρ2/ρ1 |
|
|
2 |
|
u12 |
|
= 4 |
|
|
|
2 |
||
|
|
|
C2 |
|||
Для изотермической |
|
|
|
M |
||
ударной волны |
|
1 |
|
s |
|
|
|
|
|
|
|||
Основные неустойчивости МЗС
Гравитационная |
|
|
|
|
|
|
|||||||||||||||||
неустойчивость |
|
|
|
|
|
|
|||||||||||||||||
(неустойчивость2 2 2 |
Джинса) |
|
|||||||||||||||||||||
|
Cs k |
4 G |
Дисперсионное уравнение для |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
«тяжелого» звука |
1/ 2 |
|||||||
|
|
|
|
|
|
|
Cs |
|
|
|
|
|
|
|
3 3 |
||||||||
J |
2 |
|
|
1.6пк |
|
T |
10см |
|
|||||||||||||||
|
G |
|
|
|
n |
||||||||||||||||||
|
|
kJ |
|
|
|
|
|
|
|
|
|
10K |
|
|
|||||||||
|
|
|
|
|
|
|
3 |
|
3 |
|
1/ 2 |
|
|
|
|
|
|
||||||
|
|
0.8пк |
T |
|
|
10см |
|
|
|
|
|
|
|
|
|
||||||||
J |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|||||||
|
|
10K |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
T |
|
|
3/ 2 |
|
|
3 |
|
3 1/ 2 |
|
|
|
|||||||
|
|
|
|
|
|
|
10см |
|
|
|
|
|
|||||||||||
M J 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Me |
|
|||||||
|
|
|
|
|
|
|
|
|
n |
|
|
||||||||||||
|
|
|
10K |
|
|
|
|
|
|
|
|
|
|||||||||||