С учетом сказанного имеет место разложение

(6.13)

называемое рядом Тейлора функции f(x) в точке х₀.

Если в (6.13) положить х₀ = 0, то получим ряд

(6.14)

который является частным случаем ряда Тейлора и называется рядом Маклорена.

Пример 1. Разложить в ряд Тейлора функции

1. f(x) = ln x в окрестности точки х₀ = 1.

2. f(x) =2^x в окрестности точки х₀ = 2.

Решение

1. Вычислим значения функции ln x и ее производных в точке х₀ = 1 и воспользуемся разложением (5.13):

f(x) = ln x , f(1) = ln 1 = 0;

;

;

;

;

=24;

……………

Тогда

,

или

2. Найдем значения функции 2^х и ее производных в точке х₀ = 2.

. . . . . . . . . .

Подставляя полученные выражения в формулу (6.13), получим искомое разложение:

или

Пример 2. Разложить в ряд Маклорена функцию f(x) = e^x.

Решение. Найдем значения функции e^x и ее производных в точке x₀ =0.

Известно, что

и, следовательно, .

Тогда из формулы (6.14) получим

.

Аналогично можно получить разложения

;

;

(R, 1 < x < 1).

Последнее разложение называется биномиальным рядом. В случае, когда   натуральное число,  = n  N, этот ряд представляет собой формулу бинома Ньютона.

.

Пример 3. Разложить в ряд Маклорена функцию .

Решение. В разложении

заменим t на – х², получим

или

.

Разложить в ряд Маклорена функции:

97. 98.

99. 100.

101. 102.

103. 104.

105. 106.

Разложить в ряд Тейлора функции в окрестности заданных точек

107.

108.

109. x₀ = 2

110. , x₀ =

§6. Применение степенных рядов

к приближенным вычислениям

1. Приближенные вычисления значений функций

Вычисление приближенного значения функции f(x) основано на использовании приближенного равенства f(x)  S_n(x), где S_n(x) – частичная сумма степенного ряда, в который раскладывается данная функция. Для определения погрешности найденного приближенного значения, нужно оценить сумму отброшенных членов ряда или его остатка r_n(x).

Известно, что погрешность приближенного равенства

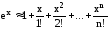(6.15)

определяется оценочной формулой , т.е. сумма отброшенных слагаемых в разложении функции е^х меньше величины при 0 < x < n +1.

Пример 1. Вычислить число е с точностью до 0,001.

Решение. Воспользуемся приближенным равенством (6.15), положив в нем х = 1, тогда . Из формулы оценки остатка ряда r_n(x) при х = 1 получим

.

Число членов частичной суммы ряда, обеспечивающее необходимую точность приближения, определим из неравенства r_n < 0,001 или < 0,001, т. е. n! n > 1000. Отсюда видно, что достаточно взять n = 6, так как 6!  6 = 720  7 + 4320 > 1000. Следовательно,

.

Слагаемые суммы необходимо вычислять с точностью до четвертого знака после запятой, чтобы при суммировании не получить погрешности, превышающей 0,001.

То есть

2,0000 + 0,5000 0,1667 0,0417 0,0083 0,0014 2,7181

Таким образом, е  2,7181.

Пример 2. Вычислить с точностью до 0,00001.

Решение. Положим в приближенном равенстве (6.15) , тогда получим

.

Выражение в правой части равенства представляет собой частичную сумму знакочередующегося ряда, удовлетворяющего признаку Лейбница. Поэтому допускаемая при отбрасывании членов ряда погрешность не превосходит модуля первого из отброшенных слагаемых.

Нетрудно видеть, что < 0,00001.

Следовательно, необходимая точность будет достигнута, если частичную сумму составить из пяти слагаемых, т. е.

.

Производя вычисления, окончательно получаем .

2. Приближенные вычисления определенных интегралов

Пример 3. Вычислить с точностью до 0,001.

Решение. Воспользуемся разложением функции в ряд Маклорена (см. Пример 2).

Тогда можно записать

Здесь учтено, что для достижения необходимой точности вычисления интеграла, достаточно ограничиться пятью слагаемыми, так как 0,0008 < 0,001.

111. Вычислить с точностью до 0,00001.

112. Вычислить с точностью до 0,00001.

113. Вычислить ln 1,04 с точностью до 0,0001.

114. Вычислить с точностью до 0,0001.

115. Вычислить ln 0,98 с точностью до 0,001.

116. Вычислить cos 18⁰ с точностью до 0,0001.

117. Вычислить sin 9⁰ с точностью до 0,0001.

118. Вычислить с точностью до 0.001.

119. Вычислить с точностью до 0,0001.

120. Вычислить с точностью до 0,001.

121. Вычислить с точностью до 0,0001.

ОГЛАВЛЕНИЕ

Глава I. ВВЕДЕНИЕ В АНАЛИЗ 2

Глава II. ПРЕДЕЛЫ 4

Глава III. ДИФФЕРЕНЦИРОВАНИЕ 17

§1. Производная функции ……………………………………………….17

§2. Дифференциал функции 29

§3. Исследование функций и построение графиков 32

§4. Функции нескольких переменных 48

§5. Экстремумы функции двух переменных 53

Глава IV. ИНТЕГРИРОВАНИЕ 59

§ 1. Первообразная и неопределенный интеграл 59

§ 2. Методы интегрирования 60

§ 3. Определенный интеграл 67

§ 4. Методы вычисления определенного интеграла 70

§ 5. Приближенное вычисление определенных интегралов 74

§ 6. Геометрические приложения определенного интеграла 79

§ 7. Несобственные интегралы 83

Глава V. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 86

§ 1. Основные понятия и определения 86

§ 2. Дифференциальные уравнения первого порядка……………….... 86

§ 3. Дифференциальные уравнения второго порядка 99

§ 4. Приложения дифференциальных уравнений 105

Глава VI. РЯДЫ 109

§ 1. Числовые ряды 109

§ 2. Знакопеременные ряды 118

§ 3. Функциональные ряды 121

§ 4. Степенные ряды 123

§ 5. Ряд Тейлора 128

§ 6. Применение степенных рядов к приближенным вычислениям 132

137