
Учебное пособие Теории вероятностей и математическая статистика
.pdf
2.55. Радиус круга R – случайная величина, распределённая по закону Релея:
|
|
|
|
r |
|
e |
r2 |
|
|
|
|
|
|
||
|
|
f (r) |
|
2 2 |
при r > 0. |
|
|||||||||
|
|
|
|
|
|||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
Найти закон распределения площади круга S. |
|
||||||||||||||
2.56. Непрерывная с.в. Х |
( |
) |
|
|
( 0). |
|
|||||||||
Найти математическое ожидание и дисперсию с.в. |
. |
||||||||||||||
2.57. Непрерывная с.в. Х распределена по закону: |
|
||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
cos x |
при x |
|
|
|
|
; |
|
, |
|
||||
|
|
|
|
|
|||||||||||
|
2 |
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
f (x) |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
0 |
|
|
|
|
; |
|
||||||||
при x |
|
|
|
|
|
. |
|
||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|||||
Найти числовые характеристики с.в. Y sin X .
Раздел III СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН
3.1 Двумерные распределения вероятностей
Совокупность двух (или более) случайных величин ( X ,Y ) ,
( X ,Y , Z,...), рассматриваемых совместно, называется системой двух (или более) случайных величин. Геометрически систему двух случайных величин можно интерпретировать как случайную точку ( X ,Y )
на плоскости хОу.
Закон распределения системы двух дискретных с.в. ( X ,Y )
pij P{X xi ,Y y j }, i 1, |
,n, |
j 1, |
,m в случае конечного числа |
||||
значений можно задать с помощью таблицы: |
|||||||
|
|
|
|
|
|
|
|
|
X\Y |
y1 |
|
y2 |
… |
|
|
|
x1 |
p11 |
|
p12 |
… |
p1m |
|
|
x2 |
p21 |
|
p22 |
… |
p2m |
|
|
… |
... |
|
… |
… |
… |
|
|
xn |
pn1 |
|
pn2 |
… |
pnm |
|
где вероятности pij подчиняются условию
∑∑
61
|
Функцией распределения ( |
) системы двух с.в. ( |
) назы- |
|||
вается вероятность совместного появления двух событий { |
} и |
|||||
{ |
}, т.е. ( ) |
{ |
} |
причём событие { |
|
|
} |
означает произведение событий { |
} { |
}. |
|
||
|
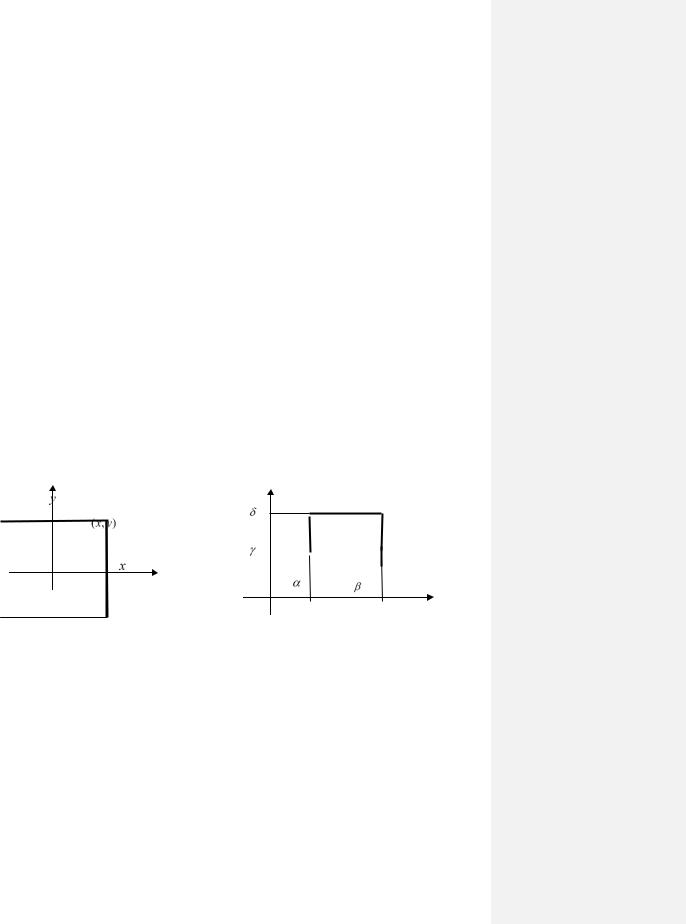
Геометрически F (x, y) означает вероятность попадания случай- |
|||||
ной точки ( X ,Y ) в квадрант с вершиной в точке (x,y), заштрихованный на рис. 3.1.
Вероятность попадания случайной точки (Х, Y) в прямоугольник S со сторонами, параллельными осям координат, включающий свою нижнюю и левую границы, но не включающий верхнюю и правую (рис. 3.2), выражается через функцию распределения формулой
P{(X ,Y ) S} F( , ) F( , ) F( , ) F( , ) .
Функция распределения F (x, y) обладает свойствами:
1) |
|
( ) |
|
|
|
|
2) |
( |
) – неубывающая функция х и у; |
||||
3) |
( |
) |
( |
) |
( |
) |
4)F( , ) 1;
5)F(x, ) F1 (x) FX (x), F( , y) F2 ( y) FY ( y), где F1 (x) и
F2 ( y) – функции распределения случайных величин X и Y .
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ОО |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
Рис. 3.2 |
|
x |
|||
|
|
|
|
||||||||
|
|
Рис. 3.1 |
|
|
|||||||
Значение F (x, y) в случае системы двух дискретных с.в. равно |
|||||||||||
сумме всех вероятностей pij , для которых xi |
x, y j |
y, т.е. |
|||||||||
F (x, y) pij .
xi x y j y
Одномерные законы распределения отдельных компонент дискретной системы с.в. выражаются через вероятности совместных значений рij формулами
62

pi P{X xi } pij , |
p j P{Y y j } pij , |
j |
i |
Плотность распределения вероятностей f(x,y) системы двух не-
прерывных случайных величин ( X ,Y ) выражается через функцию распределения формулой
f (x, y) |
2 F (x, y) |
|
(x, y). |
|
|||
x y |
Fxy |
||
|
|
|
Свойства плотности распределения:
1) f (x, y) 0;
2)условие нормировки: f (x, y)dx dy 1;
3) P{( X ,Y ) D} f (x, y) dx dy, где D – произвольная область;
D
xy
4)F (x, y) f (s,t)dsdt;
|
|
|
|
||
|
|
|
|
|
|
5) f (x, y)dy f1 (x) f X (x), |
f (x, y)dx f2 ( y) fY ( y) |
– |
|||
|
|
|
|
|
|
одномерные плотности распределения с.в. Х и Y. |
|
||||
Пример. Задана плотность распределения двумерного непре- |
|||||
рывного случайного вектора |
|
|
|||
|
2 |
y), |
0 x 1; |
5 y 5; |
|
f (x, y) C(x |
|
|
|||
0 |
|
|
в остальных случаях. |
|
|
Найти значение параметра С и плотность распределения составляющей у.
Решение. Запишем условие нормировки плотности распределения
C (x2 y)dxdy 1,
D
где замкнутая область  Вычисляя этот двойной интеграл, получаем: 10С/3 = 1, откуда С = 0,3. Плотность распределения составляющей y , согласно свойству 5), равна
Вычисляя этот двойной интеграл, получаем: 10С/3 = 1, откуда С = 0,3. Плотность распределения составляющей y , согласно свойству 5), равна
1
f2 ( y) 0,3 (x2 y)dx 0,1 0,3y
0
63

при  Аналогично получа-
Аналогично получа-
3x2 , x [0,1];
ется плотность распределения : f1 (x)
0, x [0,1].
Зависимость и независимость случайных величин.
СВ называются независимыми, если независимы события
{X x} и {Y y} для любых действительных х и у . Иными словами, необходимо и достаточно, чтобы функция распределения имела вид F(x, y) F1 (x)F2 ( y) . Отсюда следует, что аналогичное соотношение должно выполняться и для плотности вероятности:
f (x, y) f1 (x) f2 ( y) .
Для дискретных с.в. это соотношение запишется в виде
P{X xi ,Y y j } P{X xi } P{Y y j }
|
|
|
|
|
|
или pij pxi pyj |
(i 1, n; j 1, m) |
||||
3.2. Условные законы распределения
Пусть ( X ,Y ) – система двух дискретных с.в. Условным законом распределения с.в. Х при условии, что с.в. Y имеет определённое (фиксированное) значение yj,, называется совокупность вероятностей
P{X x /Y y |
} |
P{X xi ,Y y j } |
|
|
pij |
. |
|
|
|
||||||
i |
j |
|
P{Y y j } |
|
p j |
||
|
|
|
|
||||
Совокупность вероятностей p( y1 / xi ), p( y2 / xi ),..., p( ym / xi ) представ-
ляют собой условный закон распределения с.в. Y при условии Х = хi . Соответствующее равенство для событий имеет вид
P(B / A) P( AB) P( A)
Аналогично определяется условный закон распределения дискретной с.в. X при условии Y y j . При этом для условных вероятно-
стей выполняется условие нормировки
p( y j |
/ xi ) pij |
|
1 pij |
pxi |
1. |
|||
m |
m |
|
|
|
m |
|
|
|
j 1 |
j 1 pxi |
|
pxi j 1 |
|
pxi |
|
||
64

Условная плотность f ( y / x) непрерывной с.в. Y при условии X = x определяется равенством
f ( y / x) |
f (x, y) |
, |
f (x) 0. |
|
|||
|
f1 (x) |
1 |
|
|
|
||
Аналогично
f (x / y) |
f (x, y) |
, |
f |
|
( y) 0. |
|
2 |
||||
|
f2 ( y) |
|
|
||
|
|
|
|
||
Теорема умножения плотностей распределения:
f (x, y) f1 (x) f ( y / x) f2 ( y) f (x / y).
Случайные величины Х и Y называются независимыми, если условный закон распределения одной из них не зависит от того, какое значение примет другая случайная величина:
f (x / y) f1 (x) или |
f ( y / x) f2 ( y). |
Теорема умножения для плотности распределения независимых с.в. записывается в виде f (x, y) f1 (x) f2 ( y) и аналогично для
функции распределения F(x, y) F1 (x) F2 ( y).
В случае дискретных с.в. (X,Y) необходимым и достаточным условием их независимости является равенство
pij pi p j .
3.3 Числовые характеристики двумерного случайного вектора. Корреляционный момент
Начальным моментом порядка k+s случайного вектора (X,Y)
называется действительное число k ,s , определяемое формулой
|
|
|
|
|
xik ysj pij , |
если ( X ,Y ) дискретная с.в., |
||||||
|
|
|
|
|
i |
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k ,s M ( X kY s ) |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
x |
k |
y |
s |
f (x, y)dx dy, если ( X ,Y ) непрерывная с.в. |
|||
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||
В частности, |
k ,0 |
M ( X k ), |
0,s |
M (Y s ) – соответствующие моменты |
||||||||
|
|
|
|
|
|
|
|
|
|
|
||
отдельных компонент.
Вектор с неслучайными координатами (mX , mY ) ( 1,0 , 0,1 )
называется математическим ожиданием случайного вектора (X,Y)
или центром рассеивания.
65

Центральным моментом порядка k+s случайного вектора (X,Y)
называется действительное число k ,s , определяемое формулой
|
|
|
(xi mX )k ( y j |
mY )s pij , |
( X ,Y ) дискретная с.в. |
||||
|
|
|
i |
j |
|
|
|
|
|
k ,s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
(x mX ) |
k |
( y mY ) |
s |
f (x, y)dx dy, ( X ,Y ) непрерывная с.в. |
||
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||
В частности, |
2,0 |
DX , 0,2 DY . |
|
|
|||||
Для характеристики связи между величинами X и Y служит ко-
вариация, или корреляционный момент KXY , который определяется по формуле
cov(X ,Y ) KXY 1,1 M[( X mX )(Y m)] M[XY ] mX mY . (3.1)
Очевидно, что при Y X
KXX D(X ) M (X 2 ) [M ( X )]2 .
Для дискретных с.в.
KXY i, j
формула (3.1) запишется в виде
|
|
xi pi |
|
y j |
|
xi y j pij |
|
|
p j . |
||
|
|
i |
|
j |
|
Случайные величины Х и Y называются некоррелированными, если KXY 0. Это условие в силу (3.1) выполняется тогда и только тогда,
когда M ( XY ) M (X ) M (Y ) mX mY .
Для с.в. Х и Y с конечными дисперсиями
D(X Y ) D(X ) D(Y ) 2KXY ,
или в общем виде
D(aX bY c) a2 D(X ) b2 D(Y ) 2abK |
XY |
|||
|
|
|
||
Нормированный корреляционный момент XY |
K XY |
|
называется |
|
X |
Y |
|
||
|
|
|
||
коэффициентом корреляции двух с.в. X и Y, где X и |
Y – средне- |
|||
квадратические отклонения случайных величин X и Y.
Свойства коэффициента корреляции
1.1 XY 1.
2.Если XY 1, то с.в. X и Y связаны линейной зависимостью
YaX b.
3.Если XY 0, то такие с.в. называются некоррелированными.
Из независимости с.в. X и Y вытекает их некоррелированность (обратное, вообще говоря, неверно).
66

Для некоррелированных с.в. X и Y
D( X Y ) D( X ) D(Y ), |
D( X Y ) D( X ) D(Y ), |
|
|
|
|
||||||||||
D(aX bY c) a2 D( X ) b2 D(Y ). |
|
|
|
|
|
|
|
|
|||||||
Если с.в. Х и Y связаны линейной зависимостью – |
|
|
|
|
|||||||||||
Y aX b, a 0, то |
|
XY |
|
1. Справедливо и обратное: если |
|
XY |
|
1, |
|||||||
|
|
|
|
||||||||||||
то с.в. Х и Y связаны линейной зависимостью. |
|
|
|
|
|
|
|
|
|||||||
Пусть ( X ,Y ) – система дискретных с.в. Условным математи- |
|||||||||||||||
ческим ожиданием с.в. Х при условии, что Y принимает одно из своих |
|||||||||||||||
возможных значений уj, называется величина |
pij , |
|
|
|
|
||||||||||
M ( X /Y y j ) M ( X / y j ) xi p(xi / y j ) xi |
|
|
|
|
|||||||||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
i |
p j |
|
|
|
|
||||
где p(xi / y j ) P{X xi /Y y j } |
– условная вероятность, опреде- |
||||||||||||||
лённая выше. |
|
|
|
|
|
|
|
|
|
|
|
||||
Аналогично |
|
|
|
|
pij . |
|
|
|
|
||||||
M (Y / X xi ) M (Y / xi ) y j p( y j / xi ) y j |
|
|
|
|
|
||||||||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
j |
|
pi |
|
|
|
|
|||
Функция |
|
|
|
|
|
|
|
|
|
|
|
||||
y H (x) M (Y / X x) , |
|
|
|
|
(3.2) |
||||||||||
заданная на множестве {x1, x2 ,...} значений с.в. Х, называется регрессией величины Y на X, а само соотношение (3.2) рассматривается как
уравнение регрессии Y на Х.
Пусть теперь ( X ,Y ) – система непрерывных с.в. В этом случае
условное математическое ожидание с.в. Y при условии Х = х опреде-
ляется равенством
M (Y / x) y f ( y / x)dy.
Аналогично
M ( X / y) x f (x / y)dx.
Пример
Задана таблица распределения дискретной двумерной с.в.
X\Y |
1 |
2 |
|
3 |
1 |
0,16 |
0,12 |
|
0,08 |
2 |
0,28 |
0,11 |
|
0,25 |
|
|
|
67 |
|

1.Найти законы распределения составляющих Х и Y, их математические ожидания и дисперсии.
2.Найти функцию распределения системы с.в. (Х, Y).
3.Установить, зависимы или нет компоненты Х и Y.
4.Вычислить корреляционный момент и коэффициент корреляции случайного вектора ( X ,Y ).
5.Получить уравнения регрессии Н(x) величины Y на Х и G(y) величины Х на Y.
6.Вычислить вероятность P{X Y}.
Решение
1. С.в. Х принимает два значения: х1 = 1 и х2 = 2. Вероятности этих значений получатся, если сложить соответствующие вероятнос-
ти по строкам: P( X 1) p1 |
p11 p12 p13 |
0,16 0,12 0,08 0,36, |
|||||||||
P( X 2) p2 |
0,28 0,11 0,25 0,64. |
|
|
|
|||||||
Аналогично получается безусловный закон распределения ком- |
|||||||||||
поненты Y. |
|
|
|
|
|
|
|
|
|
||
Таким образом, с.в. |
Х и Y имеют следующие частные распре- |
||||||||||
деления вероятностей: |
|
|
|
|
|
|
|
||||
|
|
1 |
2 |
|
|
|
1 |
2 |
|
3 |
|
X |
|
0,36 |
0,64 |
, |
Y |
|
0,44 |
0,23 |
0,33 |
. |
|
|
|
|
|
|
|
||||||
Математические ожидания и дисперсии вычисляются по опреде- |
|||||||||||
лению: |
|
|
|
|
|
|
|
|
|
|
|
M ( X ) mX 1 0,36 2 0,64 1,64; |
|
|
|
||||||||
D( X ) 12 |
0,36 22 |
0,64 1,642 |
0,2304; |
X 0,48. |
|||||||
Аналогично получаем |
|
|
|
|
|
|
|||||
mY |
1,89; |
D(Y ) 0,7579; |
Y 0,8706. |
|
|
||||||
2. Значения функции распределения F (x, y) |
вычисляются в со- |
||||||||||
ответствии с определением:
. F (x, y) pij
xi x y j y
Так, если x 1, то при любом значении у F(x, y) 0, и аналогично при y 1. Если 1 x 2 и 1 y 2, то F(x, y) P{X 1,Y 1} 0,16 ;
если 1 x 2 и 2 y 3, то
F(x, y) P{X 1,Y 1} P{X 1,Y 2} 0,16 0,12 0,28 и т.д.
68

В итоге функция распределения имеет вид
|
|
|
|
|
|
|
при |
y 1 |
1 y 2 |
2 y 3 |
3 y |
||
|
|
|
|
|
|
|
x 1 |
0 |
0 |
0 |
0 |
||
|
||||||
F (x, y) |
1 x 2 |
0 |
0,16 |
0,28 |
0,36 |
|
|
|
|
|
|
|
|
2 x |
0 |
0,44 |
0,67 |
1 |
||
|
||||||
|
|
|
|
|
|
3. Условие независимости с.в. Х и Y в данном случае имеет вид pij pi p j для любых i и j. Проверим, например, при i = 1 и j = 2. p12 0,12 0,36 0, 23 p1 p 2 .Следовательно, с.в. Х и Y зависимы.
4. Корреляционный момент равен:
M ( XY ) 1 1 0,16 1 2 0,12 1 3 0,08 2 1 0,28
2 2 0,11 2 3 0,25 3,14;
KXY M ( XY ) mX mY 3,14 1,64 1,89 0,0404.
Коэффициент корреляции ρ вычисляется по определению:
|
KXY |
0,0967. |
||
X |
Y |
|||
|
|
|||
Поскольку KXY 0, величины Х и Y являются коррелированными и, следовательно, зависимыми, хотя эта зависимость и слабая (ρ близко к нулю).
5. Для того чтобы найти функцию H (x) M (Y / X x), которая определена в двух точках: х = 1 и х = 2, найдём условные распределения величины Y при заданных значениях х
P(Y 1/ X 1) |
p11 |
|
|
0,16 |
0, 4444; |
|
|
||
|
p1 |
0,36 |
|
|
|||||
|
|
|
|
|
|
|
|||
аналогично |
|
|
|
|
|
|
|
|
|
P(Y 2 / X 1) |
|
p12 |
0,3333; |
P(Y 3/ X 1) |
p13 |
0, 2222. |
|||
|
|
|
|
||||||
|
|
p1 |
|
|
|
|
p1 |
||
Используя полученное условное распределение вероятностей, нахо-
дим H (1) M (Y / X 1) 1 0,4444 2 0,3333 3 0,2222 1,7777.
Подобным образом считается всё остальное:
P(Y 1/ X 2) 0, 4375; P(Y 2 / X 2) 0,1719;
P(Y 3/ X 2) 0,3906; |
H (2) 1,9532; |
69

Результаты вычислений удобно представить в виде таблицы:
X |
|
Y |
1 |
2 |
3 |
pi• |
pX /Y 1 |
pX /Y 2 |
pX /Y 3 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
0,16 |
0,12 |
0,08 |
0,36 |
0,364 |
0,522 |
0,242 |
2 |
|
|
0,28 |
0,11 |
0,25 |
0,64 |
0,636 |
0,478 |
0,758 |
p•j |
|
0,44 |
0,23 |
0,33 |
1 |
1,636 |
1,478 |
1,757 |
|
pY / X 1 |
|
0,444 |
0,333 |
0,222 |
1,777 |
|
G( y) |
|
|
pY / X 2 |
|
0,437 |
0,172 |
0,391 |
1,953 |
H (x) |
|
||
Кроме исходных данных (первые две строки и три столбца) она содержит частные распределения с.в. Х и Y. Эти величины получаются путём суммирования исходных величин по строкам и по столбцам. В последней клетке на пересечении столбца pi и строки
p j стоит единица – сумма всех вероятностей, как соответствующих
2 |
3 |
2 |
3 |
|
частных pi , |
p j |
, так и данных исходной таблицы pij |
1. |
|
i 1 |
j 1 |
i 1 j 1 |
|
|
Условные вероятности получаются путём деления элементов строки (столбца) на соответствующую частную вероятность. Наконец, выделенные числа дают значения регрессий.
6. Искомая вероятность определяется по общей формуле (68), где область G – часть плоскости, в которой выполняется неравенство
x y . Тогда получим
2 |
3 |
|
P{X Y} pij |
p11 p21 p22 0,16 0,28 0,11 0,55. |
|
i 1 |
j 1 |
|
( xi y j ) |
|
|
Задачи
3.1. По мишени производится один выстрел. Вероятность попадания равна 0,75. Рассматриваются две с.в.: Х – число попаданий; Y – число промахов. Составить таблицу совместного распределения вероятностей с.в. Х и Y. Построить функцию распределения F (x, y) системы (Х, Y).
3.2. Двумерное распределение пары случайных целочисленных величин и задаётся с помощью таблицы:
70
