Учебное пособие Теории вероятностей и математическая статистика

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Балтийский государственный технический университет "ВОЕНМЕХ" им. Д.Ф. Устинова

Предмет:

Теория вероятностей и математическая статистика

Файл:

xf (x)dx xe xdx

xf (x)dx xe xdx

.pdf

Скачиваний:

226

Добавлен:

26.03.2015

Размер:

2.37 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 136 7 8 9 10 11 12 13 > Следующая >>>

			a	x	dt
если a x b,		F (x)		0 dt
					b a
				a

	a	b	dt	x
x b	F (x) 0 dt			0 dt 1.
			b a
		a		b

x a ; при b a

	0,		x a,

x a
Таким образом, F (x)		,	a x b,
Таким образом, F (x)		,	a x b,
b a			x b.
	1,		x b.

Графики функций f(x) и F(x) приведены на рис. 13. При этом значения плотности вероятности в точках а и b никак не фиксируются, т.е. можно положить например, f (a) f (b) 0,или

1
f (a) f (b) b a	и даже как-нибудь иначе, ибо эти значения	в

отдельных точках никак не сказываются на функции распределения F(x). Поэтому можно говорить о равномерном распределении на отрезке [a, b].

Равномерное распределение обычно обозначают следующим об-

разом:	X R(a,b).
Числовые характеристики распределения
	M ( X )	a b	, D( X )	(b a)2
					.
		2		12

Упражнение. Вычислить асимметрию и эксцесс для равномер-
ного распределения.
	Ответ:		AX 0, EX	1,2.
Примеры с.в., имеющих равномерное распределение						( )
1)	Х – координата х точки, которая ставится наугад на отрезке
[a, b];	2) абсолютная погрешность округления при снятии показания

измерительного прибора с определённой ценой деления шкалы; 3) случайное время прихода пассажира на остановку транспорта при известном или неизвестном интервале движения транспорта.

Задачи

2.27. Поезда метро ходят с интервалом 5 мин. Найти вероятность того, что пассажир, вышедший на платформу в случайный момент времени, будет ожидать поезд не менее 3 минут.

2.28.Некто, подходя к остановке автобуса, в течение 50 секунд видит, как примерно один раз из 12 у него «из-под носа» уходит автобус. Определить средний интервал движения автобуса.

2.29.Длина комнаты измеряется с помощью рулетки с грубыми делениями, расстояние между которыми составляет 10 см. Округление производится до ближайшего деления; с.в. Х – ошибка измерения.

Найти и построить графики плотности вероятности f(x), функции

распределения F(x); найти M (X ), D(X ), ( X ).

2.30. Случайная величина Х распределена равномерно в некотором интервале. Построить графики её функции распределения F (x) и

плотности вероятности f (x), если M (X ) 2,

D( X ) 0,75.

2.31. Вычислить математическое ожидание и дисперсию с.в. Х , равномерно распределённой в некотором интервале, если известно, что:

1) P(0 X 1) 2 /	3,	P(1	X 2)	1/ 6;
2) P(1 X 2) 1/	6,	P(3	X 4)	5 /12.

2.32. На стороне АВ=1 равностороннего треугольника АВС выбирается точка М. Найти математическое ожидание и дисперсию площади треугольника АМС.

2) Экспоненциальное (показательное) распределение E( )

Плотность вероятности показательного распределения непрерывной с.в. Х с параметром λ > 0 задаётся функцией

	x
f (x) e	x	, x 0,
f (x) e		, x 0,
0,		x 0.
Соответствующая ей функция распределения определяется по
формуле
			x	, x 0,
F (x) 1- e				, x 0,
		0,		x 0.
Запись X	E( ) означает, что с.в. Х распределена по экспонен-

циальному закону с параметром λ.

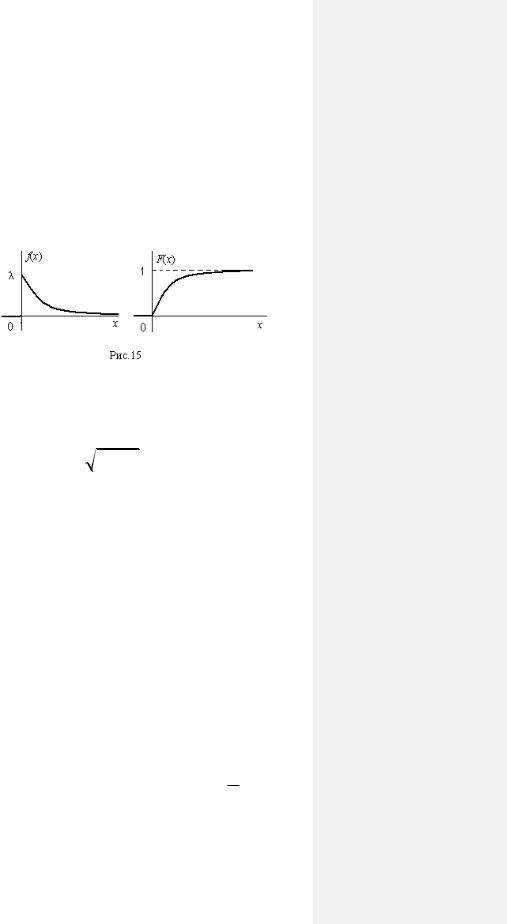
Графики функций f (x) и F (x) приведены на рис. 15. Вероятность с.в. Х попадания в интервал ( , ) определяется формулой

P( X ) F( ) F( ) e e .

Вычислим числовые характеристики показательного распределения. При вычислении интегралов удобно использовать приём дифференцирования интеграла по параметру:

В результате получим

Вычисляя аналогично интеграл для дисперсии, получим

		1	2	1	1
D( X ) M ( X 2 ) m2	x2e x dx					.

x		2	2	2	2

	0
При этом значения	mx и среднеквадратичного отклонения x для

показательного закона совпадают: x D( X ) 1/ .

3) Показательный закон надёжности.

Экспоненциальное распределение часто используется для характеристики надёжности приборов и технических систем.

Пусть элемент – это техническое устройство, работающее самостоятельно или в блоке с другими (например, блок ПК, чип, узел велосипеда, автомобиля и т.д.). Тогда длительность безотказной работы можно рассматривать как непрерывную с.в. Т. Функция ( ) {

} определяет вероятность отказа элемента за время t. Вероятность безотказной работы элемента за то же время t есть вероятность противоположного события и равна

R(t) P(T t) 1 F(t) e t ,

(2.18)

где λ – интенсивность отказов, т.е. число отказов в единицу времени.

В этих случаях вместо λ удобно использовать параметр 1 . Тогда имеем

	1		t
				t 0,
		e	,

f (t)
	0,			t 0,

и M (T ) – среднее время безотказной работы систем.

Пример. Пусть плотность вероятности работы элемента задана функцией

f (t) 0,05e 0,05 t ,

где - интенсивность отказов, t – время работы (в сутках), t 0. Вычислить вероятность того, что прибор проработает безотказно в течение 30 суток.

Согласно формуле (2.18), эта вероятность равна

R(30) e 0,05 30 e 1,5 0, 22.

И вообще, если - среднее время работы прибора, то в конце этого времени надёжность работы прибора составляет лишь e 1 0,37, т.е. очень малую величину. Следовательно, для надёжной работы необходимо либо раньше менять такой узел, либо производить профилактический ремонт («подтягивать гайки»).

Задачи

2.33. X E( ) . Найти вероятность попадания с.в. Х в интервал

(a,b), где	.
2.34. Для случайной величины		E( ) вычислить

PM ( ) 3D( ) .

2.35.Время Т выхода из строя радиостанции подчинено показательному закону распределения с плотностью

	0,	t 0,
f (t)
0,2 e 0,2t ,t 0.

Найти функцию распределения F (t) ; математическое ожидание и дисперсию с.в. Т; вероятность того, что радиостанция сохранит работоспособность от 1 до 5 часов работы.

2.36. Какое событие для случайной величины X E( ) более вероятно: ( X M ( X )) или X M ( X ) ?

2.37. Пусть случайная величина ξ имеет показательное распределение с параметром . Найти плотности распределения следующих

					г) e .
случайных величин: a) ;			б) 2 ;	в) min( , 2 );	г) e .

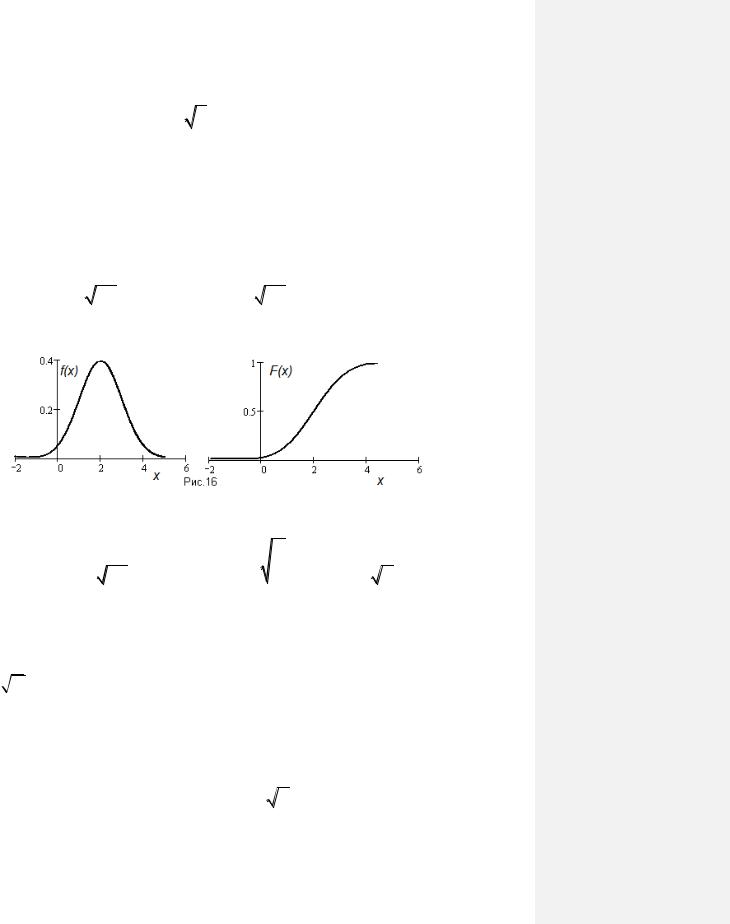
4) Нормальное (гауссово) распределение N (a, )

Непрерывная случайная величина Х имеет нормальное распределение (распределена по закону Гаусса), если её плотность вероятности f(x) и функция распределения F(x) имеют вид

	1		( x a)2		1	x	(t a)2
f (x)		e-		F (x)		e-
			2 2 ,				2 2 dt.	(2.19)
			2 2 ,				2 2 dt.	(2.19)
	2				2

Графики этих функций представлены на рис. 16.

Математическое ожидание нормально распределённой с.в. определяется интегралом

( x a)2

M ( X )

xe-

ze z2 dz

e z2 dz.

2 2

Здесь использована очевидная замена

z (x a) / ;

x z a;

dx dz.

Первый интеграл равен нулю как интеграл от нечётной функции в симметричных пределах, а второй есть интеграл Пуассона и равен

. Отсюда, ( ) . Следовательно, параметр a имеет смысл математического ожидания нормально распределённой с.в. На графике гауссовой кривой он фиксирует положение максимума.

Дисперсия нормального распределения равна

	( x a)2		2	2
D( X ) (x a)2 e		dx			z2e z2 dz
	2 2
	2 2



			55


		2		2		2		2
			ze z		e z		dz		(0 ) 2 .
			ze z		e z		dz		(0 ) 2 .



Следовательно, среднее квадратическое отклонение равно

( X )	D( X ) . Оно определяется вторым параметром нормаль-

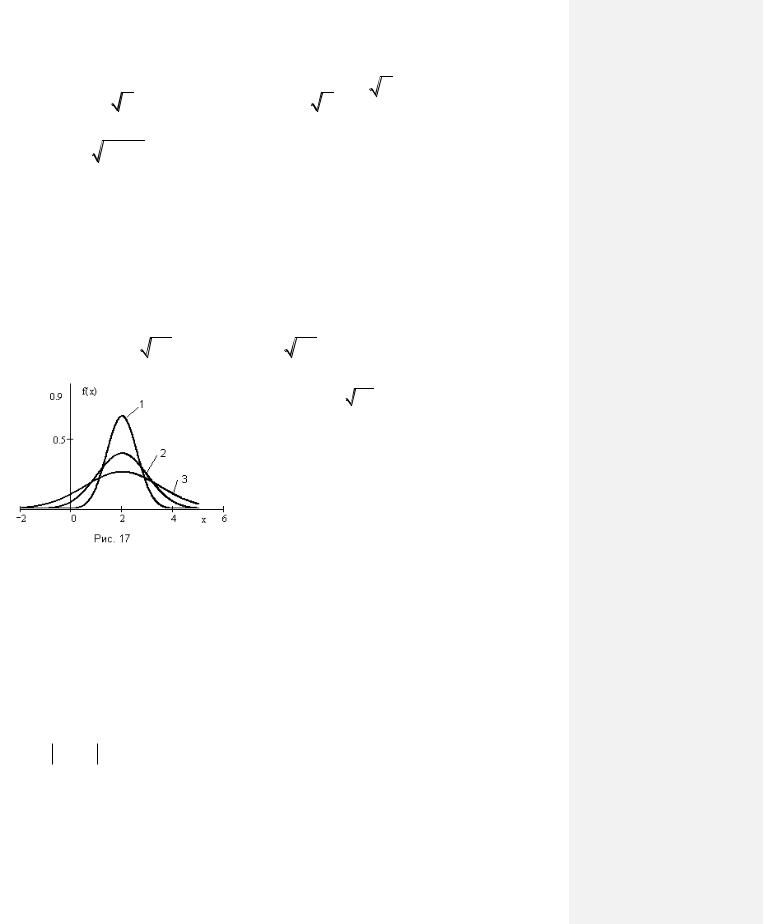
ного распределения. Значение параметра σ характеризует величину максимума гауссовой кривой и отклонение случайной величины от среднего значения, что видно из рис. 17. Для изображённых кривых:

1 – 0,6 , 2 – 1, 3 – 1,5.

В частности, при а = 0 и σ = 1 распределение называют стандарт-

ным нормальным ( ( ))

Оно определяется функциями

			1			x2
		(x) (x)	1
f	0			e	2 ,

			2

	1		x	e	t2					1
F (x)	1				2		dt			1		0	(x),
F (x)					2		dt						(x),
0		2							2
		2							2

						1 x					t2
где	0 (x)					2		e			2 dt - введённая уже

					0
					0

ранее функция Лапласа.

Для нормального распределения с параметрами а и σ эти функции равны соответственно

	x a
	f (x)			,

Вероятность попадания в интервал ( , ) равна

	1	x a
F (x)		0	.
	2

	a	0	a
P( X ) F ( ) F ( ) 0		0		,

откуда легко получается формула


P(	X a	) 2 0	.

В частности, при 3 получаем правило трёх сигм:

P( X a 3 ) 2 0 (3) 0,9973, т.е. нормально распределённая с.в.

Х с дисперсией σ2 практически не отклоняется от своего среднего значения больше, чем на 3σ (99,73 % значений с.в. попадает в интервал a 3 ).

Задачи

2.38.Что произойдёт с графиком функции распределения с.в. Х, если: а) к Х прибавить число 3; б) умножить Х на число 3?

2.39.Пусть с.в. X N (a, ). Известно, что P( X 2) 0,5;

P( X 3) 0,975. Вычислить P(1 X 3) и записать плотность распределения вероятности.

2.40. Деталь считается нормальной, если отклонение её размера от проектного не превышает 0,7 мм. Считая, что с.в. X N(a; 0,4 мм), найти, сколько годных деталей будет в среднем из 100 выбранных наугад.

2.41.Случайные ошибки измерения подчинены нормальному закону со средним квадратическим отклонением 20 мм и математическим ожиданием 0. Определить вероятность того, что из трёх независимых измерений ошибка хотя бы одного из них не превысит по абсолютной величине 4 мм.

2.42.Какую ширину должен иметь интервал допустимых отклонений размеров деталей от расчётных (со средним квадратическим отклонением 5 мк), чтобы с вероятностью не более 0,0027 отклонения размеров изготовленных деталей от расчётных выходили за пределы допустимых значений?

2.43.Химический завод изготовляет серную кислоту номинальной плотности 1,84 г/см3. В результате статистических испытаний обнаружено, что практически 99,9 % всех выпускаемых реактивов имеют плотность в интервале (1,82; 1,86). Найти вероятность того, что кис-

лота удовлетворяет стандарту, если для этого достаточно, чтобы её плотность не отклонялась от номинала более чем на 0,01 г/см3 .

2.44.Не пользуясь таблицами, решить, какая из вероятностей

P(	3)	и P(	3) больше, если:	a)	N(0,2), N(0,3);
P(	3)	и P(	3) больше, если:	a)	N(0,2), N(0,3);

б) N(0,2), N(1,2)?

2.45.Известно, что нормально распределённая с.в. Х удовлетворяет условию P( X M ( X ) 1) 0,3. Вычислить P( X M ( X ) 2).

2.46.С.в. Х распределена равномерно на интервале (а, b). Найти вероятность того, что в результате опыта она отклонится от своего математического ожидания больше чем на 3σх.

2.47. С. в. Х подчинена нормальному закону X N (0, X ) . Вероят-

ность попадания этой с.в. в интервал ( ) равна 0,5. Найти σХ и записать плотность вероятности нормального закона этой величины.

2.48.Производится стрельба тремя независимыми выстрелами по цели, имеющей вид полосы (мост, автострада, взлётно-посадочная полоса). Ширина полосы 20 м. Прицеливание производится по средней линии полосы; систематическая ошибка отсутствует; среднее квадратическое отклонение точки попадания в направлении, перпендикулярном полосе, 16 м. Найти вероятность р попадания в полосу при одном выстреле, а также вероятности следующих событий при трёх выстрелах: А – хотя бы одно попадание в полосу; В – не менее двух попаданий в полосу; С – один снаряд попадёт в полосу, один ляжет с недолётом и один с перелётом.

2.49.Завод изготавливает шарики для подшипников. Номинальный диаметр шарика а = 5 мм; фактический же диаметр можно рассматривать как нормально распределённую с.в. с математическим ожиданием а и среднеквадратическим отклонением σ = 0,05 мм. При контроле бракуются все шарики, диаметр которых отличается от номинального более чем на 0,1 мм. Какой процент шариков в среднем отбраковывается?

2.50.В условиях предыдущей задачи предположим, что σ не задано, зато известно, что в среднем отбраковывается 6 % шариков. Какова вероятность того, что диаметр наугад выбранного шарика будет заключён в пределах от 4,98 до 5,02?

2.4. Функции непрерывной случайной величины

Решим следующую задачу. Имеется непрерывная с.в. ξ, определённая на интервале ( ) с плотностью вероятности f (x), а с.в. η связана с.в. ξ функциональной зависимостью

( ).

Найти закон распределения и числовые характеристики с.в. η. Рассмотрим сперва случай, когда функция φ(ξ) строго монотон-

на, непрерывна и дифференцируема в интервале (а,b). Тогда существует функция ψ(y) = x, обратная функции φ(x) = y. Функция распределения G(y) с.в. η определяется следующим образом:

( y)

G( y) P{ y} P{ ( y)} f (x)dx .

Дифференцируя полученное выражение по y , находим плотность распределения с.в. η:

	dG		d ( y)
g( y)		f [ ( y)]		f [ ( y)]	( y)	.	(2.9)
g( y)	dy	f [ ( y)]	dy	f [ ( y)]	( y)	.	(2.9)
	dy		dy

Модуль ( y) ставится на тот случай, если функция φ(х) на участке

(a,b) монотонно убывает.

Если функция y = φ(x) немонотонна на (a,b), то для нахождения g(y) следует разбить интервал на k участков монотонности, найти обратную функцию на каждом из них. В результате функция плотности вероятности принимает вид

g( y) f [ i ( y)] i ( y) .

i 1

Числовые характеристики с.в. η находятся по формулам

M ( ) M ( ) (x) f (x)dx,

D( ) D ( ) [ (x) M ( )]2 f (x)dx.

Пример. Случайная величина ξ имеет равномерное распределение на отрезке [2, 4]. Найти математическое ожидание площади правильного треугольника со стороной ξ.

Решение. Согласно формулам равномерного распределения для плотности вероятности и функции распределения имеем

			1			0,	x 2,
			1	, x [2;4],
					x 2
					x 2
f (x)			2		F (x)		, 2 x 4,
f (x)			2		F (x)	2	, 2 x 4,
			0, x [2;4];			2
			0, x [2;4];			1,	x 4.

Искомая площадь связана со случайной величиной ξ								формулой

	3	2	и является также непрерывной величиной.					Для с.в. η про-
	4	2	и является также непрерывной величиной.					Для с.в. η про-
	4

ще всего вычислить функцию распределения G(y):

G( y)

[т.к.

					4x				2
	3				4x		2 x		2	x
P( y) P		2 y	P	2		P

									4 3
	4				3		4	3	4 3


		2		x		2		x			x
0] P	0				F				F (0)			1.
		4				4				4
			3				3				3
			3				3				3
						59

Определим пределы изменения y:

[2;4] y [ 3;4

3] , сле-

4 3

довательно, искомая функция распределения равна

, y [

3;4

3],

G( y)

1, 3

y 4 3,

g( y) G ( y)

3 y

4 3

y [

3;4

3].

y 4

С помощью последней вычислим математическое ожидание

28 3

M ( y)

2 4 3 x

Задачи

2.51. Для случайной величины

(

) вычислить M 3 5 .

2.52. Найти плотность вероятности случайной величины

построить её график, если случайная величина

распределена рав-

номерно в интервале: а) (0,250; 0,375);

б) (0; 0,5).

У к а з а н и е. Функция

хотя и не монотонна в обычном смысле слова (при

скачком возрастает от

до +

), но обратная функция однозначна, значит, задача может

быть решена так, как она решается для монотонных функций, то есть с помощью формулы (2.9), которая в данном случае запишется в виде:

( ) ( )

при тех значениях , которые могут быть обратными заданной совокупности возможных значений х.

2.53.			Случайная величина Х распределена равномерно в интервале
		,
		,	. Найти законы распределения случайных величин:
	2		2
а) Y sin X ; б) Y cos X ; в) Y					sin X			.
а) Y sin X ; б) Y cos X ; в) Y					sin X			.
2.54. Плотность распределения с.в. Х имеет вид
						0;
			cos x, x			0;			,
							2
			f (x)
			0,
			0,	x 0;					.
							2
							2

Найти: а) плотность распределения с.в. Y = X2; б) числовые характеристики M (Y) и D (Y).

<<< < Предыдущая 1 2 3 4 56 / 136 7 8 9 10 11 12 13 > Следующая >>>

Соседние файлы в предмете Теория вероятностей и математическая статистика