
Учебное пособие Теории вероятностей и математическая статистика
.pdf
p |
ak |
e a . |
(2.7) |
|
|||
k |
k ! |
|
|
|
|
|
Величина а называется параметром распределения Пуассона. Вычислим числовые характеристики, используя производящую
функцию.
|
a |
m |
|
|
(az) |
m |
|
||
(z) |
|
|
e a zm e a |
|
e aeaz ea( z 1) . |
||||
m! |
m! |
||||||||
m 0 |
|
m 0 |
|
||||||
|
a( z 1) |
|
a; |
|
|
||||
(z) ae |
|
|
|
|
, mx (1) |
|
|
||
(z) a2ea( z 1) , 2 (1) (1) a2 a,
Dx 2 mx2 a2 a a2 a.
Таким образом, в распределении Пуассона математическое ожидание и дисперсия равны одному и тому же значению
M ( X ) D( X ) a.
При некоторых условиях распределение Пуассона является предельным для биномиального (см. вывод формулы (1.18))
Задачи
2.1. Задан ряд распределения дискретной с.в.:
X |
-1 |
0 |
2 |
4 |
P |
0,1 |
0,3 |
0,5 |
0,1 |
Построить многоугольник распределения. Найти функцию распределения F(x) и построить её график. Вычислить числовые харак-
теристики с.в. Х.
2.2. Известно, что с.в. Х принимает значения -1; 0; 1, М(Х) = 0,1, D(X) = 0,9. Найти вероятности, с которыми принимаются значения Х.
2.3.Два спортсмена делают по одному броску мяча в корзину. Вероятность попадания в неё первым спортсменом равна 0,5; вторым – 0,4. Найти среднее число попаданий в корзину.
2.4.Стрелку выдано 4 патрона. Он производит выстрелы по мишени до первого попадания или пока не израсходует все патроны. Вероятность попадания в мишень при первом выстреле 0,4; при втором – 0,7; при третьем – 0,6; при четвёртом – 0,5. Случайная величина Х – число израсходованных патронов. Найти закон её распределения и числовые характеристики с.в.
2.5.По заданной функции распределения с.в. Х
41

0, |
x 1, |
|
|
|
|
|
||
|
0,25, |
1 x 2, |
|
|
|
|
||
|
|
|
|
|
||||
F (x) |
0,75, |
2 x 3, |
вычислить М(Х) и D(X). |
|||||
|
|
|
|
|
||||
|
1, |
|
x 3 |
|
|
|
|
|
|
|
|
|
|
|
|||
2.6. Дискретная с.в. Х задана рядом распределения |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
xi |
-2 |
1 |
2 |
3 |
|
|
|
|
pi |
0,08 |
0,40 |
0,32 |
0,2 |
|
Найти: а) функцию распределения F(x); б) вероятности событий A {X 2}, B {1 X 3}, C {1 X 3}; в) построить график функции F(x).
2.7.В команде 16 спортсменов, из которых 6 перворазрядников. Наудачу выбирают двух спортсменов. Построить ряд распределения и функцию распределения числа перворазрядников среди выбранных.
2.8.Вероятности сдать экзамен по математике на отлично для каждо-
го из троих студентов равны 0,9, 0,8 и 0,7 соответственно. Пусть Х
– общее число полученных ими отличных оценок. Вычислить М(Х) и
D(X).
2.9.Артиллерийское орудие производит три выстрела по цели с вероятностями попадания 0,6; 0,7; 0,8 соответственно. Составить закон распределения с.в. Х – числа попаданий орудия в цель. Вычислить числовые характеристики этой случайной величины.
2.10.Из колоды карт (32 листа) наудачу извлекают три. Составить закон распределения числа тузов среди извлечённых карт.
2.11.Независимо испытываются на надёжность 3 прибора. Вероятности выхода из строя каждого прибора одинаковы и равны 0,6. Найти М(Х) и σ(Х), где с.в. Х – число вышедших из строя приборов.
2.12.Найти математическое ожидание суммы числа очков, которые выпадают при бросании двух игральных костей.
2.13.Вероятность того, что студент сдаст экзамен на «5», равна 0,2, на «4» – 0,4. Определить вероятности получения им оценок «3» и «2», если известно, что М(Х) = 3,7, где дискретная с.в. Х – оценка, полученная студентом на экзамене.
2.14.На новогодней ёлке погасла гирлянда, состоящая из 15 лампочек. Для отыскания перегоревшей лампочки проверяются по очереди все лампочки гирлянды. 1. Сколько в среднем придётся проверить
42

лампочек, чтобы обнаружить перегоревшую? 2. Какова вероятность того, что для обнаружения перегоревшей лампочки придётся проверить не менее половины всех лампочек?
2.15. Рабочий обслуживает три автоматические линии, действующие независимо друг от друга. Вероятности того, что в течение смены эти линии потребуют вмешательства рабочего, равны соответственно 0,30; 0,35; 0,40. Найти математическое ожидание и дисперсию числа линий, которые потребуют вмешательства рабочего в течение смены.
Решение. Пусть X1, X2 , X3 – случайные величины, принимающие
значения 1 и 0 в зависимости от того, потребует или не потребует вмешательства рабочего соответствующая автоматическая линия; тогда распределение вероятностей для них имеет вид
1 |
0 |
|
|
1 |
0 |
|
1 |
0 |
||||
X1 |
0,30 |
0,70 |
|
; X |
2 |
|
0,65 |
|
; X3 |
|
0,60 |
. |
|
|
|
|
0,35 |
|
|
0,40 |
|
||||
|
|
|
|
|
|
|
|
|
||||
Каждую из этих с.в. можно рассматривать как число наступлений события А в одном испытании. Такое распределение называется распределением Бернулли. Пусть р – вероятность наступления события А
в одном испытании, q = 1 – p – вероятность |
̅ |
|
||||||
. Тогда |
|
|||||||
|
|
1 |
|
|
0, |
x 0, |
|
|
|
X |
0 |
|
x 1, |
|
|||
|
|
|
|
; F (x) q, 0 |
|
|||
|
|
p |
q |
|
|
x 1. |
|
|
|
|
|
|
|
1, |
|
||
Для такой случайной величины Х M (X ) p, |
D(X ) pq. |
|||||||
В нашей задаче |
M (X |
) 0,30; M( X ) |
0,35; M( X ) |
0,40; |
||||
|
|
|
1 |
|
2 |
|
3 |
|
D(X |
) 0,30 0,70 |
0,2100; |
D( X) 0,2275; D( |
X) 0,2400. |
||||
1 |
|
|
|
|
2 |
|
3 |
|
Общее число линий Х, которое потребует вмешательства рабочего, равно сумме Х = Х1 + Х2 + Х3. Поэтому
M (X ) M (X 1) M (X 2) M (X 3) 1,05 , и поскольку величины Х1, Х2
и Х3 – независимы, то D(X ) D(X 1) D(X 2) D(X 3) 0,6775 . Ответ: М(Х) = 1,05; D(X) = 0, 6775.
2.16.Из урны, содержащей 10 белых и 15 чёрных шаров, высыпались какие-то 8 шаров. Сколько в среднем чёрных шаров высыпалось из урны?
2.17.В распоряжении монтёра имеется 10 новых лампочек; каждая из них с вероятностью р = 0,05 имеет дефект. При включении тока дефектная лампочка сразу же перегорает, после чего заменяется дру-
43

гой. Пусть с.в. Х – число лампочек, которые будут испробованы. Построить ряд распределения и найти математическое ожидание с.в.
Замечание. Распределение с.в., характеризующее число попыток до первого наступления успеха, называется геометрическим. Условимся обозначать его G( p) . Число попыток в принципе может быть бесконечным, и ряд распределения имеет вид
Х |
1 |
2 |
… |
n |
… |
Р |
p |
qp |
… |
qn-1p |
… |
Вероятности последовательных значений Х образуют бесконечно убывающую геометрическую прогрессию, чем и объясняется название распределения. Условие нормировки
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
pn |
p qn p |
|
p |
|
1. Если X |
|
G( p), то |
M ( X ) |
. |
||||||||||||||||||||
1 q |
p |
|
|
||||||||||||||||||||||||||
n |
n 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|||||
2.18. |
Задано распределение дискретной с.в. Х: |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Х |
|
-2 |
|
|
-1 |
1 |
|
2 |
|
3 |
|
|
|
|
|
|
|||||||||
|
|
|
|
Р |
0,20 |
0,25 |
0,30 |
0,15 |
0,10 |
|
|
|
|
|
|||||||||||||||
Построить ряд распределений случайных величин: |
|
|
|
||||||||||||||||||||||||||
a) Y X a; |
б) Z a X ; |
|
|
в) W X 2. Вычислить числовые харак- |
|||||||||||||||||||||||||
теристики этих величин и второй начальный момент. |
|
|
|
||||||||||||||||||||||||||
2.19. Задано распределение дискретной с.в. Х: |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
Х |
-3 |
|
|
|
-1 |
|
0 |
|
|
1 |
|
3 |
|
5 |
|
|
|
|
||||||||
|
|
|
Р |
0,05 |
|
0,20 |
|
0,25 |
|
|
0,30 |
|
0,15 |
|
0,05 |
|
|
|
|
||||||||||
Найти распределение с.в.: |
|
a) Y |
|
X |
|
; |
|
б) Z X 3 |
1. |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||
2.20. Автомашина проходит технический осмотр и обслуживание. Число неисправностей, обнаруженных во время техосмотра, распределяется по закону Пуассона с параметром а. Если неисправностей не обнаружено, техническое обслуживание машины продолжается в среднем 2 часа. Если обнаружены одна или две неисправности, то на устранение каждой из них тратится в среднем ещё полчаса. Если обнаружено больше двух неисправностей, то машина ставится на профилактический ремонт, где она находится в среднем 4 часа. Определить закон распределения среднего времени Т обслуживания и ремонта машины и его математическое ожидание М(Т).
44
2.3. Непрерывные случайные величины (н.с.в.)
Случайная величина Х называется непрерывной (н.с.в.), если её значения заполняют некоторый отрезок, а функция распределения
F(x) P( X x)
непрерывна на всей числовой оси. Свойства функции распределения для н.с.в. такие же как и для дискретной с.в. Но в отличие от дискретной с.в. вероятность отдельного значения н.с.в. равна нулю:
P(X c) F(c 0) F(c) 0
(так называемый «парадокс непрерывности»).
При этом существует такая неотрицательная функция ( ) (другое обозначение – ( )), ( ) , называемая плотностью распределе-
ния вероятностей (или просто – «плотность вероятности»), что
x
F (x) P{X x} f (t)dt .
Плотность вероятности обладает следующими свойствами:
1) f (x) 0, |
x ; |
|
|
2) |
f (x)dx 1 (условие |
|
|
нормировки);
3) f (x) F (x) в точках непрерывности плотности вероятности.
Для н.с.в. Х с плотностью вероятности f(x) при a<b
P{a X b} P{a X b} P{a X b} P{a X b}
b
F (b) F (a) f (x)dx.
a
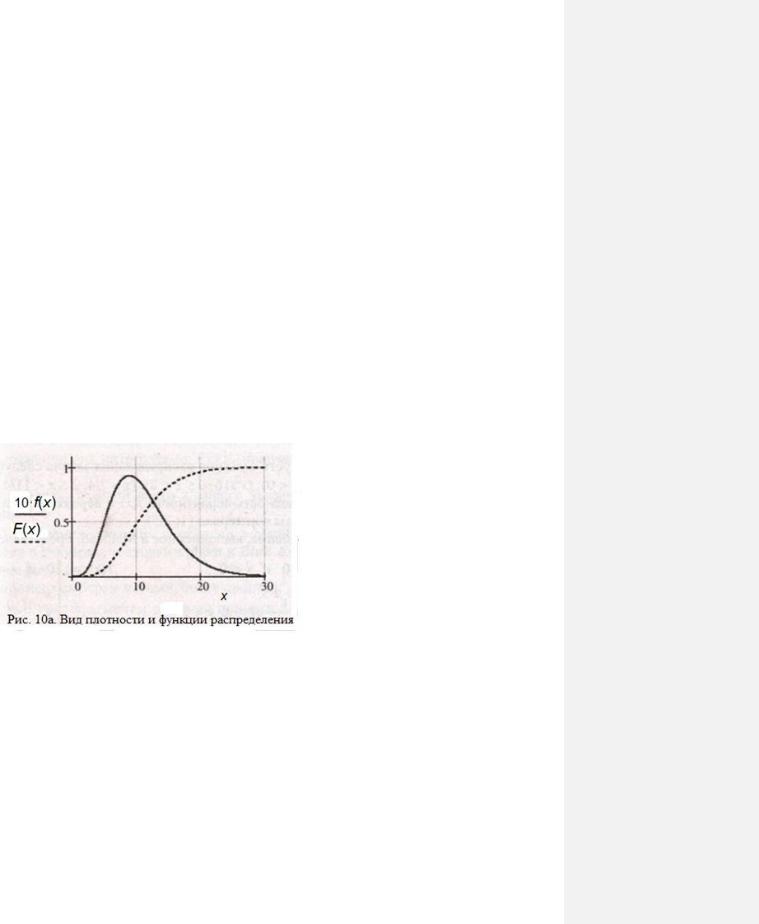
На рисунке 10а приведены типичный вид функции распределения ( ) и плотности распределения ( ) (для наглядности её масштаб
увеличен в 10 раз)
45
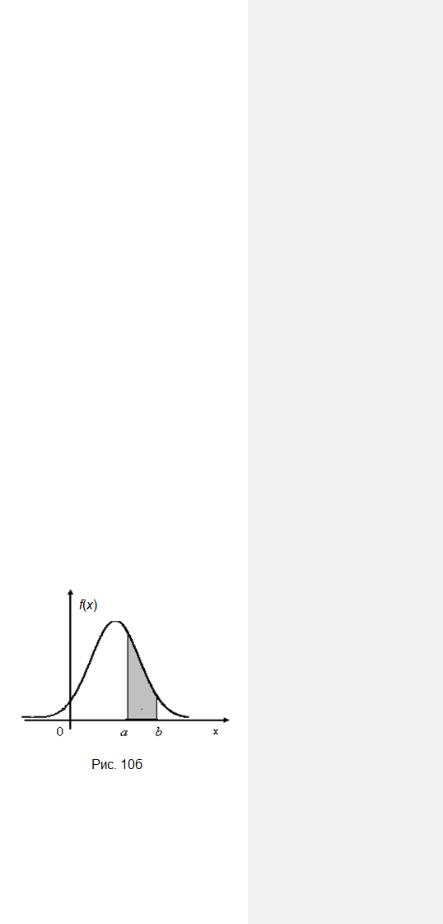
Таким образом, вероятность попадания с.в. в промежуток с концами a и b геометрически можно рассматривать как площадь под кривой плотности вероятности, которая приходится на этот промежуток
(рис. 10б).
Числовые характеристики случайной величины Х с плотностью вероятности f(x) находятся аналогично тому, как они определялись для дискретных с.в., при этом, естественно, суммы заменяются интегралами, а вероятности – плотностью вероятности:
M ( X ) xf (x)dx,
|
|
D( X ) M [( X M ( X ))2 ] (x m)2 f (x)dx |
|
|
|
|
|
M ( X 2 ) [M ( X )]2 |
x2 f (x)dx ( xf (x)dx)2 . |
|
|
Среднее квадратическое отклонение ( X ) определяется форму-
лой (2.4).
Математическое ожидание и дисперсия называются также моментами соответственно первого и второго порядков. В теории вероятностей вводятся также числовые характеристики в виде моментов более высокого порядка. В принципе, совокупность моментов всех порядков эквивалентно заданию функции распределения. Такой точности для описания случайных величин и не требуется, так что на практике ограничиваются меньшим числом моментов. Обычно ограничиваются моментами порядка не выше четвёртого.
Различают два типа моментов – начальные и центральные.
Начальным моментом поряд-
ка к с.в. Х называется число , определяемое по формуле
|
k |
M ( X k ) |
k 0,1,2,.... |
|
|
|
|
|
|
Для дискретной с.в. |
|
k |
xik pi |
|
|
i
Для непрерывной с.в. k xk f (x)dx
46
Центральным моментом к-го порядка с.в. Х называется матема-
тическое ожидание величины ( X mx )k ( X 0 )k :
k M[( X mx )k ].
Соответственно для дискретной и непрерывной величины имеем:
|
(xi mx )k pi ; |
|
k |
k (x mx )k f (x)dx. |
|
|
i |
|
Из этих определений видно, что введённые ранее математическое ожидание и дисперсия связаны с начальными и центральными моментами формулами:
1 M ( X ) mx; 1 0
|
|
|
|
|
|
|
|
2 |
D( X ) 2 |
( X ); |
( X ) |
. |
|
|
|
|
2 |
|
||
Кроме названных величин, используются ещё моменты третьего и четвёртого порядков, которые определяют асимметрию АХ и эксцесс ЕХ , характеризующих форму кривых распределения.
Коэффициент асимметрии определяется формулой
AX M[( X mx )3 ]/ 3 ( X ).
Он характеризует скошенность кривой распределения влево (АХ < 0) или вправо (АХ > 0).
Эксцессом случайной величины называется безразмерный коэффициент
EX {M[( X mx )4 ]/ 4 ( X )} 3
Он характеризует отличие распределения от нормального (см. ниже), для которого ЕХ = 0.
Мода и медиана. Квантили.
Выше названные величины характеризуют вид функции распределения. Модой с.в. называется её наиболее вероятное значение. Медианой называется такое значение хр, для которого вероятности слева и справа от этой точки под кривой плотности вероятности равны –
Важной числовой характеристикой является квантиль, определяющая
47
связь функции распределения с соответствующим значением случайной величины на числовой оси.
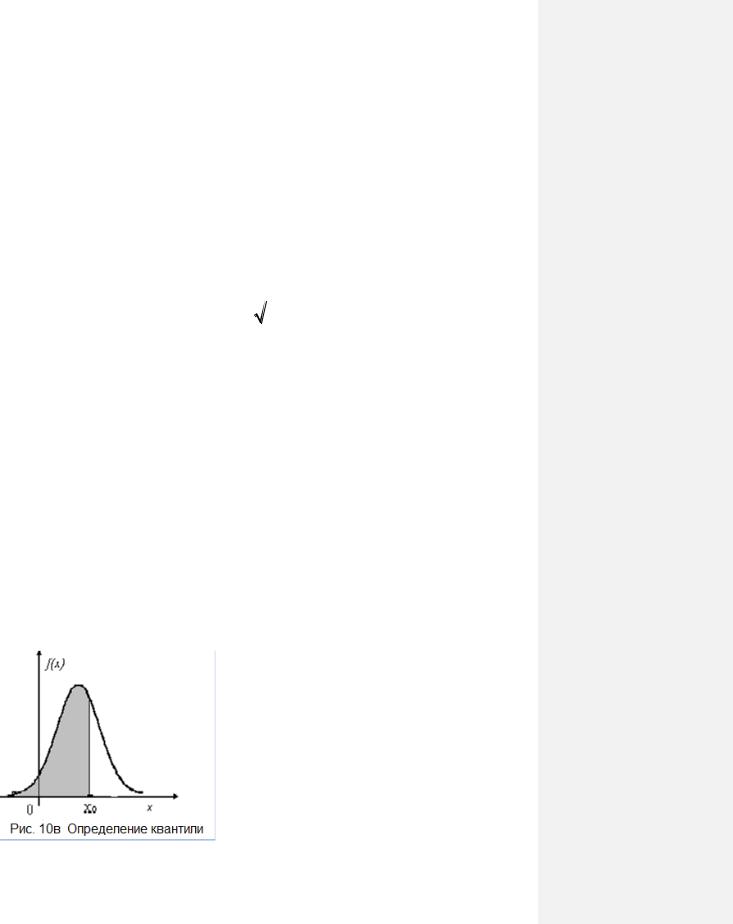
Квантилью порядка р называется такое значение xp случайной величины, для которой
P( X xp ) F(xp ) p
На рисунке 10в квантиль Х0 соответствует F (x0 ) , т.е. заштрихованной площади под кривой плотности вероят-
ности в диапазоне ( , X0 ). Из этого определения следует, что кван-
тиль х0,5 |
медиана, а х0,25 и х0,75 |
носят название нижней и верхней |
|||||||||
квартили. |
|
|
|
|
|
|
|
|
|
|
|
Кроме того, полезно знать, как связаны плотности вероятности |
|||||||||||
fX (x) и |
faX b (x) случайных величин Х и aX +b при a ≠ 0: |
|
|||||||||
|
faX b (x) |
|
1 |
|
|
x b |
|
||||
|
|
|
|
|
|
fX |
|
|
. |
(2.8) |
|
|
|
|
a |
|
|
|
|
||||
|
|
|
|||||||||
|
|
|
|
|
|
|
a |
|
|||
Пример
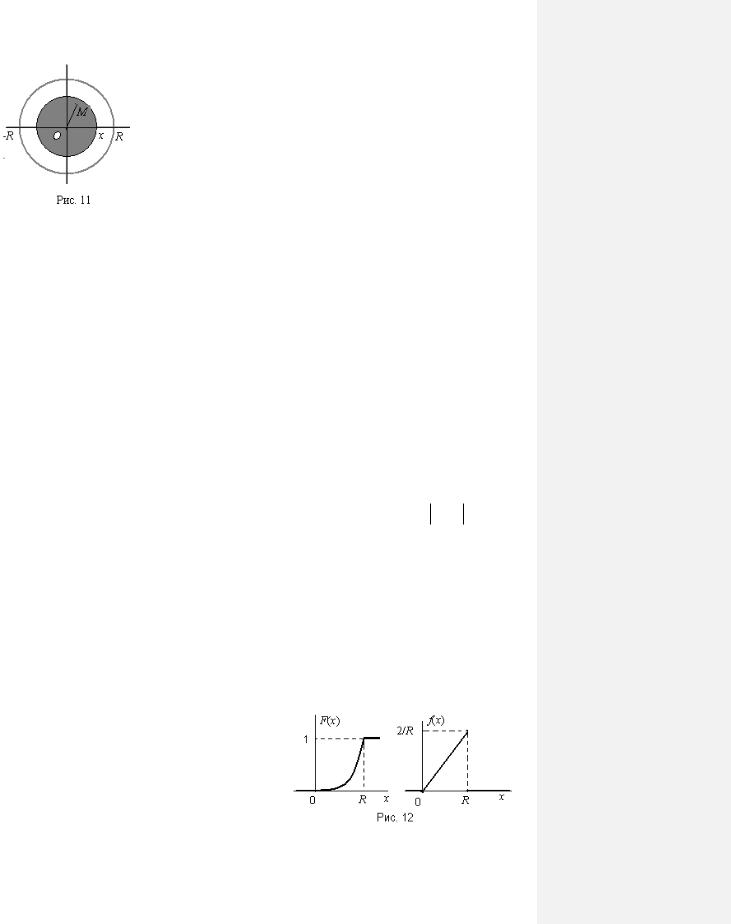
Вкруге радиуса R с центром в точке О наугад выбирается точка
М. Найти функцию распределения, плотность вероятности, математическое ожидание и дисперсию случайной величины Х , равной рас-
стоянию между точками М и О (рис. 11).
Решение. При 0 x R вероятность P( X x) P( OM x) равна отношению площади круга радиуса х к площади круга радиуса
R: |
P( |
|
OM |
|
x) |
x2 |
|
x2 |
. |
|
|
||||||||
|
|
R2 |
R2 |
||||||
|
|
|
|
|
|
|
|
Тогда функция распределения с.в. Х равна
Соответствующая плотность вероятности f(x) получается дифференцированием функции распределения F(x). В результате получаем
|
|
0, |
x 0, |
|
|
|
|
|
|
x2 |
|
|||
F (x) |
|
|
, |
0 x R, |
|
2 |
|||
R |
|
|
x R. |
|
|
1, |
|||
|
|
|
|
|
48

2x |
|
|
|
0 x R, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
f (x) R2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
x |
0 и x R . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Графики обеих функций приведены на рис. 12. |
|
|
||||||||||||||||||||
Числовые характеристики данной с.в. Х вычисляются по опреде- |
||||||||||||||||||||||
лению: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
2x |
|
|
2 |
|
|
|
|||||
|
|
|
|
|
M ( X ) |
xf (x)dx x |
|
dx |
R; |
|
|
|||||||||||
|
|
|
|
|
|
2 |
3 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
R |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
R |
2x |
|
|
|
|
R |
2 |
|
|
|
|
|
|
|
M ( X 2 ) x2 f (x)dx x2 |
dx |
|
|
; |
|
|
|
|
|
|||||||||||||
2 |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
0 |
R |
|
|
2 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
D( X ) M ( X 2 ) (M ( X ))2 |
R2 |
/ 2 4R2 / 9 R2 /18. |
|
|
||||||||||||||||||
Задачи |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2.21. Пусть |
|
( |
) – плотность вероятности. Найти значение входящей |
|||||||||||||||||||
в определение р(х) постоянной С: |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1) p(x) |
|
|
0, |
|
x 0, |
0; |
2) p(x) |
|
|
C |
|
a . |
||||||||||
Ce x , |
x 0; |
|
|
, |
||||||||||||||||||
1 (x a)2 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.22. Задана плотность вероятности с.в. : |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
2 |
|
0 x 1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) ax |
|
, |
Найти: 1) постоянную a; 2) F(x); |
3) чис- |
||||||||||||||||||
|
0, |
|
x 0, x 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ловые характеристики с.в.; 4) |
P( 1/ 2). |
|
|
|
|
|
||||||||||||||||
2.23. Существует ли значение С такое, что функция f(x) служит плотностью вероятности? Если существует, то указать его и вычислить соответствующие математическое ожидание и дисперсию:
C, |
|
0 x 5, |
1) f (x) |
x 0, x 5; |
|
0, |
||
|
2 x |
, x 0, |
3) f (x) Ce |
|
|
0, |
|
x 0; |
C(1 |
|
x |
|
), |
|
x |
|
1, |
|||||
|
|
|
|
||||||||||
2) f (x) |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
1; |
|||||||
0, |
|
|
|
|
|
x |
|||||||
|
|
|
|
|
|||||||||
4) f (x) Ce |
|
x |
|
, |
|
x . |
|||||||
|
|
|
|||||||||||
2.24. Дана плотность вероятности непрерывной с.в.
a cos x, |
/ 2 x / 2, |
||||
f (x) |
0, |
|
x |
|
/ 2. |
|
|
||||
|
|
|
|||
49
Найти постоянную a, |
вычислить P |
|
X |
|
/ 4 , mx , Dx . |
|||
|
|
|||||||
2.25. Найти |
( ) |
( |
) по заданной функции распределения: |
|||||
|
|
0, |
|
x 0, |
||||
F (x) |
sin2 x, |
0 x / 2, |
||||||
|
|
|
|
|
|
|
|
|
|
|
1, |
x / 2. |
|||||
|
|
|||||||
2.26. Дана функция распределения непрерывной с.в.:
|
0, |
x 1, |
|
|
1 x 2, |
F (x) ax b, |
||
|
1, |
x 2. |
|
||
Найти: 1) a, b; 2) f(x); 3) P(0<X<1/2); 4) построить графики f (x), F(x); 5) вычислить числовые харак-
теристики с.в. Х.
2.3.1. Примеры непрерывных распределений
O |
а |
b |
x |
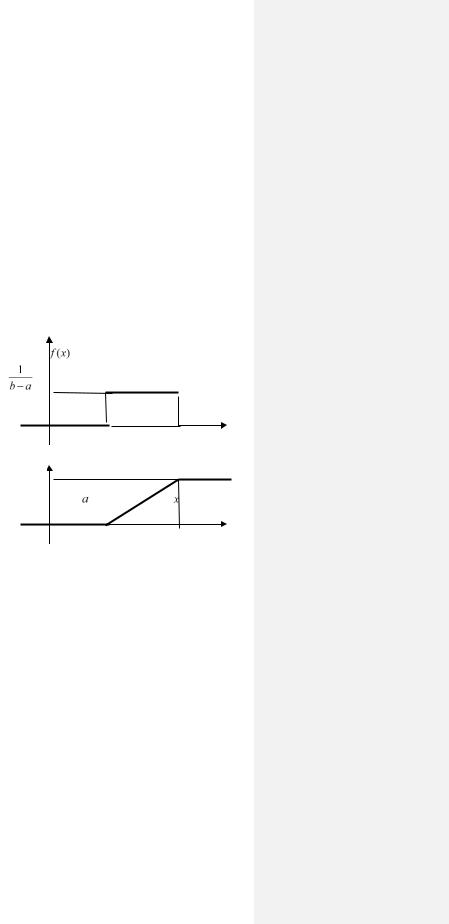
1) Равномерное распределение
R( )
F(x)
1
Рассмотрим с.в. Х, которая с
одинаковой вероятностью может |
O |
b |
|
|
|
||
принимать любое значение в ин- |
|
Рис. 13 |
|
тервале (a, b). Плотность вероятно- |
|
|
|
сти такой случайной величины можно задать в виде: |
|||
C, |
a x b, |
|
|
f (x) |
x a, x b. |
|
|
0, |
|
|
|
где С – некоторая постоянная, которая определяется из условия нор-
мировки C = 1/(b –a).
Используя формулу, связывающую плотность вероятности с функцией распределения данной случайной величины, вычислим по-
|
x |
следнюю: При x a |
F (x) 0 dt 0, |
|
|
50
